
Теория вероятности
Симметричная монета
Выполнила
Шмидт Наталья Александровна

Монета
Монета (лат. moneta ) — денежный знак, изготовленный из металла либо другого материала определённой формы, веса и достоинства. Кроме полноценных монет выпускаются разменные, коллекционные, памятные и инвестиционные монеты. Чаще всего монеты изготавливаются из металла методом чеканки и имеют форму правильного круга.
Почти каждая монета имеет лицевую сторону — аверс, и оборотную сторону — реверс.

« Аве́рс »
Аве́рс (фр. avers , лат. adversus — «обращённый лицом») — лицевая, главная сторона монеты.
Общепринятым в современных монетных каталогах считается определение аверса по следующим признакам по убыванию важности:
- Портрет главы государства, монарха, монетного сеньора или другого обладателя монетной регалии.
- Государственный герб, эмблема и т. п. При этом, если на обеих сторонах монеты изображены гербы, то за аверс принимается та, на которой изображён герб, более высокий по рангу и положению. Например, на монетах португальских колоний на аверсе обычно изображался герб Португалии, а на реверсе — герб колонии.
- Легенда с названием страны, территории.
- Легенда с именем обладателя монетной регалии, либо обозначе-ние банка-эмитента.

« Аве́рс »
В случаях, когда изображение монеты не несёт ни портрета монарха, ни названия страны или обозначения банка эмитента, ни государственного герба - аверсом принято считать сторону, противоположную стороне, на которой изображён номинал монеты.
Орёл (не тождествен аверсу ) — в дореволюционной России так именовалась в обиходе сторона монеты с изображением государственного герба. Первые общегосударственные монеты мелких номиналов, появившиеся после денежной реформы Петра I, несли на аверсе изображение двуглавого орла.

« Ре́верс »
Ре́верс (лат. revertor — «поворачиваю назад») — оборотная сторона монеты, противоположная аверсу.
Реверсом принято считать сторону с номиналом монеты, хотя бывает, когда сторона с номиналом является аверсом. Реверс не тождественен решке.

Монета с точки зрения теории вероятностей лишена многих качеств настоящей монеты. У неё нет цвета, размера, веса и достоинства. Она не сделана ни из какого материала и не может служить платежным средством. Математическая монета имеет только две стороны, одна из которых называется "орел", а другая — "решка". Монету бросают, и она падает одной из сторон вверх.
- Математическая монета считается симметричной . Это означает, что брошенная на стол монета имеет равные шансы выпасть "орлом" или "решкой" . При этом подразумевается, что никакой другой исход бросания монеты невозможен, — она не может потеряться, закатившись в угол, и, тем более, не может "встать на ребро".
- Настоящая металлическая монета служит лишь иллюстрацией для математической монеты. Настоящая монета может быть немного вогнутой, может иметь другие дефекты, которые влияют на результаты бросания.

Задачи на подбрасывание монет считаются довольно сложными. Тем не менее, существует как минимум два принципиально различных метода решения:
- Метод перебора комбинаций — стандартный алгоритм. Выписываются все комбинации орлов и решек, после чего выбираются нужные;
- Специальная формула вероятности — стандартное определение вероятности, специально переписанное так, чтобы было удобно работать с монетами.
При решении задачи B6 для подготовки к ЕГЭ по математике надо знать оба метода.

Метод перебора комбинаций
Состоит из трех шагов:
- Выписываем все возможные комбинации орлов и решек. Например: ОР, РО, ОО, РР. Число таких комбинаций — это n ;
- Среди полученных комбинаций отмечаем те, которые требуются по условию задачи. Считаем отмеченные комбинации — получаем число k ;
- Осталось найти вероятность Р .
Вероятностью Р наступления случайного события А называется отношение k к n, где n – это число всех возможных исходов эксперимента, а k – это число всех благоприятных исходов. P(A) = k /n, где k - число благоприятствующих событию A исходов, n – число всех элементарных равновозможных исходов.
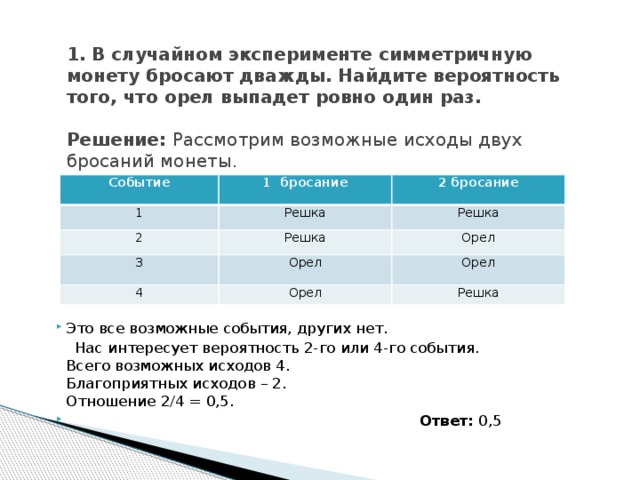
1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Решение: Рассмотрим возможные исходы двух бросаний монеты.
Событие
1 бросание
1
Решка
2
2 бросание
Решка
3
Решка
Орел
Орел
4
Орел
Орел
Решка
- Это все возможные события, других нет.
Нас интересует вероятность 2-го или 4-го события. Всего возможных исходов 4. Благоприятных иcходов – 2. Отношение 2/4 = 0,5.
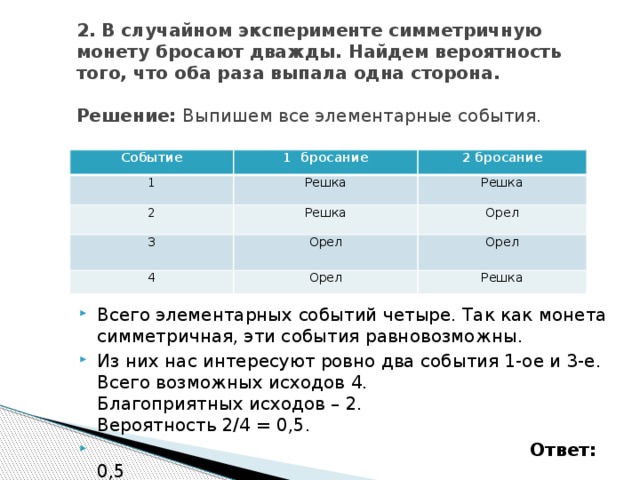
2. В случайном эксперименте симметричную монету бросают дважды. Найдем вероятность того, что оба раза выпала одна сторона. Решение: Выпишем все элементарные события.
Событие
1 бросание
1
Решка
2
2 бросание
Решка
Решка
3
Орел
Орел
4
Орел
Орел
Решка
- Всего элементарных событий четыре. Так как монета симметричная, эти события равновозможны.
- Из них нас интересуют ровно два события 1-ое и 3-е. Всего возможных исходов 4. Благоприятных иcходов – 2. Вероятность 2/4 = 0,5.
- Ответ: 0,5
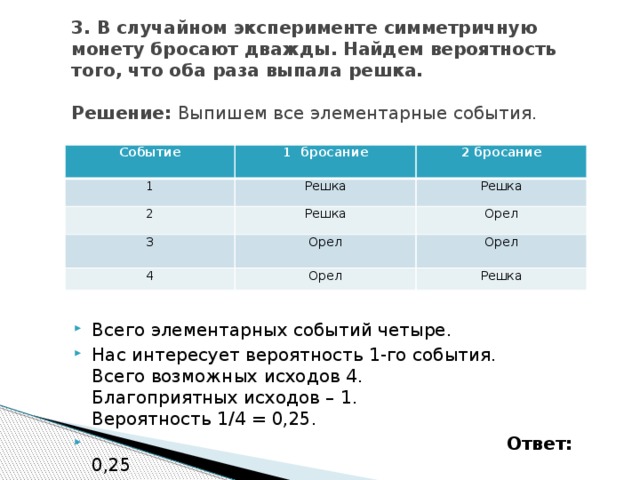
3. В случайном эксперименте симметричную монету бросают дважды. Найдем вероятность того, что оба раза выпала решка. Решение: Выпишем все элементарные события.
Событие
1 бросание
1
Решка
2
2 бросание
Решка
Решка
3
Орел
Орел
4
Орел
Орел
Решка
- Всего элементарных событий четыре.
- Нас интересует вероятность 1-го события. Всего возможных исходов 4. Благоприятных иcходов – 1. Вероятность 1/4 = 0,25.
- Ответ: 0,25
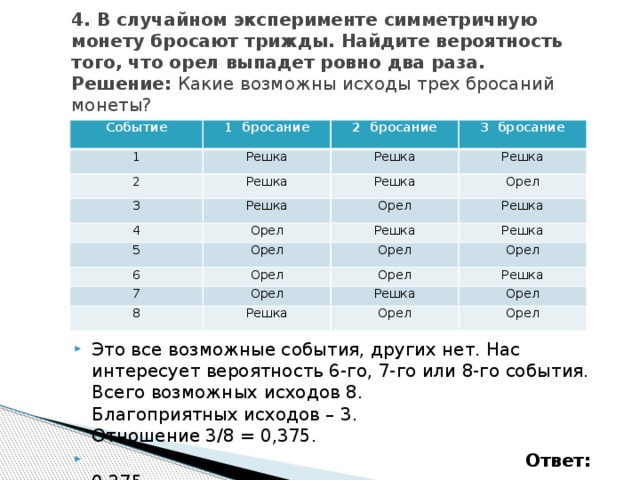
4. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза. Решение: Какие возможны исходы трех бросаний монеты?
Событие
1 бросание
1
Решка
2 бросание
2
3
3 бросание
Решка
Решка
Решка
Решка
4
Решка
Орел
5
Орел
Орел
Решка
Орел
6
Решка
Решка
Орел
Орел
7
Орел
Орел
Орел
8
Решка
Решка
Решка
Орел
Орел
Орел
- Это все возможные события, других нет. Нас интересует вероятность 6-го, 7-го или 8-го события. Всего возможных исходов 8. Благоприятных иcходов – 3. Отношение 3/8 = 0,375.
- Ответ: 0,375
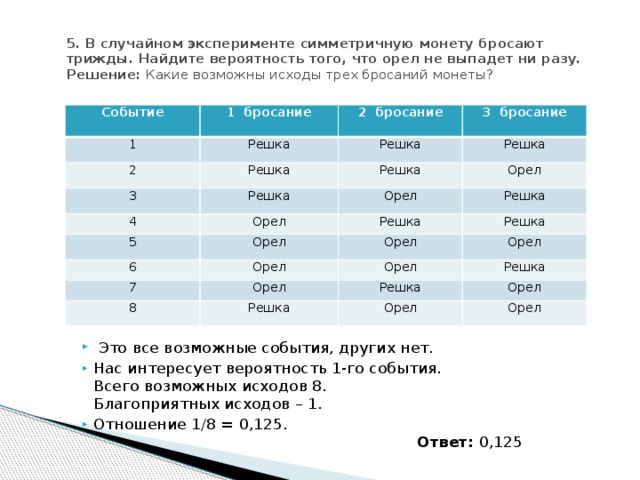
5. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу. Решение: Какие возможны исходы трех бросаний монеты?
Событие
1 бросание
1
Решка
2 бросание
2
3
3 бросание
Решка
Решка
Решка
Решка
4
Решка
Орел
5
Орел
Орел
Решка
Орел
6
Решка
Решка
Орел
Орел
7
Орел
Орел
Орел
8
Решка
Решка
Решка
Орел
Орел
Орел
- Это все возможные события, других нет.
- Нас интересует вероятность 1-го события. Всего возможных исходов 8. Благоприятных иcходов – 1.
- Отношение 1/8 = 0,125. Ответ: 0,125
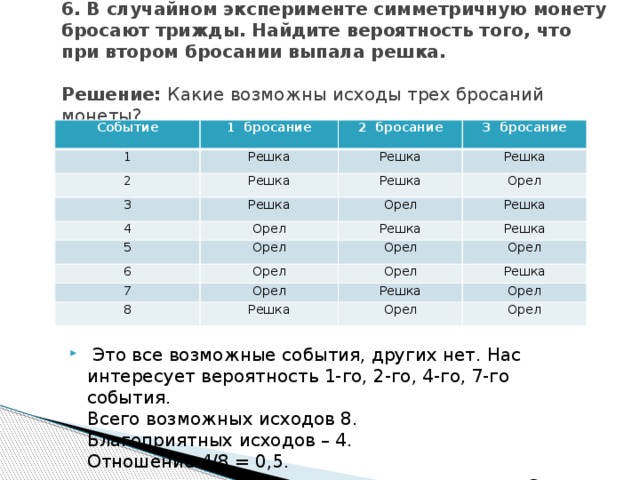
6. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что при втором бросании выпала решка. Решение: Какие возможны исходы трех бросаний монеты?
Событие
1 бросание
1
Решка
2 бросание
2
3
3 бросание
Решка
Решка
Решка
Решка
4
Решка
Орел
Орел
Орел
5
Решка
Орел
Решка
6
Орел
7
Решка
Орел
Орел
Орел
8
Орел
Решка
Решка
Решка
Орел
Орел
Орел
- Это все возможные события, других нет. Нас интересует вероятность 1-го, 2-го, 4-го, 7-го события. Всего возможных исходов 8. Благоприятных иcходов – 4. Отношение 4/8 = 0,5.
- Ответ: 0,5
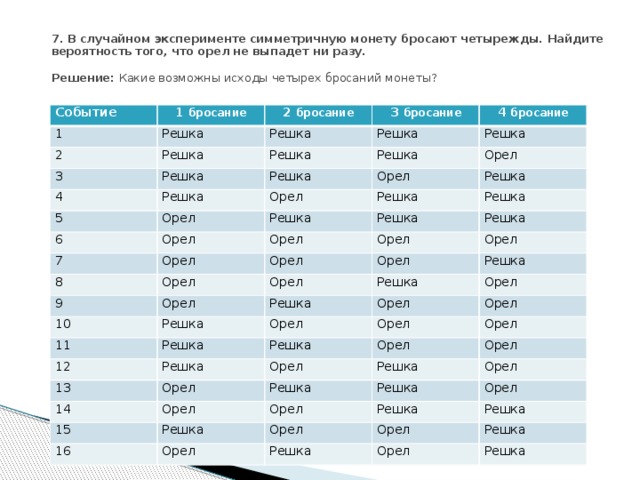
7. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу. Решение: Какие возможны исходы четырех бросаний монеты?
Событие
1 бросание
1
2 бросание
2
Решка
Решка
3 бросание
Решка
3
Решка
4
Решка
4 бросание
Решка
Решка
Решка
5
Решка
Решка
Орел
Орел
Орел
Орел
6
Решка
Орел
Решка
7
Решка
8
Орел
Решка
Решка
Орел
Орел
Орел
Орел
Решка
9
Орел
Орел
Орел
10
Орел
Решка
Решка
Решка
Решка
11
Орел
12
Орел
Решка
Орел
Орел
Решка
13
Орел
Решка
Орел
Орел
Орел
Орел
14
Решка
Орел
Орел
Решка
15
Решка
Решка
Орел
Орел
16
Решка
Орел
Орел
Орел
Орел
Решка
Решка
Решка
Орел
Решка

- Это все возможные события, других нет.
Нас интересует вероятность 1-го события. Всего возможных исходов 16. Благоприятных иcходов – 1. Отношение 1/16 = 0,0625 Ответ: 0,0625
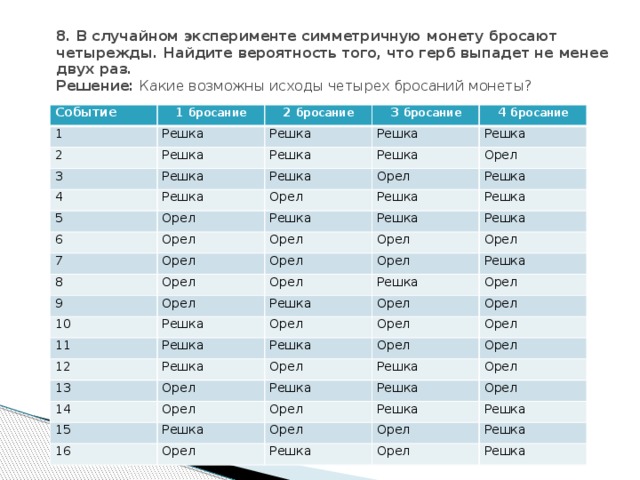
8. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что герб выпадет не менее двух раз. Решение: Какие возможны исходы четырех бросаний монеты?
Событие
1 бросание
1
2 бросание
2
Решка
Решка
3 бросание
3
Решка
Решка
Решка
4 бросание
Решка
4
Решка
Решка
Решка
Решка
5
6
Орел
Орел
Орел
Орел
Решка
Орел
Решка
Решка
7
8
Орел
Решка
Решка
Орел
Орел
Орел
Решка
Орел
9
10
Орел
Орел
Орел
Орел
Решка
Решка
11
Решка
Решка
12
Решка
Орел
Орел
Орел
Орел
Решка
13
Решка
Орел
Орел
Орел
14
Орел
Орел
Орел
Решка
Решка
Орел
15
Решка
Орел
Орел
Решка
16
Решка
Орел
Орел
Орел
Орел
Решка
Решка
Решка
Орел
Решка

- Это все возможные события, других нет.
Нас интересует вероятность с 6-го по 16-е события. Всего возможных исходов 16. Благоприятных иcходов – 11. Отношение 11/16 = 0,6875
Ответ: 0, 6875

- К сожалению, этот способ работает лишь для малого количества бросков. Потому что с каждым новым броском число комбинаций удваивается. Для 2 монет придется выписать всего 4 комбинации. Для 3 монет их уже 8, для 4-16, для 5-32, а для 10-1024 различных комбинаций. Вы уверены, что сможете выписать их без единой ошибки? Поэтому давайте рассмотрим второй способ решения.

Специальная формула вероятности
Итак, в задачах с монетами есть собственная формула вероятности.
- Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле:
Р = С n k / 2 n
- Где С n k — число сочетаний из n элементов по k ,
которое считается по формуле:
С n k =n!/k!(n-k)!
- Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи.
Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.

9. В случайном эксперименте симметричную монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.
- Решение:
- Выписываем числа n и k .
Поскольку монету бросают 3 раза, n = 3.
А поскольку решек быть не должно, k = 0.
Осталось подставить числа n и k в формулу:
- Р= С 3 0 / 2 3
- С 3 0 = 3!/0!(3-0)! =1
- 2 3 =8
- Р = 1/8 = 0,125

10. В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.
- Решение:
- По условию задачи, всего бросков было n = 4.
Требуемое число орлов: k =3.
Подставляем n и k в формулу:
- Р= С 4 3 / 2 4
- С 4 3 =4!/3!(4-3)! = 4
- 2 4 = 16
- Р = 4/16 = 0,25
- С тем же успехом можно считать число решек:
k = 4 − 3 = 1. Ответ будет таким же.

УСПЕХА!


 Получите свидетельство
Получите свидетельство Вход
Вход



































 Презентация по математике "Теория вероятности. Симметричная монета" (0.18 MB)
Презентация по математике "Теория вероятности. Симметричная монета" (0.18 MB)
 0
0 2746
2746 57
57 Нравится
0
Нравится
0


