Учитель математики МАОУ Улу-Юльской СОШ ОлейВ.И.
Обобщение и систематизация знаний
по теме «Решение показательных уравнений и неравенств» в 11 профильном классе
Цели урока:
Обучающие:
повторить свойства показательной функции, применение свойств при решении показательных уравнений и неравенств;
решение комбинированных уравнений и неравенств, сводящихся к решению тригонометрических, дробно-рациональных уравнений и неравенств, неравенств с модулем;
повторить возможные случаи потери корней при решении уравнений, а также случаи приобретения посторонних корней.
Развивающие:
развивать навыки самостоятельного применения знаний в знакомой и измененной ситуации;
учить анализировать, выделять главное, доказывать и опровергать логические выводы.
Воспитательные:
формирование нравственных качеств, аккуратности, дисциплинированности, чувства собственного достоинства, ответственного отношения к достижению цели;
формировать навыки коллективного труда.
Тип урока: урок обобщения и систематизации знаний.
План урока:
Организационный момент.
Повторение и актуализация опорных знаний.
Тест по проверке умения решать простейшие показательные уравнения и неравенства
Решение комбинированных уравнений и неравенств.
Подведение итогов. Задание на дом.
Проводится в форме фронтальной работы с классом.
Задания устного опроса можно разделить на две части: повторение теоретического материала и умения применять эти знания при выполнении различных заданий.
Какую функцию называют монотонной?
Какую функцию называют возрастающей? Какую функцию называют убывающей?
Какая функция называется показательной? Каковы область определения и множество значений показательной функции?
Какую показательную функцию называют возрастающей? (убывающей?)
Важен ли характер монотонности показательной функции при решении уравнений?
Как используется характер монотонности при решении показательных неравенств?
Устные упражнения:
Какие из перечисленных показательных функций являются возрастающими, и какие убывающими:
 ;
; 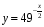 ;
; 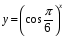 ;
;
Сравните:
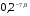 и
и 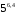 ;
; 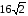 и
и 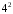 ;
; 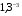 и
и 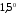 .
.
Решите уравнения:
а) 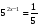 б) 2х-2 = -2 в)
б) 2х-2 = -2 в) 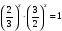
Решите неравенства:
а) 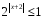 б)
б) 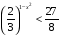 в)
в) 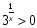
3. Тест по проверке умения решать простейшие показательные уравнения и неравенства
Учащиеся выполняют тест на подготовленных бланках, в таблице ответов ниже номера задания записывают цифру, которая соответствует правильному ответу.
Вариант 1
1) Решите уравнение: 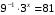
1) 6 2) 2 3) 5 4) 1
2) Решите неравенство: 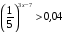
1) 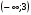 2)
2) 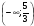 3)
3) 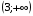 4)
4) 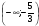

3) Решите уравнение: 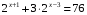
1) 4 2)5 3) 3 4) 6
4) Решите неравенство: 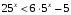
1) (1;5) 2) (1;+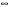 ) 3)
) 3)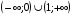 4) (0;1)
4) (0;1)
1) Решите уравнение:
1) 6 2) 2 3) 5 4) 1
2) Решите неравенство:
1) -3 2) [7;+∞) 3) (-∞;-1] 4) [1;+∞)
3) Решите уравнение:
1) 2) -3 3) -
4) 3
4) Решите неравенство:
1) (0;1) 2) (-∞;1) 3)
4) (1;2)
ученики по порядку называют задание и дают на него ответ с обоснованием. Во время проверки ученики корректируют свои знания по этой теме. По окончании проверки каждый выставляет себе оценку и сдает бланк учителю.
Каждое задание решает группа учащихся. Затем один из группы записывает решение на доске и поясняет его.
1).
Решение:
Преобразуем показатели степеней:
геометрическая прогрессия,
,
Получим:
,
,
Ответ:
2).
Решение:
Перейдем к одному основанию и воспользуемся свойствами степеней:
Из монотонности показательной функции следует:
,
Решением системы является: х = 9
Ответ: 9
3).

Решение:
,

Пусть
Тогда
Ответ:
4).
Решение:
Перейдем к одному основанию и воспользуемся формулами тригонометрии:
Пусть , тогда уравнение примет вид
Ответ:
5).
Решение:
Воспользуемся условием равносильности:
Так как , то данное неравенство равносильно системе:
Ответ:
Выводы, оценки.
Решить уравнения и неравенства:
а) , б)
в*)

 Получите свидетельство
Получите свидетельство Вход
Вход












 Обобщение и систематизация знаний по теме «Решение показательных уравнений и неравенств» в 11 профильном классе (131.84 KB)
Обобщение и систематизация знаний по теме «Решение показательных уравнений и неравенств» в 11 профильном классе (131.84 KB)
 0
0 657
657 77
77 Нравится
0
Нравится
0


