Государственное бюджетное профессиональное образовательное учреждение
Московской области «Подольский колледж имени А.В. Никулина»
План-сценарий урока
по дисциплине «ЕН Математика»
по теме: «Метод прогонки»
для студентов II курса
15.02.15 Технология металлообрабатывающего производства
Преподаватель первой квалификационной категории
Носова Оксана Васильевна
2020
Специальность: 15.02.15 Технология металлообрабатывающего производства
Дисциплина: ЕН Математика
Тема: Метод прогонки.
Цель: изучить точный метод решения систем линейных алгебраических уравнений — метод прогонки для решения систем линейных уравнений с трехдиагональными матрицами коэффициентов.
Задачи:
образовательные:
формирование представлений о системах линейных уравнений с трехдиагональной структурой и методе прогонки,
формирование умений применять знания при решении задач;
развивающие:
способствовать развитию умений обучающихся обобщать полученные знания, проводить анализ, сравнение, делать необходимые выводы;
способствовать развитию логического мышления;
способствовать развитию вычислительных навыков при решении задач по специальности;
воспитательные:
способствовать овладению обучающимися необходимыми навыками самостоятельной учебной деятельности, формирование познавательной активности и умения принимать решения и отвечать за принятые решения.
Тип урока: урок теоретического обучения
Методы:
1) словесные (лекция);
2) наглядные (мультимедийная презентация, опорный конспект);
3) практические (решение задач).
План
1.Вступление
2.Основная часть
-Теоретический материал
-Решение систем линейных уравнений
3.Итог
План-сценарий
1.Вступление
Приветствие. Раздача опорных конспектов
Учитель:
На прошлом занятии мы рассмотрели решение СЛАУ с помощью правила Крамера. Выяснили, что не смотря на свое изящество и простоту, он редко применяется в вычислительной практике решения систем.
Почему? (ответы обучющихся)
Верно. Так, например, если в системе 10 уравнений, то сколько требуется вычислить определителей? (ответы обучющихся)
Верно. Если учесть, что в системах, связанных с реальными практическими задачами, количество неизвестных бывает весьма большим, то станет понятно, что метод решения по правилу Крамера для таких систем, скорее всего окажется неприемлемым.
2.Основная часть
-Теоретический материал
На этом и следующих занятиях мы продолжим изучать методы решения СЛАУ. И сегодня мы познакомимся с одним из методов, который реально используется в вычислительной практике. Этот метод находит широкое применение по двум причинам. Во-первых, он прост и эффективен; во-вторых, системы уравнений, к которым он применим, довольно часто встречаются в задачах математического моделирования. Этот метод называется методом прогонки.
И немного из истории решения СЛАУ нам расскажет _______________________(ФИ).
Задача остальных – при прослушивании сообщения, выяснить, для каких матриц применим метод прогонки.
(сообщение студента) (3 – 4) мин
Итак, для каких же матриц применим метод прогонки.
Верно, для трехдиагональных мартиц.
Во многих задачах матрицы коэффициентов системы линейных алгебраических уравнений являются слабозаполненными. Если ненулевые элементы матрицы коэффициентов расположены только на главной диагонали и на нескольких побочных диагоналях, то такие матрицы называют матрицами ленточной структуры. Рассмотрим частный случай матрицы коэффициентов ленточной структуры — матрицу с трехдиагональной структурой, которая имеет вид:
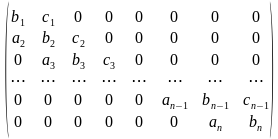 (1)
(1)
и соответствующую ей систему линейных алгебраических уравнений:
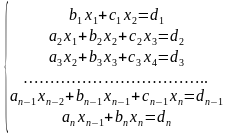
Для решения систем линейных алгебраических уравнений с трехдиагональной матрицей был разработан метод прогонки – метод последовательного исключения неизвестных,состоящий из двух этапов: этапа прямой прогонки, основанного на вычислении прогоночных коэффициентов
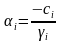 (
(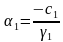 )
)
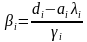 (
(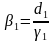 )
)
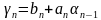 (
(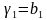 )
)
и этапа обратной прогонки, основанного на использовании прогоночных коэффициентов для нахождения неизвестных, начиная с n-го неизвестного
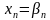 , а затем
, а затем
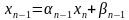 ,
,
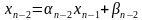 ,…,
,…,
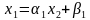 .
.
Условия на коэффициенты системы (1), обеспечивающие успешное нахождение всех неизвестных (ни один из знаменателей 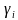 не обращается в нуль), выглядят так:
не обращается в нуль), выглядят так:
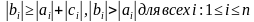 .
.
Это условие называют условием диагонального преобладания. Имеется ввиду, что модули элементов, стоящих на главных диагоналях, не меньше суммы модулей остальных элементов строки матрицы системы.
-Решение систем линейных уравнений
Задача 1. Методом прогонки решить систему линейных алгебраических уравнений (условие есть на опорном конспекте)
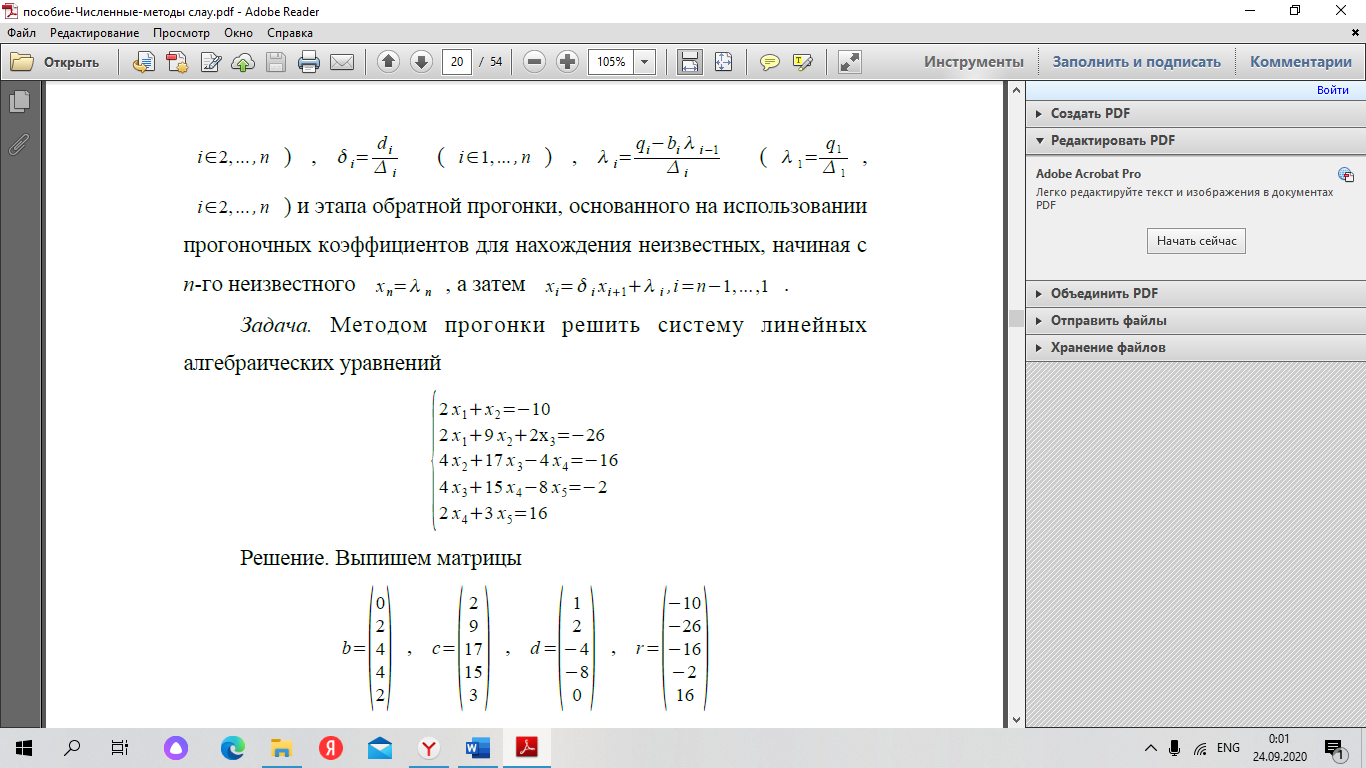
Решение. Запишем коэффициенты в матричном виде
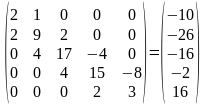
Для удобства выпишем матрицы
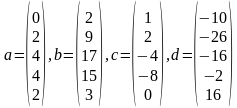
Прямая прогонка. Прямую прогонку осуществляем вычислением пргоночных коэффициентов по приведенным ранее формулам
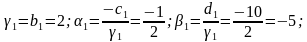
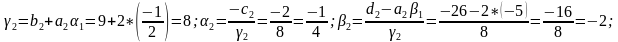
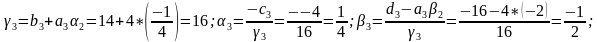
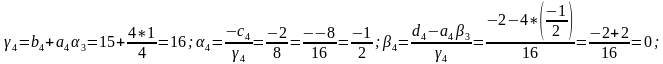
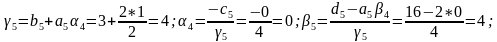
Обратная прогонка. Найдем решение системы линейных алгебраических уравнений
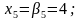
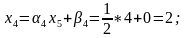
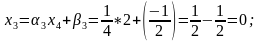
Проверка найденных решений (подставить в уравнения системы)
Ответ:
Задача 2.
Методом прогонки решить систему линейных алгебраических уравнений – один у доски, другие с места («хорошисты» - решают самостоятельно, «троешникам»- раздать карточки с расписанными формулами)
3.Итог
Подведем итог нашего занятия.
Перед вами матрица. Кстати, какая это матрица? (ответы обучающихся)
Под каждым ненулевым элементом матрицы скрыт вопрос или предложение, которое необходимо продолжить. Вы выбираете элемент матрицы и отвечаете на соответствующий вопрос (студенты по очереди выбирают вопросы)
3 – Сегодня на уроке я научился…
1 – Мне было сложно (не сложно) …
2 – Трехдиагональной матрицей называется…
-1 – В чем заключается метод прогонки?
5 – Материал урока мне был … (понятен/непонятен, интересен/ неинтересен).
Домашнее задание. Решить систему методом Крамера и методом прогонки.
Приложение
Опорный конспект
Тема: _______________________________________________________
Матрица с трехдиагональной структурой:
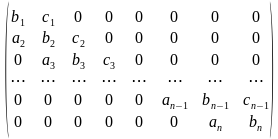 (1)
(1)
Соответствующая ей система линейных алгебраических уравнений:
Алгоритм метода прогонки:
1.Прямая прогонка (вычисление прогоночных коэффициентов)
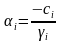 (
(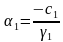 )
)
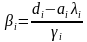 (
(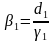 )
)
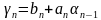 (
(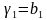 )
)
2.Обратная прогонка (нахождение неизвестных)
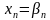 ,
,
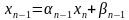 ,
,
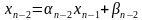 ,…,
,…,
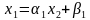 .
.
Задание1.
Задача 1. Методом прогонки решить систему линейных алгебраических уравнений (условие есть на опорном конспекте)

Решение. Запишем коэффициенты в матричном виде
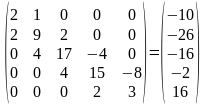
Для удобства выпишем матрицы
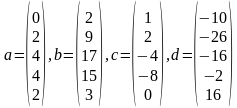

 Получите свидетельство
Получите свидетельство Вход
Вход











 "Метод прогонки" (193.87 KB)
"Метод прогонки" (193.87 KB)
 0
0 645
645 0
0 Нравится
0
Нравится
0


