Государственное учреждение образования
«Лунинская средняя школа»
ОПИСАНИЕ ОПЫТА ПЕДАГОГИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ
«Математические диктанты
и их роль в учебном процессе»
Левшиц Регина Яковлевна,
учитель математики
+ 375 29 9756817;
e-mail: [email protected]
Актуальность опыта
За последние годы учителя математики провели и проводят большую работу по совершенствованию методики организации учебных занятий. Как известно, отказ от шаблонной схемы урока позволил учителю сделать урок более продуктивным, активизировать учащихся, улучшить индивидуальную работу в процессе обучения.
Работая учителем математики, я увидела, что достаточно большие сложности у учащихся вызывает восприятие информации на слух. Поэтому, я пришла к выводу, что одной из важнейших задач в обучении является формирование у детей умения получать информацию на слух, запоминать на слух, обрабатывать и преобразовывать информацию. Из имеющихся в нашем распоряжении органов чувств, воспринимающих информацию, слуховой орган занимает второе место после зрительного, поэтому развивать его возможности у детей крайне важно. Использование математических диктантов помогает в решении вышеуказанных задач.
Математические диктанты проводятся с двумя целями. Прежде всего, они помогают контролировать знания, умения и навыки учащихся. Проанализировав диктанты, учитель получает достаточно подробную информацию об уровне усвоения пройденного как отдельными учащимися, так и классом в целом. Это позволяет оперативно устранять пробелы в подготовке учащихся. Однако ещё более важно то, что математические диктанты играют обучающую роль. Выслушав фразу диктанта, учащиеся выполняют определенную работу – записывают алгебраическое выражение (равенство, неравенство, формулу), выполняют указанное построение. При этом требуется не только воспроизвести заученную формулировку, а творчески подойти к заданию. Диктанты способствуют и развитию навыков логического мышления, и выработке умения работать с чертежными инструментами.
Известная не шаблонность постановки задачи и ограниченность времени на выполнение задания дисциплинируют учащихся, приучают к собранности, сосредоточенности, целеустремленности.
Проведение математических диктантов способствует и повышению общей грамотности учащихся. Опыт показывает, что в результате систематического использования этой формы работы резко уменьшается количество ошибок в написании математических терминов.
Цели опыта:
-повышение качества знаний учащихся по математике;
-развитие у учащихся способностей воспринимать информацию на слух;
-применение знаний в нестандартных ситуациях;
-воспитание ситуации успеха;
-формировать познавательный интерес к окружающему миру, желание развиваться;
- развивать умения слушать лекцию, речь учителя, товарищей, слушать вообще.
Задачи опыта:
-повышение мотивации учащихся к изучению предмета «Математика»;
-создание условий для творчества учителя и ученика;
-формирование активной позиции ученика на уроке и проявление его творческой индивидуальности;
-создание условий для формирования навыков самоорганизации и самообразования учащихся;
-раскрытие творческого потенциала учащихся, направленного на осознанный выбор профессии, связанной с математикой.
- вовлечь учащихся в познавательный процесс и позволить им осмысленно усваивать учебный материал.
- дать рекомендации по использованию математических диктантов на уроках математики.
Планируемый результат: научить учащегося не просто слушать, а слышать, что говорит учитель. Эффективно тренировать устойчивость внимания детей, оперативную память, умение сосредотачиваться.
Ведущая идея моего опыта предполагает использование математических диктантов с целью создания на уроках математики условий для личного развития учащихся, развития их индивидуальности. Создание педагогических ситуаций общения на уроке позволяет каждому ученику проявить самостоятельность, выборность в способах работы, творчество.
Дидактические функции математических диктантов ориентированы на систему упражнений, в которой ведущими являются приемы структурного анализа и синтеза, обобщения и конкретизации, классификации, аналогии, построения умозаключений, то есть на изучение способов и приемов, которые дают возможность подготовить учеников к более высокому уровню творческой деятельности, к решению более сложных «нестандартных» задач.
Свою задачу как педагога я вижу в том, чтобы сотрудничать с учащимися, воспитывать у них желание к поиску новых знаний, хочу, чтобы учащиеся умели выражать мысли, не используя «штампы» учебника, свободно владели математической терминологией, умели слушать и понимать сказанное учителем.
Я считаю, что математические диктанты наряду с устным опросом, самостоятельными и контрольными работами являются одним из эффективных способов осуществления связи между учителем и учащимися. Проведение математических диктантов способствует развитию логического мышления, повышению их математической культуры, обогащению математической речи. Выполняя задания диктанта, ученики приучаются к организованности, учатся экономить время, формируют привычку быстро сосредотачиваться. При помощи математических диктантов можно проконтролировать не только усвоение учениками изучаемой темы, но и проверить усвоение и закрепление только что поданного материала, диктанты помогут учителю выяснить, овладели ли учащиеся соответствующими умениями и навыками.
Итак, математическим диктантам необходимо отвести надлежащую роль в системе упражнений для усвоения базовых задач. Следует лишь применять их разумно, творчески, учитывая индивидуальные особенности учителя и учеников.
Сущность педагогического опыта
Успешное усвоение знаний, умений и навыков по предмету в целом можно обеспечить, если изучение материала учащимся будет осмысленным, а для этого они должны уметь не просто делать вид, что слушают учителя, а действительно его слушать и слышать то, о чём он говорит. В связи с этим в своей педагогической практике на уроках математики я и использую математические диктанты.
В диктантах можно выделить следующие группы заданий:
- операционные, в которых нужно вычислять, решать задачи, выполнять преобразования и т.п., получив информацию на слух;
- логические, в которых требуется оценить истинность высказывания, для чего необходимо быть внимательным и сосредоточенным, уметь слушать, слышать и анализировать данные;
- направленные на усвоение математической терминологии.
Предложенные задания обеспечивают содержательным учебным материалом этап устной работы в начале урока математики, а также этап подведения итогов в конце урока. Развитию грамотной математической речи способствует наличие в каждом диктанте образцов чтения математических выражений.
Важно подчеркнуть, что в силу специфики математических диктантов (воспринимаемые на слух вопросы; лаконичные ответы) их педагогические возможности ограничены. С их помощью, как правило, можно проверить, усвоили ли учащиеся обязательный минимум знаний, но нельзя организовать углубленную проверку. Поэтому ошибкой было бы противопоставлять диктанты другим формам контроля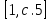 .
.
На уроках в 5 классе я использую графические диктанты. В тексте диктанта обычно приводится 10 решенных заданий, задания записаны на доске. Текст читает учитель. Темп чтения должен быть примерно таким, чтобы средний ученик успевал выполнить задание устно. Учащиеся в тетрадях записывают ответы к примерам при помощи значков _ - «верно», ^- «неверно». Сразу после выполнения диктанта, учитель показывает детям ключ к диктанту и выставляет оценки. Количество правильных ответов соответствует оценке, которую заработал учащийся за выполнение диктанта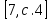 .
.
Например, графический диктант в 5 классе по теме «Повторение курса математики 1-4 класс» выглядит так:
Д-1
8
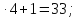
2+6
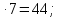
(2+6)
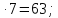
805:5=161;
2156:7=38;
9
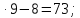
72:9+18-7=19;
60-38+5
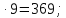
(74+7):(30-21)=9;
10) (36+6)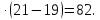
Ключ: _ _ ^ _^_^ ^ _^
Большой интерес для учащихся представляют цифровые диктанты. Суть цифрового диктанта в том, что учитель читает текст только один раз. Каждое предложение в диктанте несёт свою смысловую информацию – это может быть правило, аксиома, теорема, формула и т.д. Высказывание учителя может быть как истинным, так и, заведомо, ложным. Если ученик согласен с произнесённым высказыванием, то он ставит -1, а если нет, то -0. В диктанте приводится, обычно, 7 -8 высказываний. Я, обязательно, провожу математический диктант на том уроке, когда по плану проводится и самостоятельная работа (см. Приложение 3). Учащиеся это знают, готовятся к уроку, повторяют теоретический материал: формулы, определения, формулировки теорем. К проведению самостоятельной работы они уже подходят подготовленными теоретически, что положительно сказывается на отметке за письменную работу и способствует повышению качества знаний.
Вот пример диктанта, проводимого в 5 классе:
Натуральные числа
1.Натуральные числа используют для счёта предметов.
2. Самое первое натуральное число – это нуль.
2. Самое маленькое натуральное число – это 1.
4. Самое большое натуральное число – это десять миллионов.
5. Нельзя назвать самое большое натуральное число.
6. Для каждого натурального числа существует следующее за ним.
7. Два соседние натуральные числа отличаются на единицу.
Ответ: 1.010. 111.
Я применяю цифровые диктанты не только в 5-9 классах, но и в 10-11. Я считаю, что они дисциплинируют учащихся, заставляют старшеклассников систематически повторять формулировки правил и теорем. Начинать применение цифровых диктантов необходимо с первых уроков. Вот как может выглядеть диктант для 10 класса по теме “Аксиомы стереометрии”:
Аксиомы стереометрии
1. Прямые обозначаются одной маленькой буквой латинского алфавита.
2. В пространстве на любой плоскости выполняются все аксиомы и теоремы планиметрии.
3. Основные фигуры в пространстве – это прямые и плоскости.
4.Через любые три точки пространства проходит только одна плоскость.
5. Если две плоскости имеют общую точку, то больше общих точек у них нет .
6. Если два пункта прямой лежат в плоскости , то и вся прямая находится в этой плоскости.
7. Любую аксиому можно доказать.
Ответ: 1.100.010.
Тексты конкретных цифровых диктантов приведены в Приложении 1.
Тексты к цифровым диктантам я составляю сама. Я разрабатываю перечень вопросов по определённой теме курса алгебры или геометрии. На эти вопросы нужно чётко отвечать “да” или “нет”. Потом, в зависимости от цели урока, составляю подборку к конкретному цифровому диктанту (см. Приложение 2).
В течение 2014/2015 учебного года в 8 классе я систематически применяла цифровые диктанты на уроках. В результате, к окончанию учебного года, средний балл за четверть увеличился на 0,6 (см. Приложение 4). Поэтому я считаю, что имеет смысл, наряду с другими формами контроля, применять и математические диктанты.
Конечно, применение диктантов может вызывать определённые трудности:
Много времени тратится на подготовительную работу.
Проведение диктанта требует от учителя весьма большого напряжения: надо читать в оптимальном темпе тексты заданий, следить за классом, реагировать на практически неизбежные сбои.
Если требуются иллюстрации к вопросам, то к уроку нужно готовить дополнительный материал.
Этих трудностей можно избежать, если воспользоваться готовыми математическими диктантами, которые легко найти в интернете.
Созданы уникальные сборники математических диктантов для 5-6 классов и 10-11 классов со звуковым сопровождением и иллюстрацией каждого вопроса. Математический диктант записан в формате, который можно запустить на стандартном проигрывателе Windows, можно вставить в презентацию PowerPoint.
Как организовать проведение математического диктанта.
Для диктантов лучше использовать листы бумаги (бланки ответов, см. Приложение 5). Можно использовать при проведении диктанта два бланка ответов для того, чтобы ученик мог один бланк сдать учителю, а второй использовать для проверки правильности выполнения работы. Если есть закрытые доски, то можно, либо написать ответы заранее, либо вызвать два ученика к доске и их ответы проверить вместе с классом. Опять же можно использовать презентацию. Проверка сразу на уроке даёт возможность ещё раз закрепить изученный материал. Кроме того, выполнив любой вид работы, каждый ребёнок жаждет быстрее узнать результаты своей работы и оценку за неё. Вспомните: после контрольных, самостоятельных работ сколько раз мы слышали эту фразу: «Я уже сдал тетрадь, а покажите, какой там ответ или как это решается?» Если диктант проводится сразу после изучения нового материала, то можно проверить ответы, обсудить результаты.
В заключение хочу сказать, что учащимся сложно воспринимать информацию на слух. Что верно, то верно: учащимся, не привыкшим к математическим диктантам, воспринимать задания на слух действительно трудно. Но если диктанты проводятся часто и систематически, то школьники приучаются выполнять задания на слух, а ценность такого умения неоспорима.
ЛИТЕРАТУРА:
В.И. Жохов Математические диктанты в 6 классе // Мнемозина – 2014, с.5-12
Е.П. Кузнецова Математика: учебное пособие для 5 класса учреждений общего среднего образования с русским языком обучения: в 2 ч. // - Минск: Национальный институт образования– 2013. –Ч.1
Е.П. Кузнецова Математика: учебное пособие для 5 класса учреждений общего среднего образования с русским языком обучения : в 2 ч. // - Минск : Национальный институт образования– 2013. –Ч.2
Е.П. Кузнецова Алгебра: учебное пособие для 9 класса учреждений общего среднего образования с русским языком обучения // - Минск: Народная асвета – 2014
Л.В. Макарова Уроки-практикумы в системе работы учителя // Математика в школе – 1998 №3, с.13-15
П.Б. Ройтман Повышение вычислительной культуры учащихся // Пособие для учителя – 1988, с.8-14
В.В. Тарасова Графические диктанты // Математика Первое сентября– 2001 №47, с.4-7
В.В. Шлыков Геометрия: учеб. пособие для 10 класса учреждений общего среднего образования с русским языком обучения //Минск: Народная асвета – 2013
Приложение 1
Сравнение натуральных чисел, 5 класс
1. Сравнить два числа- это, значит, определить которое из них больше, а которое меньше.
2. Меньшее число расположено правее на координатном луче, а большее -левее.
3. Самое маленькое натуральное число – это 0.
4. Из двух натуральных чисел меньше то, у которого меньше разрядов.
5. Ноль больше за единицу.
6. Никто не знает самое большое натуральное число.
7. Два натуральные числа с одинаковым количеством разрядов сравнивают поразрядно.
Ответ 1.001.011.
Решение уравнений, 5 класс
1. Уравнение- это равенство, которое содержит букву, значение которой надо найти.
2. Чтобы найти неизвестное слагаемое надо к сумме прибавить известное.
3. У уравнения может быть корень, а может его и не быть.
4. 100 :4 =20.
5. Икс –это буква из белорусского алфавита.
6. При вычитании числа называют: множитель, множитель, произведение.
7. Уравнение 5х=0 не имеет решения.
Ответ: 101.000.0.
Плоские и пространственные фигуры, 7 класс
Слово “геометрия” в переводе с греческого означает “плоскость”.
Геометрия состоит из двух частей : планиметрия и алгебра.
Геометрические фигуры – это треугольник, квадрат, куб, шар.
Прямоугольный параллелепипед состоит из 6 кругов.
Куб можно назвать многогранником.
Большое влияние на развитие геометрии оказали древнегреческие учёные.
Точка не имеет размеров.
У прямой можно определить длину и ширину.
Ответ: 00.101.110.
Теорема Пифагора, 8 класс
1. Стороны прямоугольного треугольника называются : катет, гипотенуза и гипотенуза.
2. Пифагор – это великий белорусский учёный.
3. Треугольник со сторонами 3,4,5 называется персидским.
4. Катет, который лежит против угла 30 ,равен половине гипотенузы.
,равен половине гипотенузы.
5. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
6. Гипотенуза короче чем катет.
7. Существует только одно доказательство теоремы Пифагора.
8. Треугольник со сторонами 6,8,10 является прямоуголным.
Ответ: 00.011.001.
Площадь параллелограмма и треугольника, 8 класс
1. Площадь треугольника равна призведению его смежных сторон.
2. Площадь квадрата со стороной 5см равна 20см.
3. Чтобы найти площадь параллелограмма, надо сторону поделить на высоту, проведённую к этой стороне.
4. Площадь треугольника равна половине произведения длины стороны на высоту, прведённую к этой стороне
5. Площадь измеряется в мм, см и м.
6. В прямоугольном треугольнике катет является высотой.
7. Чтобы найти площадь прямоуголного треугольника необходимо катет умножить на катет.
8. Площадь прямоугольного треугольника с катетами 8см і 2см равна 8см .
.
Ответ: 00.010.101.
Основные понятия, 10 класс
Планиметрия – это геометрия на плоскости.
К пространственным фигурам относятся: пирамида, куб, шар, цилиндр.
Основными понятиями стереометрии являются: точка, плоскость, кривая.
За изображение параллельных прямых принимают пересекающиеся прямые.
Многогранник состоит из многоугольников, которые называют гранями.
Параллелепипед – это многогранник, у которого 8 граней.
Прямой параллелепипед – это такой параллелепипед, у которого боковые грани прямоугольники.
Ответ : 1.100.101
Аксиомы стереометрии, 10 класс
Аксиома – это утверждение, которое необходимо доказать.
Основные фигуры стереометрии –это пункт, прямая, плоскость.
Плоскости обозначаются маленькими буквами латинского алфавита.
Существует пять аксиом, которые выражают основные свойства взаимного расположения пунктов, прямых и плоскостей.
Через любые три точки не лежащие на одной прямой, проходит единственая плоскость.
Если один пункт прямой лежит в плоскости, то и вся прямая лежит в этой плоскости.
Если две плоскости имеют общую точку, то они пересекаются по прямой.
Ответ: 0.100.101
Следствия из аксиом, 10 класс
1.Плоскость в пространстве можно задать при помощи трех точек, которые не лежат на одной прямой.
2. Если точка не лежит на прямой, то эта точка и прямая задают плоскость.
3. Теорема – это утверждение, которое не требует доказательства.
4.Если две плоскости имеют общую точку, то все остальные точки тоже лежат на этой прямой.
5.Через две пересекающиеся прямые нельзя провести плоскость.
6.Три точки всегда лежат в одной плоскости.
7. Аксиома – это маленькая теорема.
Ответ: 1.101.010.
Приложение 2
Перечень вопросов, которые можно использовать для составления цифрового диктанта по теме “Площадь”:
ТЕМА: Площадь.
Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
За единицу измерения площадей принимают только квадрат со стороной 1 см.
Площадь многоугольника выражается только положительной величиной.
Верно ли, что равные многоугольники имеют равные площади?
Если многоугольник разбит на части, то его площадь равна сумме площадей этих частей.
Площадь квадрата равна кубу его стороны.
Площадь прямоугольника равна половине произведения его противоположных сторон.
Площадь прямоугольника равна произведению его соседних сторон.
Основание – это одна из сторон параллелограмма.
Высота треугольника – это перпендикуляр, опущенный из любой точки противоположной стороны к прямой, содержащей основание.
Площадь параллелограмма равна половине произведения высоты на основание.
Одну из сторон треугольника называют основанием.
Площадь треугольника равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника равна произведению его катетов.
Если основания двух треугольников равны, то их площади относятся как высоты.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Высота трапеции – это перпендикуляр, проведенный к боковой стороне.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Площадь ромба равна произведению его диагоналей.
Площадь ромба можно найти по той же формуле, что и параллелограмм.
Теорема Пифагора используется в любых треугольниках.
В прямоугольном треугольнике квадрат любого катета равен сумме квадратов гипотенузы и другого катета.
Пифагоровы треугольники те, у которых длины сторон выражаются целыми числами.
Треугольник со сторонами 3, 4, 5 называют египетским треугольником.
КЛЮЧ:
«1» - 1; 3; 4; 5; 8; 9; 10; 12; 13; 16; 18; 20; 23; 24
«0» - 2; 6; 7; 11; 14; 15; 17; 19; 21; 22;
Разложение квадратного трёхчлена на линейные множители
Цели:
Формировать представление о квадратном трёхчлене и его разложении на линейные множители;
Организовать деятельность, направленную на практическое применение теоремы о разложении квадратного трёхчлена на линейные множители;
Создать условия для развития познавательных умений – применить знания, сделать вывод, работать с учебником;
Способствовать воспитанию устойчивого интереса к предмету, положительного отношения к учению.
Форма урока: лекционно-практическая
Подготовительный этап: запись на доске даты, темы, устных упражнений, таблица настроения.
Ход урока
1. Проверка домашнего задания - устно;
2. Считаем устно;
3. Ответ на вопрос: что необходимо на уроке?
4. Математический диктант;
5. Самостоятельная работа;
6. Физкультминутка ;
7. Объяснение нового материала;
8. Практическое применение полученных знаний;
9. Подведение итогов урока, рефлексия.
1. Проверка домашнего задания – устно.
2. Считаем устно: назвать коэфициенты квадратного уравнения
1)5х2 +2х -4 =0; 2)-х+9х2 =0; 3)7х2 -4=0; 4) 8х2 =3х+2; 5) 0=9х2 =3х-2.
3. Ответ на вопрос: что необходимо на уроке?
Решите устно примеры и скажите, что на сегодняшнем уроке вам необходимо?
1.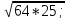 в) 40; т) 0,4.
в) 40; т) 0,4.
2. х2 =25; р) 5; н) 5;-5;
3. 7х2 =0; и) 0; о) -7;
4. 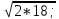 м) 6; е) -6;
м) 6; е) -6;
5. 4х2 =16. н) 4; -4; а)2; -2.
6. х2 =625 и) 25;-25; р) 15; -15;
7. 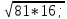 а) 18; е) 36.
а) 18; е) 36.
Ответ: внимание.
4. Математический диктант:
Ответы на вопросы диктанта проверяются сразу после его написания и обсуждаются всем классом.
1. Уравнение ах+в =0 называется квадратным.
2. Если D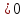 , то уравнение имеет 2 корня.
, то уравнение имеет 2 корня.
3. Дискриминант позволяет определить количество корней квадратного уравнения.
4. ах2 =0- неполное квадратное уравнение.
5. Если х2 =25, то х=5-единственное решение уравнения.
6. Квадратное уравнение является уравнением второй степени с одним неизвестным.
7. Старший коэффициент уравнения х2 +3х +4 =0 равен 0.
Ответ: 011.101.0
5. Самостоятельная работа
1.Решить уравнение: а) х2 =16; б) х2 -25=0.
2. Указать количество корней уравнения: х2 +х-3=0.
3. Решить уравнение: а) 2 х2 +3х – 5=0; б) 8 х2+2х-3=0.
4. Разложить число 58 на два множителя так ,чтобы их сумма была равна 31.
5. Решить уравнение : х2+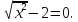
6. Физкультминутка:
Уравнение является : а) квадратным; б) линейным.
3х-5=0; 2х=3 ; х+1=0; 13 х2-11х=0; 1- х2 =0; 2 х2 =11; 5х-11=0; 6 х2-х4 +9=0; х3 +5х-17=0.
если “да”-руки вытянуть вперед;
если “нет” – хлопок в ладоши над головой.
7. Объяснение нового материала:
1. Дать определение квадратного трёхчлена, дискриминанта квадратного трёхчлена, корня квадратного трёхчлена.
2. Рассмотреть теорему о разложении квадратного трехчлена на линейные множитнли.
3. Разобрать решение примеров 1,2 из учебника.
8. Практическое применение полученных знаний
Решение на доске № 5.72, 5.73( нечётные)
9. Подведение итогов урока,рефлексия.
Таблица настроения
10. Домашнее задание № 5.72(2,4,6,8)
Приложение 4
Приложение 5
Бланк ответов.
Ф.И. ученика _______________________________
Класс__________ Дата_____________
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ
|
|
|
|
|
|
|
|
|
|
|
18

 Получите свидетельство
Получите свидетельство Вход
Вход












 Математические диктанты и их роль в учебном процессе (131.1 KB)
Математические диктанты и их роль в учебном процессе (131.1 KB)
 0
0 2910
2910 41
41 Нравится
0
Нравится
0


