Машина Поста (устройство, команды и принцип работы)

Машина Поста

Практически одновременно с Тьюрингом (тоже в 1936 году) и независимо от него, американский математик Эмиль Пост предлагает еще более простого исполнителя, названного позже машиной Поста. Обе машины «эквивалентны» и были созданы для уточнения понятия «алгоритм». 

Эмиль Леон  Пост - американский математик и логик.  Один из основателей многозначной логики (1921);  трудился в области математической логики: создал алгебру Поста, классы Поста функций алгебры логики; предложил абстрактную вычислительную машину — машину Поста.

Машина Поста – это абстрактная (несуществующая реально) вычислительная машина, созданная для уточнения (формализации) понятия алгоритма. Представляет собой универсальный исполнитель, позволяющий вводить начальные данные и читать результат выполнения программы.

В 1936 г. американский математик Эмиль Пост в статье описал систему, обладающую алгоритмической простотой и способную определять, является ли та или иная задача алгоритмически разрешимой. Если задача имеет алгоритмическое решение, то она представима в форме команд для машины Поста.

Структура машины Поста:

Машина Поста состоит из каретки (или считывающей и записывающей головки) и разбитой на ячейки бесконечной в обе стороны ленты (также как у машины Тьюринга). Каждая ячейка ленты может быть либо пустой — 0, либо помеченной меткой 1. За один шаг каретка может сдвинуться на одну позицию влево или вправо, считать, поставить или стереть символ в том месте, где она стоит. 

Т.о., Пост сократил алфавит всего до двух цифр. Это допустимо, потому что любые данные можно перекодировать в двоичный код, сопоставив каждой букве исходного алфавита уникальную последовательность нулей и единиц.

Алгоритм работы машины Поста задается не в виде таблицы, а как программа для универсального исполнителя. 

Программа  состоит из конечного числа строк и использует всего 6 команд.

N. → J  - сдвиг вправо

N. ← J - сдвиг влево

N. 1 J - запись метки

N. 0 J  -удаление метки

N. ? J1, J0 - если в ячейке есть метка, то перейти к j1 строке программы, иначе перейти к j0 строке программы.

N. Stop - остановка

где N. — номер строки, J — строка на которую переходит управление далее.

Попытка стереть метку там, где ее нет, или поставить метку повторно считается ошибкой, и машина аварийно останавливается.

Для работы машины нужно задать программу и ее начальное состояние (т. е. состояние ленты и позицию каретки).

После запуска возможны варианты:

- работа может закончиться невыполнимой командой (стирание несуществующей метки или запись в помеченное поле);

- работа может закончиться командой Stop;

- работа никогда не закончится.

Все строки в программе нумеруются по порядку, это необходимо для работы команды ветвления (? n0,n1). С помощью этой команды можно также строить циклы, как с предусловием, так и с постусловием.

Пост предположил, что любой алгоритм может быть записан как программа для машины Поста.
В теории алгоритмов доказано, что машины Поста и Тьюринга одинаковы по своим возможностям. Это значит, что круг задач, который они решают, тоже одинаков.

Например, следующая программа перемещает каретку влево до первой отмеченной ячейки:
1. ←
2. ? 1,3
3. стоп

После команд "←”, "→”, "0” и "1” можно указать номер строки, на которую нужно перейти сразу после выполнения этой команды. Например, команда ← 3 означает "переместить каретку влево и перейти на строку 3”.

При работе с машиной Поста числа обычно записывают в унарной (единичной) системе счисления, в виде непрерывной цепочки меток нужной длины (вспомните счетные палочки в младшей школе).

Задачи:

1. Напишите программу для машины Поста, которая увеличивает (уменьшает) число в единичной системе счисления на единицу. Каретка расположена слева от числа.

2. Напишите программу для машины Поста, которая складывает два числа в единичной системе счисления. Каретка расположена над пробелом, разделяющим эти числа на ленте.

3. Что делают следующие программы для машины Поста:
а) 1  1                 б) 1   ←                           в)  1      ? 2,3
    2  →                    2   ? 3,4                            2      1 4
    3  → 1                 3   1 1                               3      → 1
                              4   стоп                            4      стоп

Пример работы машины Поста:

Задача: увеличить число 3 на единицу (изменить значение в памяти с 3 на 4).

Целое положительное число на ленте машины Поста представимо идущими подряд метками, которых на одну больше, чем кодируемое число. Это связано с тем, что одна метка обозначает ноль, а уже две – единицу, и т.д.

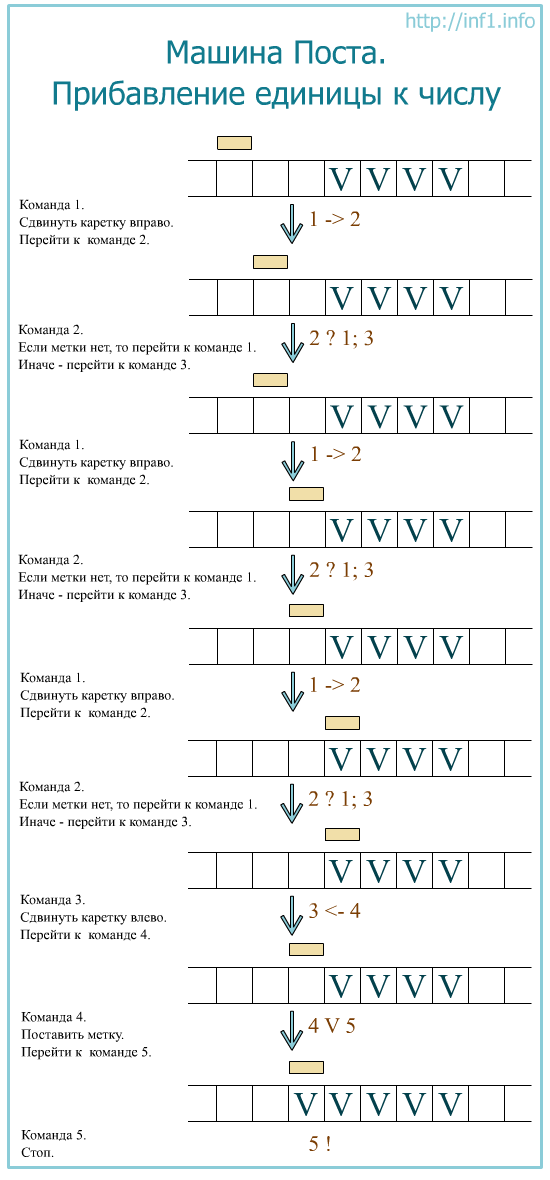
Допустим, точно известно, что каретка стоит где-то слева от меток и обозревает пустую ячейку. Тогда программа увеличения числа на единицу может выглядеть так:

1 → 2
2 ? 1;3
3 ← 4
4 V 5
5 Stop
А процесс выполнения может быть таким (см.рисунок):