Измерение отрезков

Цели урока:
1) Обучающая: формирование знаний о длине отрезка, свойствах длин отрезка, инструментах измерения отрезков; формирование умений измерять данный отрезок и выразить его длину в миллиметрах, сантиметрах, метрах
2) Развивающая: развитие умений применять полученные теоретические знания на практике, развитие внимания, аналитических способностей.
3) Воспитывающая: воспитание интереса к изучению математики, ответственности, самостоятельности.
Литература: «Геометрия 7 — 9 класс» Л. С. Атанасян и др.
План урока:
1. Организационный момент.
2. Актуализация опорных знаний.
3. Получение знаний.
4. Закрепление нового материала.
5. Рефлексия.
6. Домашнее задание.
Ход урока:
1. Организационный момент.
Приветствие учащихся. Ставятся цели и определяются задачи урока.
Объявляется тема урока. Учащиеся записывают тему урока и дату в рабочих тетрадях.
2. Актуализация опорных знаний.
На прошлом уроке мы говорили о сравнении двух отрезков способом наложения их друг на друга.
— Скажите, в каком случае два отрезка называют равными? (если их можно совместить наложением)
Сегодня на уроке мы снова поговорим об измерении отрезков, а точнее научимся измерять отрезки и выражать их длину в миллиметрах, сантиметрах, метрах.
Для начала, давайте, ответим на несколько вопросов.
— Что называют серединой отрезка?
— Что называют биссектрисой угла?
3. Получение знаний.
В повседневной жизни нам часто приходится сталкиваться с измерением высот зданий, сооружений, а также с измерением расстояний, которые мы прошли или проехали. С точки зрения геометрии мы имеем в таких случаях дело с измерением отрезков.
Измерение отрезков основано на сравнении их с некоторым отрезком, принятым за единицу измерения. Такой отрезок также называют масштабным отрезком.
Давайте определим длину некоторого отрезка АВ, приняв за единицу измерения сантиметр (рисунок 1). Видим, что в данном отрезке АВ сантиметр укладывается ровно четыре раза, а это означает, что его длина равна четыре сантиметра. Обычно говорят кратко: «Отрезок АВ равен четыре сантиметра». А записывают так: АВ = 4 см.
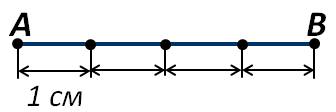
Рисунок 1.
Но может оказаться так, что отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке.
Возьмём отрезок CD (рисунок 2). Сантиметр укладывается в отрезок пять раз, но при этом получается остаток. В таком случае единицу измерения необходимо разделить на равные части, обычно делят на десять равных частей, и определить, сколько таких частей укладывается в остатке. В нашем случае в остатке шесть раз укладывается десятая часть отрезка, поэтому длина отрезка CD равна пять целых шесть десятых сантиметра. Отметим, что одну десятую часть сантиметра называют миллиметром (мм).
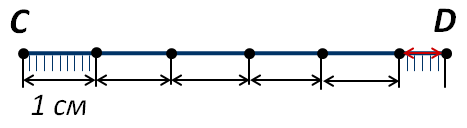
Рисунок 2.
Однако может возникнуть ситуация, когда и миллиметр не будет укладываться в остатке целое число раз, и получится новый остаток. Тогда и миллиметр можно разделить на 10 частей и продолжить процесс измерения.
Единицей измерения отрезка может быть не только сантиметр, но и другой отрезок.
Выбрав единицу измерения, можно измерить любой отрезок,
Исходя из проделанного выше, можно сказать, что это число показывает, сколько раз единица измерения и её части укладываются в измеряемом отрезке.
Возьмём два равных отрезка АВ и СD (рисунок 3). Единицы измерения в этих отрезках укладываются одинаковое число раз,
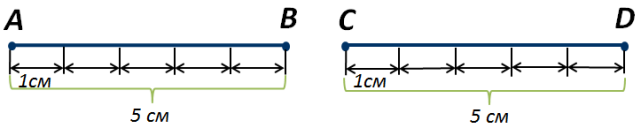
Рисунок 3.
Если же мы возьмём два неравных отрезка KL и MN (рисунок 4), то увидим, что в меньшем отрезке MN единица измерения укладывается меньшее число раз, чем в отрезке KL,
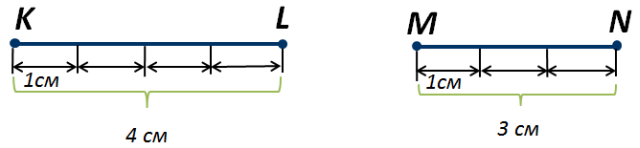
Рисунок 4.
Теперь рассмотрим отрезок АВ (рисунок 5). Точка С делит его на два отрезка: АС и СВ. Измерим эти отрезки. Видим, что отрезок АС равен четыре сантиметра, отрезок СВ равен три целых пять десятых сантиметра и отрезок АВ равен семь целых пять десятых сантиметра. Получили:
АС + СВ = АВ.
Таким образом, сформулируем следующее.
Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
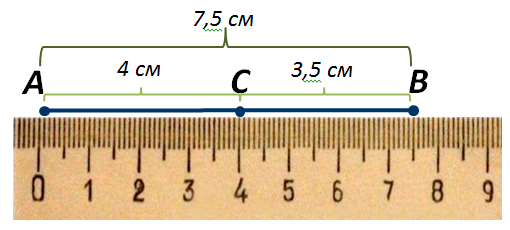
Рисунок 5.
Следует сказать, что если длина некоторого отрезка АВ в k раз больше отрезка CD, то записывают это следующим образом: АВ=kCD.
Отметим также, что длина отрезка называется расстоянием между концами этого отрезка.
Поговорим о единицах измерения. Для измерения отрезков и нахождения расстояний используются различные единицы измерения. Стандартной международной единицей измерения отрезков является метр — отрезок, который приблизительно равен 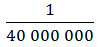 земного меридиана. Эталон метра хранится в Международном бюро мер и весов во Франции.
земного меридиана. Эталон метра хранится в Международном бюро мер и весов во Франции.
В одном метре сто сантиметров (1 м =100 см), а один сантиметр содержит десять миллиметров (1 см = 10 мм).
При измерении небольших расстояний, например, расстояния между точками на листе бумаги или нахождении длины карандаша за единицу измерения принимают сантиметр или миллиметр. Высоту дерева можно измерить в метрах. А вот расстояние, которое мы пройдём на лыжах, можно измерить в километрах.
Можно также использовать и такие единицы измерения, как дециметр (1 дм = 10 см), морская миля, равная одной целой восьмистам пятидесяти двум тысячным километра (1 миля = 1,852 км). А вот для измерения очень больших расстояний в астрономии используется такая единица измерения, как световой год (это путь, который проходит свет в течение одного года).
Для измерения расстояний могут использоваться различные инструменты. Например, в техническом черчении используется масштабная миллиметровая линейка. Для измерения расстояний на местности пользуются рулеткой. А вот для измерения диаметра трубки можно воспользоваться штангенциркулем.
4. Закрепление нового материала.
Для закрепления материала учащимся предлагается выполнить следующие практические задания.
Задание 1. На прямой отмечены точки А, В и С. Отрезок АВ = 50 мм, а отрезок АС = 1,7 дм. Найдите длину отрезка ВС в сантиметрах. Рассмотрите различные варианты взаимного расположения точек.
Решение: Переведём значения длин отрезков в сантиметры.
АВ = 50 мм = 5 см; АС=1,7 дм =17 см.
1)

Рисунок 6.
ВС = АС — АВ, ВС = 17 см — 5 см = 12 см.
2)

Рисунок 7.
ВС = АВ + АС, ВС = 5 см + 17 см = 22 см.
3)

Рисунок 8.
В данном случае задача не имеет решения, так как АС > АВ.
Ответ: 12 см или 22 см.
Задание 2. На прямой MN лежит точка L. Найдите длину отрезка MN, если ML = 7 см, а LN = 4ML.
Решение: MN = ML + LN = ML + 4ML = 5ML;

Рисунок 9.
MN = 5*7 =35 см.
Ответ: 35 см.
Задание 3. Точка О — середина отрезка KL, длина которого равна 8,4 см. От точки О на прямой KL отложены отрезки ОМ = 2 см и ON = 5 см. Найдите длины отрезков КМ и KN, если MN = 3 см.

Рисунок 10.
Решение: Так как О — середина отрезка KL, то KO = ОL = 4,2 см.
KM = KO + OM = 4,2 + 2 =6,2 см.
KN = KL + LN.
Из последнего выражения видим, чтобы найти длину отрезка KN, нам необходимо найти длину отрезка LN.
Так как ОL = 4,2 см и ON = 5 см, то LN = ON — ОL = 5 — 4,2 = 0,8 см.
Тогда KN = 8,4 + 0,8 = 9,2 см.
Ответ: 6,2 см; 9,2 см.
5. Рефлексия.
Подводятся итоги урока, обсуждается, что учащиеся узнали. Учащиеся задают вопросы, возникшие при изучении нового материала и выполнении практических заданий. Затем ребята по кругу высказываются одним предложением, выбирая начало фразы записанной на доске:
1. сегодня я узнал…
2. было интересно…
3. было трудно…
4. я выполнял задания…
5. я понял, что…
6. я научился…
7. у меня получилось …
Оценивается работа учащихся на уроке.
6. Домашнее задание: § 4, № 26, 34.
Получите комплекты видеоуроков + онлайн версии
Похожие записи
 21054
21054 Нравится
0
Нравится
0
Комментарии 1
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
 Нравится
0
Нравится
0

 Получите свидетельство
Получите свидетельство Вход
Вход









