На прошлом уроке мы узнали:
· Для удобства хранения и передачи информации её часто переводят из непрерывной формы в дискретную. Такой процесс называется дискретизацией.
· В процессе дискретизации информация записывается на одном из языков.
· Алфавитом языка называются все существующие символы, которые используются для представления информации на этом языке.
· Алфавит характеризуется своей мощностью, это количество символов, которые в него входят.
· Двоичный алфавит состоит из двух символов. Запись информации с помощью такого алфавита называется двоичным кодированием.
· Двоичный код – это код информации, получившийся в результате её двоичного кодирования.
· Любой алфавит можно привести к двоичному.
Вопросы:
· Двоичное кодирование звука.
· Двоичное кодирование изображения.
· Равномерный и неравномерный коды.
· Двоичное кодирование текстовых сообщений методом Хаффмана.
Итак, на прошлом уроке мы узнали, что любой алфавит можно представить в виде двоичного, для этого каждому символу исходного алфавита присваивается его двоичный код. Записывая подряд двоичные коды всех символов, мы можем кодировать текстовые сообщения. Ещё мы узнали, что двоичный алфавит легко реализовать технически, с помощью наличия или отсутствия электрического сигнала на некотором участке электрической цепи. Именно поэтому любая информация на компьютере представлена в виде двоичного кода. Однако мы знаем, что на компьютере может храниться любая информация, а не только текстовая или числовая. Как же её представить в виде двоичного кода? Например звук и изображение. Как мы знаем, они представляются в виде непрерывных сигналов, разберёмся как же представить эти два вида информации в дискретной форме.
Начнём с изображения. Вполне логично, что любое изображение можно разделить на некоторые участки, каждый из которых имеет свой цвет. Именно так происходит при представлении изображений на компьютере. Изображение разбивается на маленькие фрагменты, которые можно назвать точками. Каждое изображение имеет своё разрешение. Оно состоит из двух цифр, которые разделяются крестиком или двоеточием. Число слева, означает, на сколько точек делится изображение по горизонтали, а справа – на сколько по вертикали. Таким образом изображение на компьютере представляется в виде последовательности точек, каждая из которых имеет свой цвет. То есть изображение на компьютере можно представить, последовательно записав цвета всех точек, которые в него входят.
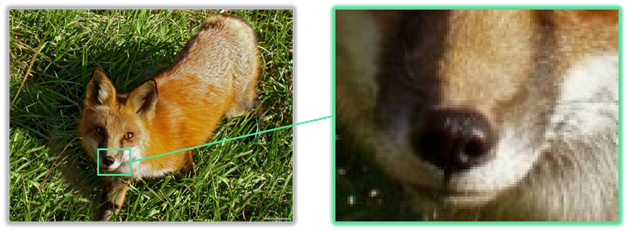
Но как же представить цвет в виде двоичных кодов? Любой цвет на мониторе компьютера изображается смешиванием в разных количествах трёх основных цветов: красного, зелёного и синего. Такое представление цветов называется их RGB-моделью. По первым буквам названий основных цветов на английском языке, то есть «Rad», «Green» и «Blue». Так, как остальные цвета – это смеси трёх основных цветов в разных количествах, их можно представить в виде трёх чисел, количеств основных цветов. Эти числа можно заменить двоичными кодами одинаковой разрядности. Записав эти коды последовательно, мы получим двоичный код цвета точки. Таким образом изображение на компьютере представляется в виде списка двоичных кодов одинаковой разрядности, каждый из которых обозначает цвет одной из точек изображения.
Немного иначе происходит двоичное кодирование звука. Позже из курса физики вы узнаете, что любой звук можно представить в виде непрерывной волны. Эту волну можно описать, зависимостью её амплитуды, то есть громкости звука от времени. Такую зависимость легко изобразить в виде графика. Чтобы представить звук в виде дискретных сигналов, время, в течение которого продолжается звук, делится на равные небольшие промежутки. И на каждом из промежутков заново определяется амплитуда волны, то есть громкость звука.
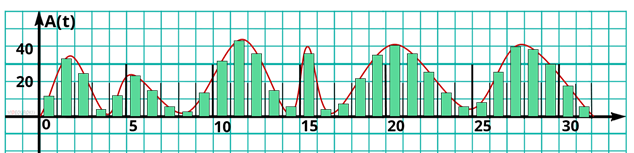
Дискретизация звука
То, есть звук можно представить в виде списка чисел, каждое из которых означает амплитуду волны, в течение небольшого промежутка времени. Эти числа можно представить в виде двоичных кодов с одинаковым количеством разрядов. Таким образом звук на компьютере представляется в виде списка двоичных кодов одинаковой разрядности, каждый из которых обозначает амплитуду звуковой волны на некотором небольшом промежутке времени.
Мы знаем, что с помощью двоичного кодирования в виде последовательности единиц и нулей можно представить любую информацию на естественном или формальном языке, в том числе изображение и звук. То есть информацию из любой формы можно представить в виде двоичного кода, что означает универсальность двоичного кодирования. Это и есть его главное преимущество. Главный недостаток двоичного кодирования – это большой размер двоичного кода. Так при кодировании текстового сообщения одному символу текста может соответствовать несколько символов двоичного кода.
Давайте подумаем, как можно уменьшить размер двоичного кода, и вообще любого кода. До этого все двоичные коды, которые мы рассматривали, были равномерными. Равномерным называется код, который состоит из равных по количеству разрядов кодовых комбинаций. Так например при кодировании алфавита для каждой буквы мы использовали двоичные коды с одинаковым количеством разрядов. Однако не все символы алфавита в текстовом сообщении, встречаются одинаково часто. Поэтому, для того, чтобы сократить длину двоичного кода мы можем присвоить разным сигналам коды разной длины. Коды с меньшей разрядностью можно присвоить сигналам, которые в сообщении встречаются чаще, а коды с большей разрядностью – сигналам, которые встречаются в сообщении реже. Такой код называется неравномерным, то есть он состоит из комбинаций различной длины.
Пример неравномерного кода – азбука Морзе. В ней разным буквам алфавита, соответствует разное количество сигналов, длинных и коротких. Например буква «А» обозначается всего двумя сигналами: одним коротким и одним длинным. А твёрдый знак кодируется пятью сигналами: двумя длинными, одним коротким и двумя длинными.
Рассмотрим один из методов неравномерного кодирования текстовых сообщений. Он называется методом Хаффмана. Посмотрим, как работает этот метод, закодировав с его помощью сообщение: «МАМА МЫЛА РАМУ». Сначала выпишем все символы алфавита, который используется в сообщении. В данном сообщении используются символы: «М», «А», пробел, «Ы», «Л», «Р» и «У». Затем нужно записать, как часто в сообщении встречается каждый из символов. Буквы «М» и «А» повторяются по четыре раза. Пробел повторяется дважды. Буквы «Ы», «Л», «Р» и «У» в сообщении встречаются по одному разу. Затем символы сообщения записываются в порядке убывания частоты появления. У нас они так и записаны.
Теперь строится дерево частоты появления символов в сообщении. В начале берутся два символа, которые встречаются в сообщении реже всех. У нас таких символа четыре, возьмём два правых, буквы «Р» и «У», соединяем их линией, и складываем их частоту появления в сообщении. 1 + 1 = 2.

Теперь повторим то же действие. Реже всех у нас появлялись буквы «Ы» и «Л». Соединим их линиями сложив частоту появления получим 2.
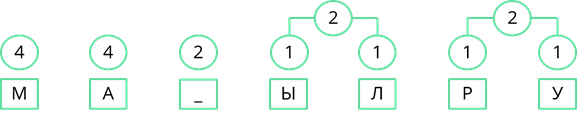
Теперь снова смотрим где у нас самая маленькая частота появления. Таких частот у нас три. Пробел появлялся дважды, двум равны и общие частоты появления символов «Ы» и «Л», и символов «Р» и «У». Возьмём две правые частоты и объединим их. Их суммарная частота равна 4.
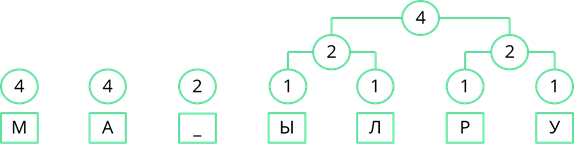
Снова ищем минимальные частоты появления. Возьмём две правые частоты и объединим их. Их сумма равна 6.
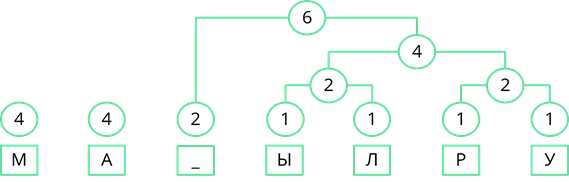
Теперь объединим две левые частоты. Их сумма равна 8.
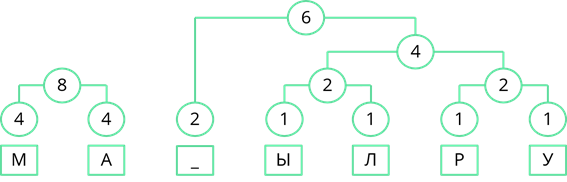
Объединим две оставшиеся частоты. Их сумма равна 14. Именно четырнадцати равна длина кодируемого сообщения.
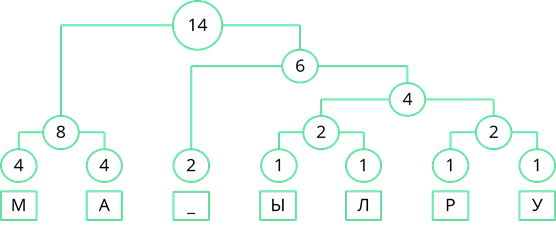
Теперь двигаясь, сверху вниз присвоим ветвям дерева значения 0 и 1. Ветви, с большей частотой будем присваивать 1, а ветви с меньшей частотой – 0. Так левой ветви верхнего узла присвоим 1, а правой – 0.
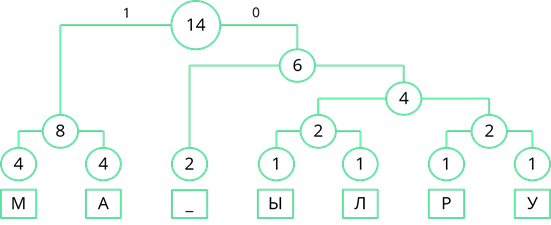
Затем рассмотрим левый узел. Там две частоты равны. Поэтому левой ветви присвоим 0, а правой – 1.
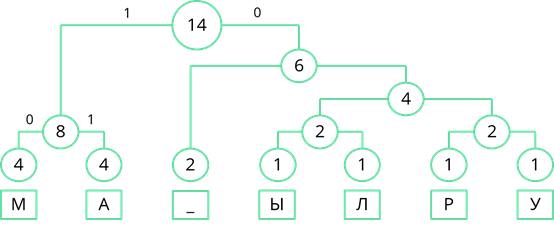
Рассмотрим узел, частота которого равна 6. Частота появления пробела меньше суммарной частоты правой ветви. Поэтому левой ветви присвоим 0, а правой ветви – 1.
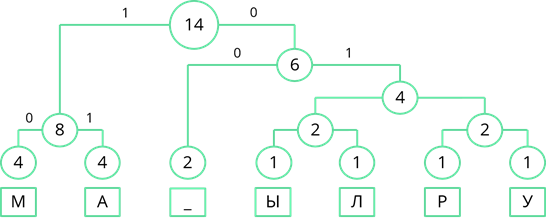
По такому же принципу пронумеруем оставшиеся ветви дерева.
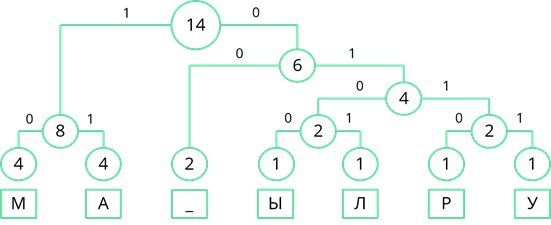
Теперь, двигаясь по получившемуся дереву сверху вниз, мы можем записать двоичный код каждого символа. Так у буквы «М» будет код 10, у буквы «А» – 11, у пробела – 00 и т. д…
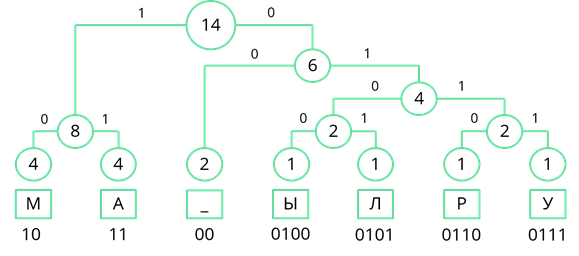
Теперь нам остаётся лишь заменить все символы в сообщении их двоичными кодами. В итоге двоичный код нашего сообщения будет 101110110010010001011100011011100111. Всего в нём 36 разрядов.
У некоторых из вас может возникнуть вопрос, а как же расшифровать такое сообщение, ведь в отличии от равномерного кода мы не знаем точно сколько разрядов занимает каждый символ. При неравномерном кодировании достаточно, чтобы код никакого из символов не начинался с кода другого символа. Давайте попробуем расшифровать первые символы нашего сообщения.
Итак, сообщение начинается с единицы. С единицы у нас начинаются двоичные коды букв «М» и «А», посмотрев на следующий символ 0, мы можем точно определить, что первый символ – это буква «М». По такому же принципу мы можем определить, что, следующий символ буква «А» и до конца расшифровать слово «МАМА».
Следующая цифра – 0. С нуля у нас начинаются коды пяти символов. После него идёт так же 0. С 00 у нас начинается код пробела. Далее идёт буква «М». Следующая цифра – 0. С нуля у нас начинаются коды 5 символов. Возьмём следующую цифру. С 01 начинаются коды четырёх символов. Следующая цифра – 0. С 010 начинаются коды двух символов. Следующий символ – снова 0. И мы можем однозначно определить, что это буква «Ы». Так же расшифровывается и остальное сообщение.
Давайте посмотрим, двоичный код из скольких разрядов получился бы при использовании равномерного двоичного кодирования. Как мы помним сообщение записано с помощью алфавита мощностью 7 символов. Определим, разрядность двоичного кода, необходимую для кодирования одного символа такого алфавита. Как мы помним, для этого необходимо определить, в какую степень возвести цифру 2, чтобы получить 7. Но цифру семь мы так получить не можем, поэтому результат необходимо округлить в большую сторону. Мы можем так получить 8, для этого двойку нужно возвести в 3 степень. То есть для кодирования одного символа нам потребуется 3-разрядный двоичный код. Определим, какой код потребуется для кодирования всего сообщения, для этого нужно разрядность кода одного символа, то есть 3 умножить на длину всего сообщения, то есть 14. 3 × 14 = 42. То есть при кодировании сообщения нам потребовался бы 42-разрядный равномерный двоичный код. При использовании неравномерного кода нам потребовалось всего 36 разрядов, то есть на 6 разрядов меньше.
Сокращение длины двоичного кода заметно даже при небольшой длине сообщения. Если длина сообщения будет больше, например десятки тысяч символов, разница между длинами равномерного и неравномерного кода тоже увеличится. Когда длина двоичного кода составляет миллиарды разрядов – разница между равномерным и неравномерным кодом просто огромна.
Важно запомнить:
· Универсальность двоичного кодирования означает, что его можно применять для кодирования информации на любом формальном или неформальном языке, а также изображений и звука.
· Все коды можно разделить на равномерные и неравномерные, где равномерный код состоит из комбинаций равной длины, а неравномерный код состоит из комбинаций разной длины.
· Использование неравномерного кодирования позволяет сократить длину кода.

 Получите свидетельство
Получите свидетельство Вход
Вход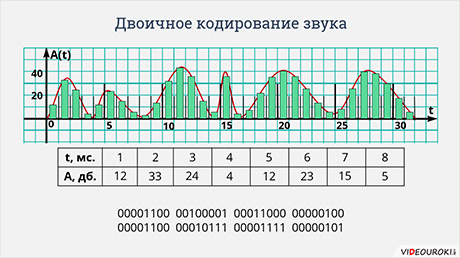




 14733
14733

