Получите свидетельство
Вход
На этом уроке мы вспомним, какой многоугольник называют правильным. Узнаем, каковы его элементы. А затем выведем формулы для вычисления элементов правильного многоугольника.
Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
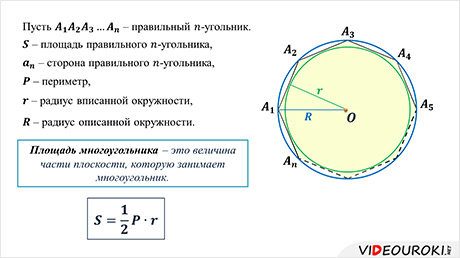
Пусть 
– правильный -угольник
– площадь правильного -угольника,
– сторона правильного -угольника,
– периметр,
– радиус вписанной окружности,
– радиус описанной окружности.
Площадь многоугольника – это величина части плоскости, которую занимает многоугольник.
Доказательство.
Для доказательства соединим центр многоугольника с его вершинами. Многоугольник разобьётся на n равных треугольников.
А значит, получим, что площадь правильного n-угольника равна половине произведения периметра правильного n-угольника на радиус вписанной в него окружности. Что и требовалось доказать.
Теперь давайте выведем формулы для вычисления стороны правильного многоугольника и радиуса вписанной окружности.
1. Пусть – правильный многоугольник.
– равнобедренный.
Рассмотрим 
.
– прямоугольный, т.к. 
– высота.
Следовательно,
.
2. Теперь докажем вторую формулу для вычисления стороны многоугольника через радиус описанной окружности
Пусть – правильный многоугольник.
– равнобедренный.
Рассмотрим .
– высота .
Следовательно,
– прямоугольный.
.
Что и требовалось доказать.
Радиус
вписанной окружности можно выразить через радиус описанной окружности по
следующей формуле: 
.
Пусть – правильный многоугольник.
– равнобедренный.
Рассмотрим .
– прямоугольный, т.к. – высота.
Следовательно,
.
Что и требовалось доказать.
Воспользовавшись формулой для вычисления стороны правильного n-угольника через радиус описанной окружности ,
давайте выразим формулы для нахождения стороны правильного треугольника,
квадрата и правильного шестиугольника. Соответственно, подставим в формулу
вместо n количество сторон указанных правильных
многоугольников 3, 4 и 6.
Задача. Радиус, описанной окружности около
правильного шестиугольника, равен 
см.
Найдите площадь правильного шестиугольника.
Решение.
(
)
(см)
(см)
(см)
Ответ: 
.
Подведем итоги урока. На этом уроке мы вывели формулы для вычисления элементов правильного многоугольника. Вспомним их:
Площадь правильного -угольника,
описанного около окружности, можно найти через периметр и радиус
вписанной окружности по формуле: 
Сторону правильного -угольника можно
выразить через радиус вписанной окружности:
Сторону правильного -угольника можно
выразить через радиус описанной окружности:
Радиус вписанной окружности можно
выразить через радиус описанной окружности по формуле:
А также мы с вами выразили формулы для вычисления
стороны правильного треугольника, квадрата и правильного шестиугольника
,
,
.
0
5498
