Окружность, вписанная в правильный многоугольник

На этом уроке мы вспомним, какую окружность называют вписанной в многоугольник. Докажем теорему об окружности, вписанной в правильный многоугольник. А также рассмотрим следствия из этой теоремы.

Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны. Так как у правильного многоугольника все углы равны, то угол правильного n-угольника можно вычислить по формуле: альфа энное равно 180 градусов умножить на эн минус два деленное на н, где n – количество сторон (углов) правильного n-угольника.

И вспомним еще определение вписанной окружности.

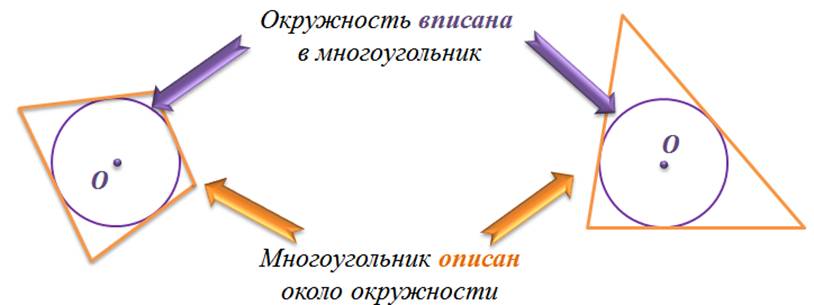
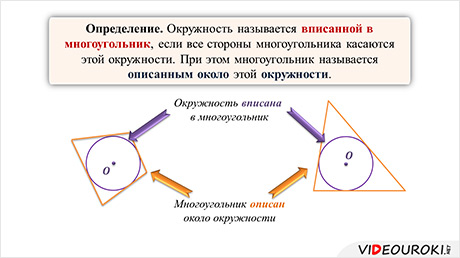
Определение. Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности. При этом многоугольник называется описанным около этой окружности.

Ранее мы с вами рассматривали касание прямой и окружности.

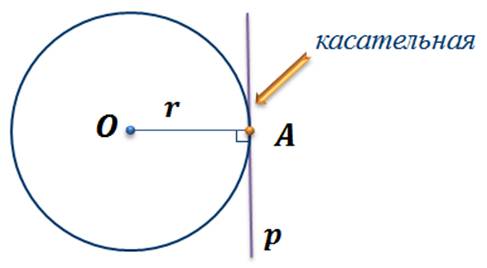
Напомню, что если задана окружность с центром в точке О и радиусом r, и точка А – общая точка прямой и окружности, то такая точка единственная. Прямая p, которая проходит через точку касания, называется касательной. Радиус OA, проведенный в точку касания, перпендикулярен касательной p.

Теорема. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

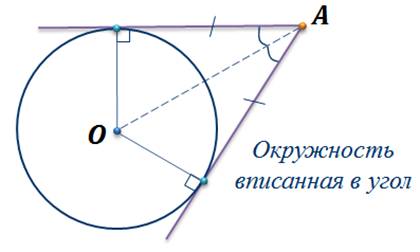
Значит, точка О – центр окружности – лежит на биссектрисе угла. Таким образом, имеем окружность, вписанную в угол.

Докажем теорему об окружности, вписанной в правильный многоугольник.

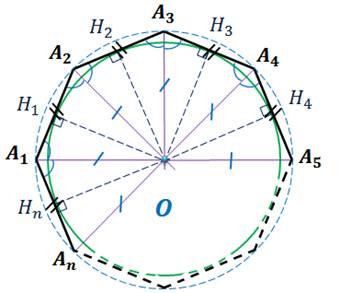
Теорема. В любой правильный многоугольник можно вписать                  окружность, и притом только одну.

Доказательство.

Пусть  – правильный многоугольник.

 по двум сторонам и углу между ними.

Отсюда,.

Т.е. .

Следовательно, точка  равноудалена от всех сторон многоугольника.

Если провести окружность с центром  и , то все стороны многоугольника будут касаться окружности в этих точках.

Значит, в данный многоугольник можно вписать окружность.

Теперь докажем, что вписанная окружность только одна.

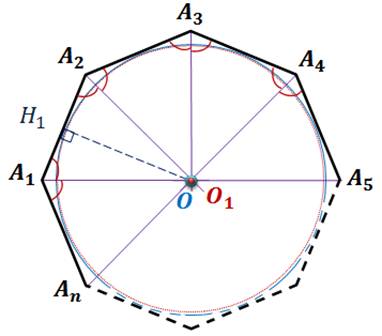
Предположим, что в то же время с окружностью с центром  и радиусом  существует и другая окружность.

Тогда ее центр  лежит на каждой из биссектрис углов многоугольника.

Следовательно, ее центр  совпадает с точкой  пересечения этих биссектрис.

Радиус этой окружности равен расстоянию от точки  до сторон многоугольника. Т.е. равен .Значит, вторая окружность совпадает с первой.

Теорема доказана.

Из этой теоремы вытекают следствия. Рассмотрим их.

Следствие 1. Окружность, вписанная в правильный многоугольник, касается                         сторон многоугольника в их серединах.

Доказательство.

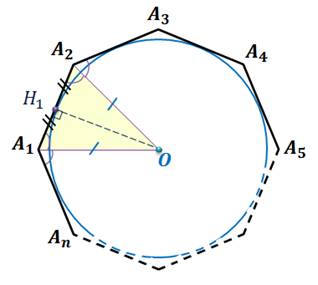
Пусть  – правильный многоугольник.

 – радиус вписанной в него окружности.

Рассмотрим .

Значит,  –  равнобедренный.

 –  по свойству касательной к окружности.

 –  высота .

 –  медиана  по свойствам равнобедренного треугольника.

Следовательно, .

Что и требовалось доказать.

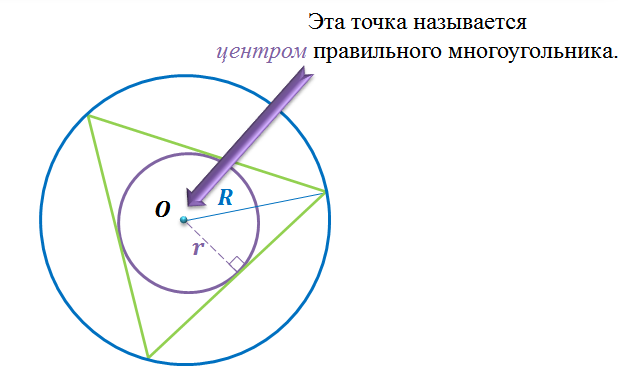
Следствие 2. Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.

Задача. В правильный четырехугольник вписана окружность. Определите ее радиус, если периметр правильного четырехугольника равен  см.

Решение.

Так как , то  – квадрат.

.

Значит,  (см).

 (см).

 (см).

Ответ:   (см).

Подведем итоги урока. На этом уроке мы доказали теорему об окружности, вписанной в правильный многоугольник. А именно, доказали, что в любой правильный многоугольник можно вписать окружность, и притом только одну. А также вывели следствия из этой теоремы. Первое следствие: окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. Второе  следствие: центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник. Эта точка называется центром правильного многоугольника.