В данной теме речь пойдёт о механической работе и мощности.
Механическая работа — это скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы. Под действием постоянной силы тело двигается прямолинейно и совершает перемещение в направлении действия силы, то сила совершает работу, равную произведению модуля этой силы и модуля перемещения.

Из определения следует единица измерения работы в метрической системе единиц

Эта единица названа в честь английского ученого Джеймса Прескотта Джоуля, впервые экспериментально обосновавшего эквивалентность работы и теплоты.
Это самый простой случай, когда перемещение тела и сила, действующая на него, совпадают по направлению.
Теперь рассмотрим, как вычисляется работа, когда направление действия силы не совпадает с направлением перемещения тела. Для этого рассмотрим следующий опыт. Через блок перекинута нить на которой висит брусок некоторой массы. На брусок действуют две силы — сила тяжести и сила натяжения нити.
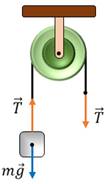
Если равномерно тянуть за нить, то тело будет равномерно двигаться, и, следовательно, результирующая сила, действующая на тело, будет равна нулю.
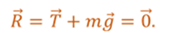
Значит, при некотором перемещении тела работа результирующей силы тоже будет равна нулю.

Однако сила натяжения нити совершает работу.

Поскольку при равномерном движении сила натяжения нити по модулю равна силе тяжести тела, то можно предположить, что сила тяжести совершает такую же работу по величине, но отрицательную.

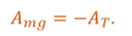
Отсюда можно сделать вывод: работа силы может быть положительной, отрицательной или равной нулю.
Заметим, что сила тяжести по направлению противоположна перемещению тела. Это обстоятельство и другие соображения позволяют предложить общую формулу для работы постоянной силы при равномерном прямолинейном движении. Если вектор силы и перемещения составляют между собой угол a, то работа этой силы равна произведению модуля силы на модуль перемещения и на косинус угла между ними.

Это и есть общее выражение для работы постоянной силы.
Из этой формулы видно, что в случае, когда угол между направлением вектора силы и вектора перемещения острый, то косинус этого угла будет больше нуля и, следовательно, больше нуля будет работа силы.

Если вектор силы и вектор перемещения составляют между собой тупой угол, то значение косинуса этого угла меньше нуля. Значит и работа этой силы будет отрицательна.

И, наконец, если вектор силы перпендикулярен вектору перемещения, то работа не совершается (вернее, работа этой силы равна нулю).

Если к движущемуся телу приложено несколько сил, то каждая из них совершает работу, а общая работа равна алгебраической сумме работ, совершаемых отдельными силами.
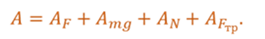
Работу, совершенную силой, можно найти и графически. Так, если действие силы на тело не меняется с течением времени и совпадает по направлению с перемещением, то работа этой силы численно равна площади заштрихованного прямоугольника.
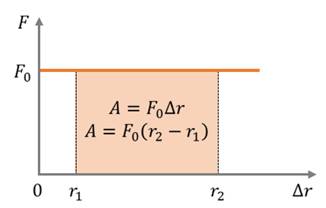
Если же сила изменяется в процессе движения, то работа этой силы тоже будет численно равна площади под кривой. В частности, на рисунке представлен график силы, которая линейно уменьшается с пройденным расстоянием до нуля. Очевидно, что работа этой силы на пройденном пути, численно равна площади треугольника.
Ранее говорилось, что основными силами в механике являются гравитационные силы (в частности сила тяжести), силы упругости и силы трения.
Проанализируем более подробно работы, совершаемые каждой из этих сил. Начнем с работы силы тяжести. Будем ее рассматривать считая, что тело находится на небольших расстояниях от поверхности Земли. В этом случае сила тяжести будет постоянной по модулю равной

Пусть тело массой m падает с некоторой высоты h1 до высоты h2. Тогда модуль перемещения тела равен разности этих высот
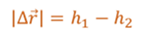
Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна произведению модуля силы тяжести и разности высот.

Следует помнить, что высоты, на которых находится тело, можно отсчитывать от любого уровня. Это может быть уровень поверхности Земли, пола или поверхности стола. Высоту выбранного уровня принимают равной нулю. Поэтому этот уровень называют нулевым. Так, если тело падает с высоты h до нулевого уровня, то работа силы тяжести равна

Теперь выясним, какую работу совершает сила тяжести, если тело движется не по вертикали. Для этого рассмотрим движение тела по наклонной плоскости.
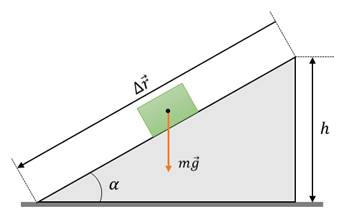
Пусть тело некоторой массы m совершило перемещение, равное по модулю длине наклонной плоскости. Работа силы тяжести в этом случае равна

Из рисунка видно, что

Поэтому работа силы тяжести в этом случае также равна
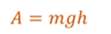
Таким образом, получили для работы силы тяжести такое же выражение, как и в случае движения тела по вертикали. Отсюда следует главный вывод о том, что работа силы тяжести не зависит от того, по какой траектории движется тело и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях тела.
Тогда очевидно, что если тело движется по замкнутой траектории, где начальное и конечное положения тела совпадают, то работа силы тяжести равна нулю. Напомним, что такие силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным положениями тела в пространстве, называются потенциальными или консервативными. Следовательно, сила тяжести — это консервативная сила.
Теперь проанализируем работу, совершаемую силой упругости. Сила упругости — это сила, возникающая при деформации тела внешними воздействиями.
Рассмотрим систему, состоящую из пружины и тела некоторой массы, лежащего на достаточно гладкой горизонтальной поверхности. Левый конец пружины прикреплен к стене, а правый — к телу. Направим ось икс так, как показано на рисунке.
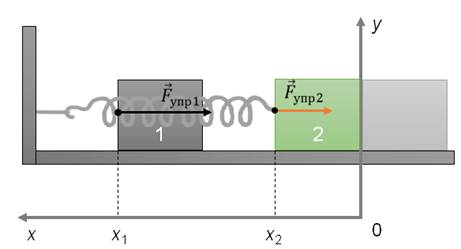
Если тело сместить на некоторое расстояние от положения равновесия, то пружина будет действовать на него с силой упругости, направленной вправо. Модуль проекции этой силы на ось Ox будет определяться на основании закона Гука.
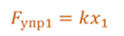
Теперь отпустим тело. Тогда под действием силы упругости пружины тело будет смещаться вправо.
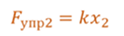
При этом сила упругости будет совершать работу. Предположим, что тело переместилось так, что расстояние от положения равновесия стало х2. Очевидно, что тогда модуль перемещения тела равен разности между начальной и конечной координатой тела.
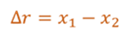
Для нахождения работы, совершенной пружиной по перемещению тела, необходимо учесть, что сила упругости меняется, так как ее величина зависит от удлинения пружины. Воспользуемся графиком зависимости модуля силы упругости от удлинения пружины.
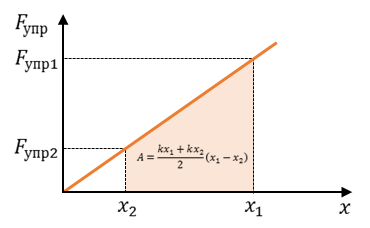
Известно, что работа силы численно равна площади под графиком силы. В рассматриваемом случае это площадь трапеции, основаниями которой являются силы упругости пружины в положении один и два, а высота — это перемещение тела.
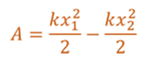
Из полученной формулы следует, что работа силы упругости пружины зависит только от координат начального и конечного положений. Из рисунка видно, что х1 и х2 — это и удлинение пружины, и координаты ее конца в выбранной системе координат. Следовательно, работа силы упругости не зависит от формы траектории. А если траектория замкнута, то работа равна нулю. Таким образом, сила упругости является потенциальной силой.
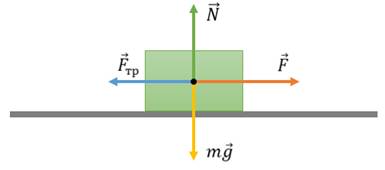
И проанализируем работу, совершаемую силой трения. Рассмотрим тело, находящееся на некоторой поверхности (например, брусок на поверхности стола).
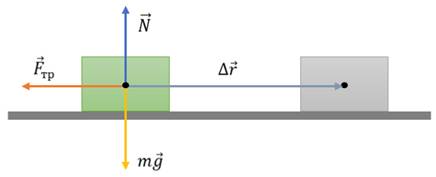
Если толкнуть брусок, то он придет в движение, однако, через некоторое время, остановится. В процессе движения бруска на него действуют: сила тяжести, сила нормальной реакции опоры и сила трения скольжения. Под действием этих трех сил и движется брусок. Поскольку сила тяжести компенсируется силой нормальной реакции стола, то равнодействующая сила равна действующей на брусок силе трения. А так как сила трения направлена противоположна перемещению, то работа этой силы будет отрицательной (так как косинус ста восьмидесяти градусов равен минус единице).
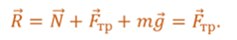

Из формулы следует, что работа силы трения зависит от модуля перемещения тела. И даже если тело вернется в исходную точку, то работа силы трения не будет равна нулю. Такие силы, работа которых зависит от формы траектории движения тела и на замкнутой траектории отличны от нуля, называются непотенциальными или диссипативными (от латинского — рассеяние).
Однако не надо думать, что работа сил трения всегда отрицательна. Ведь именно благодаря силе трения покоя человек и различные машины движутся по Земле. Действительно, при ходьбе человек действует на поверхность Земли с некоторой силой F1 (кроме силы нормальной реакции), а по третьему закону Ньютона Земля действует на ногу человека с силой трения покоя, равной по модулю силе воздействия человека, но противоположно направленной. Благодаря этой силе человек движется. Сила трения покоя направлена также, как и скорость человека, и, следовательно, работа этой силы положительна.
Таки образом, были рассмотрены работы основных трех сил, с которыми чаще всего мы сталкиваемся в механике. Однако, одна и та же работа в разных случаях может быть выполнена за различные промежутки времени, то есть она может совершаться неодинаково быстро. Очевидно, что чем меньшее времени требуется для выполнения данной работы, тем эффективнее работает машина, механизм и прочее.
Величина, характеризующая быстроту совершения работы, и равная отношению работы, совершаемой силой, к промежутку времени, в течение которого она совершается, называется мощностью.
Исходя из определения видим, что единицей измерения мощности является
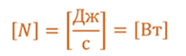
Эта единица получила название Ватт, в честь английского ученого Джеймса Уатта — изобретателя универсального парового двигателя.
При движении любого тела на него в общем случае действует несколько сил, каждая из которых совершает работу и, следовательно, для каждой силы можно вычислить мощность. Так, если тело движется прямолинейно и на него действует постоянная сила, то она совершает работу, равную

Тогда мощность силы равна отношению работы этой силы к промежутку времени.

Мощность силы также равна произведению модуля силы на модуль скорости и на косинус угла между направлениями вектора силы и вектора скорости.
По записанной формуле можно рассчитывать и среднюю, и мгновенную мощности, подставляя значение средней или мгновенной скорости.
Из полученной формулы следует, что при заданной мощности мотора сила тяги тем меньше, чем больше скорость движения. Вот почему водители автомобилей при подъеме в гору, когда нужна наибольшая сила тяги, переключают двигатель на пониженную передачу.
И так, любой двигатель или механическое устройство предназначены для выполнения определенной механической работы. Эта работа называется полезной работой. Для двигателя автомобиля — это работа по его перемещению, для токарного станка — работа по вытачиванию детали.
Однако в любой машине, в любом двигателе полезная работа всегда меньше той энергии, которая затрачивается для приведения их в действие, потому что всегда существуют силы трения, работа которых приводит к нагреванию каких-либо частей устройства. А нагревание нельзя считать полезным результатом действия машины. Поэтому каждое устройство характеризуется особой величиной, которая показывает, насколько эффективно используется подводимая к нему энергия. Эта величина называется коэффициентом полезного действия и обычно обозначается греческой буквой h.
И так, коэффициентом полезного действия называется отношение полезной работы, совершенной машиной за некоторый промежуток времени, ко всей затраченной работе (или подведенной энергии) за тот же промежуток времени.
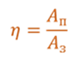
Коэффициент полезного действия обычно выражается в процентах. Поскольку и полезную, и затраченную работы можно представить, как произведение мощности на промежуток времени в течение которого работала машина, то



Основные выводы:
Рассмотрели важную физическую величины – работу. Рассмотрели работы наиболее часто встречающихся сил — силы тяжести, упругости и силы трения. Повторили понятие мощности, а также вспомнили, что называют коэффициентом полезного действия механизма.

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 16264
16264

