«Свет… такое короткое и
в то же время такое ёмкое слово.
В слове «свет» заключена вся физика».
С.И. Вавилов
В данном уроке речь пойдёт о дифракции света, еще одном явлении, которое присущее только волновым процессам.
В прошлой теме рассмотрели явление интерференции света, т.е. явления наложения световых когерентных волн, в результате которого наблюдается устойчивая во времени картина чередования максимумов и минимумов интенсивности света.
Были выведены условия интерференционных максимумов и минимумов. Было установлено, что явление интерференции присуще только волновым процессам.
Но, если свет — это волна, то помимо явления интерференции света, должно также наблюдаться и явление дифракции — огибание волнами препятствий. Тени от мелких предметов выглядят достаточно резко. Как же тогда пронаблюдать явление дифракции, если оно действительно существует? Для этого рассмотрим тень иглы с помощью видеокамеры на экране телевизора, поставив перед источником света узкую щель. Видно, что снаружи тень окаймлена радужными полосками, а в середине появилась светлая полоса.
Еще опыт. Перед источником света поставим преграду — круглый металлический шарик, а вместо щели возьмем треугольное отверстие. Теперь в центре тени появилось светлое пятно треугольной формы. Значит, за непрозрачной преградой видно изображение источника света. Свет, как бы проникает внутрь тени, огибая при этом препятствие.
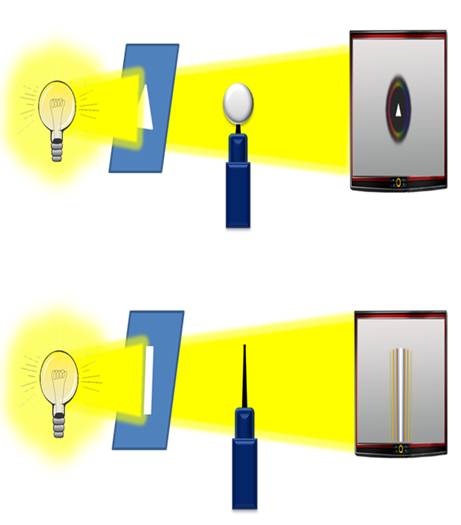
Это явление и называют дифракцией света.
И так, дифракцией света называется совокупность оптических явлений, обусловленных волновой природой света и наблюдающихся при его распространении в среде с резко выраженными неоднородностями. В результате происходит огибание волнами препятствий, размеры которых соизмеримы с длиной волны.
Впервые на эту особенность обратил внимание Леонардо Да Винчи. Гримальди подробно описал ее в 1665 году. Но лишь в начале 19 века нашел этому явлению объяснение французский физик Огюст Френель. Френель писал работу на конкурс, организованный Академией наук Франции, где им были изучены явления интерференции и дифракции света.
В начале, в своих работах, Френель пытался объяснить явление дифракции с помощью принципа Гюйгенса, согласно которому, как мы уже знаем, каждая точка, до которой доходит волна, является центром вторичных сферических когерентных волн, а огибающая этих волн дает положение нового фронта волны в следующий момент времени. Однако, как оказалось, с помощью данного принципа можно решить задачу о направлении распространения волнового фронта, но нельзя выяснить, от чего же зависит амплитуда, а, как следствие, и интенсивность волн, распространяющихся по разным направлениям. Поэтому Френелю пришлось развить этот принцип дальше, дополнив его идеей об интерференции вторичных волн. Таким образом, принцип Гюйгенса трансформировался в принцип Гюйгенса-Френеля, согласно которому, каждая точка фронта волны является источником вторичных сферических когерентных волн. При этом новый фронт волны образуется как раз за счет интерференции вторичных волн.
Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду, а, следовательно, и интенсивность результирующей волны в любой точке пространства.
Рассмотрим опыты по дифракции света на круглом отверстии. В качестве источника монохроматического света возьмем лазер. При изменении расстояния диафрагмы от экрана в области тени происходит перераспределение света.
Как это объяснить? По волновой теории Гюйгенса, каждая точка волнового фронта становится источником вторичных волн. Интерферируя, эти вторичные волны и создают наблюдаемую картину на экране. А теперь будем менять размеры диафрагмы.
В центре картины светлое пятно.
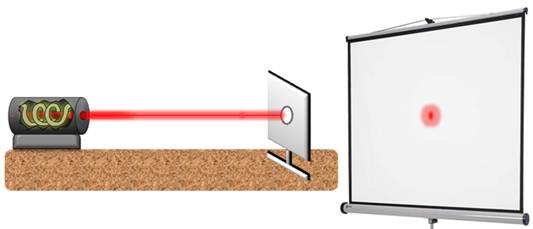
Теперь темное.
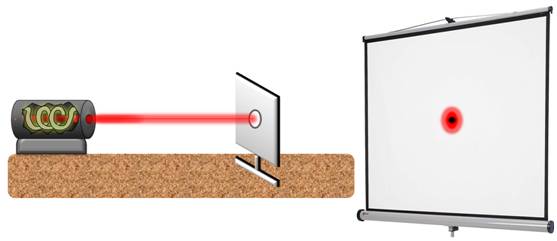
И снова светлое.
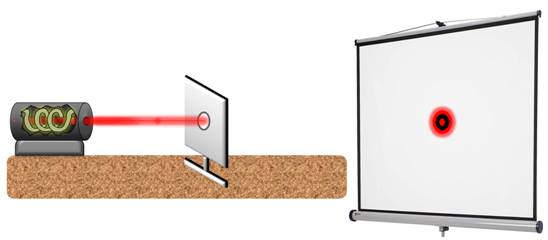
Как можно заметить, изменяется и сама дифракционная картина.

Для объяснения полученной дифракционной картины от круглого отверстия, Френель предложил разбить волновую поверхность на отдельные кольцевые зоны так, чтобы расстояние от соседних зон до точки наблюдения отличались на половину длины волны. Размер диафрагмы ограничивает число действующих зон. В нашем случае, освещенность будет зависть только от действия первой и второй зон. При этом волны от этих зон будут приходить к экрану в противофазе и, следовательно, гасить друг друга. Поэтому в центре дифракционной картины мы наблюдаем темное пятно. Если же мы увеличим отверстие так, чтобы на освещенность экрана влияла еще и третья зона, то в центре появится светлое пятно. Следует учесть, что с увеличением номера зоны будет уменьшаться угол, под которым она видна из точки наблюдения. Вследствие этого уменьшаются и амплитуды волн.
Амплитуда волны в центре дифракционной картины определяется полу суммой волн от первой и последней открытой зоны, когда их число нечетное. И их полу разностью при четном числе зон.

Любопытно отметить, что если оставить открытой только одну первую зону, то амплитуда увеличится в два, а интенсивность в 4 раза, по сравнению с действием всех зон. Таким образом, отверстие, шириной в одну зону Френеля обладает фокусирующим действием.
Еще больший эффект получим, оставив только четные или только нечетные зоны. На этом принципе устроена зонная пластинка Френеля, действующая подобно линзе.
Все свои идеи и расчеты Френель изложил в конкурсной работе по исследованию световых явлений, которую направил в Академию наук Франции и получил за нее главный приз.
Но самое интересное произошло дальше. Рассматривая расчеты Френеля, член комиссии Пуассон заметил, что они приводят к парадоксальному результату: согласно Френелю за большим круглым непрозрачным телом прямо в середине его геометрической тени должно возникать небольшое светлое пятно. Очевидную абсурдность этого результата Пуассон хотел использовать как главный аргумент против теории дифракции Френеля, однако, Доминик Араго поставил эксперимент, подтвердивший это предсказание. В итоге полученный результат, ставший известным как пятно Араго — Пуассона, оказался весомым аргументом в пользу новой волновой теории.
В наши дни важную роль в прикладной оптике играют явления дифракции на отверстиях в форме щели с параллельными краями. Но использование дифракции света на одной щели затруднено из-за очень слабой видимости дифракционной картины. Выходом из этой трудной ситуации стало создание дифракционной решетки. Дифракционная решетка — это спектральный прибор, служащий для разложения света в спектр и измерения длины волны. Она представляет собой совокупность большого числа параллельных штрихов одинаковой формы, нанесенных на плоскую или вогнутую полированную поверхность на одинаковом расстоянии друг от друга.

Рассмотрим плоскую прозрачную дифракционную решетку. Обозначим ширину прозрачного штриха через a, а ширину непрозрачного промежутка через b.
Сумму ширины прозрачного участка и ширины непрозрачного промежутка называют постоянной (или периодом) дифракционной решетки. Она также обратно пропорциональна числу штрихов на единицу длины решетки.
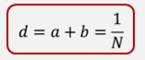
Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Тогда, согласно принципа Гюйгенса-Френеля, каждая щель будет являться источником вторичных волн, способных интерферировать друг с другом. Если за дифракционной решеткой установить линзу, то в ее фокальной плоскости можно будет наблюдать дифракционную картину.
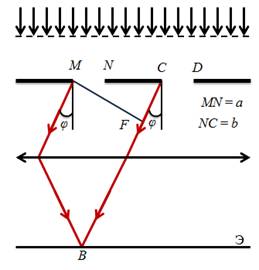
Допустим, что свет дифрагирует на щелях под некоторым углом. Из-за того, что щели находятся на одинаковом расстоянии друг от друга, разности хода лучей, идущих от двух соседних щелей, для данного направления будут одинаковыми в пределах всей дифракционной решетки.
В
тех направлениях, для которых разность хода равна четному числу полуволн, будет
наблюдаться интерференционный максимум. И, наоборот, для тех направлений, где
разность хода равна нечетному числу полуволн, наблюдается интерференционный
минимум. Тогда, в направлениях, для которых углы 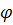 будут
удовлетворять условию
будут
удовлетворять условию
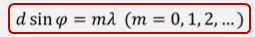
Эту формулу часто называют формулой дифракционной решетки. В ней m — это порядок главного максимума.
Если наблюдать дифракцию в белом свете, то можно заметить, что все главные максимумы, кроме центрального нулевого, будут окрашены. Это и понятно, ведь различным длинам волн соответствуют различные углы, на которых наблюдаются интерференционные максимумы.
В настоящее время оптические приборы с дифракционными решетками получили широкое распространение, как физике, астрономии, так и в химии, биологии, технике. С их помощью изучаются спектры отражения и поглощения веществ, оптические свойства различных материалов. Благодаря дифракции света нам удалось глубже проникнуть в удивительный мир живых клеток, расширить наши познания о далеком прошлом и настоящем нашей вселенной.

Основные выводы:
– Дифракцией света называется совокупность оптических явлений, обусловленных волновой природой света и наблюдающихся при его распространении в среде с резко выраженными неоднородностями. В результате происходит огибание волнами препятствий, размеры которых соизмеримы с длиной волны.
– Явление дифракции легко объясняется на основании принципа Гюйгенса-Френеля, согласно которому, каждая точка фронта волны является источником вторичных сферических когерентных волн.
– Дифракционная решетка — это спектральный прибор, служащий для разложения света в спектр и измерения длины волны. Она представляет собой совокупность большого числа параллельных штрихов одинаковой формы, нанесенных на плоскую или вогнутую полированную поверхность на одинаковом расстоянии друг от друга.
– Выведена формула, по которой можно рассчитать положения главных максимумов в дифракционной картине, полученной с помощью дифракционной решетки.

 Получите свидетельство
Получите свидетельство Вход
Вход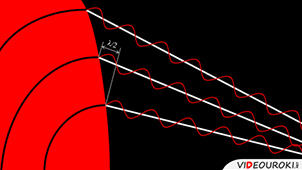



 0
0 8908
8908


