Определение расстояний до звёзд. Видимая и абсолютная звёздные величины

Наше Солнце справедливо называют типичной звездой. Но среди большого и разнообразного числа звёзд есть немало таких, которые значительно отличаются от него по своим физическим характеристикам и химическому составу. Поэтому полное представление о звёздах даст такое определение:

Звезда — это массивный газовый шар, излучающий свет и удерживаемый в состоянии равновесия силами собственной гравитации и внутренним давлением, в недрах которого происходят (или происходили ранее) реакции термоядерного синтеза.

Мысли о том, что звёзды — это далёкие солнца, высказывались ещё в глубокой древности. Но из-за колоссальных расстояний до них диски звёзд не видны даже в самые мощные телескопы. Поэтому, чтобы найти возможность сравнивать звёзды между собой и с Солнцем, необходимо было придумать способы определения расстояний до них.

Ещё Аристотель предполагал, что если Земля движется вокруг Солнца, то, наблюдая за звездой из двух диаметрально противоположных точек земной орбиты, можно заметить изменение направления на звезду — её параллактическое (то есть кажущееся) смещение.

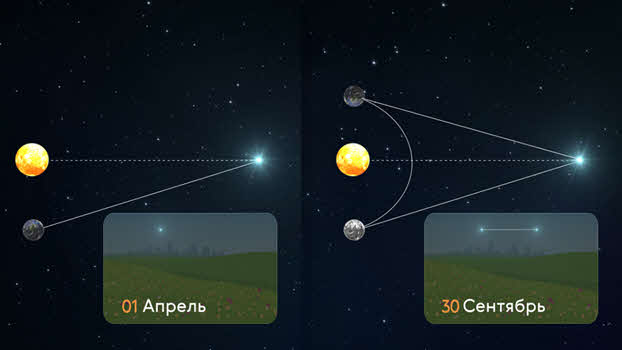
Такая же идея измерения расстояний была предложена и Николаем Коперником после опубликования им гелиоцентрической системы мироустройства. Однако ни Копернику, ни тем более Аристотелю не удалось обнаружить это смещение.

Лишь к середине XIX века, когда на телескопы стали ставить оборудование для точного измерения углов, удалось измерить такое смещение у ближайших звёзд. Как удалось установить, кажущееся перемещение более близкой звезды на фоне очень далёких звёзд происходит по эллипсу с периодом в один год и отражает движение наблюдателя вместе с Землёй вокруг Солнца. Этот небольшой эллипс, который описывает звезда, называется параллактическим эллипсом.

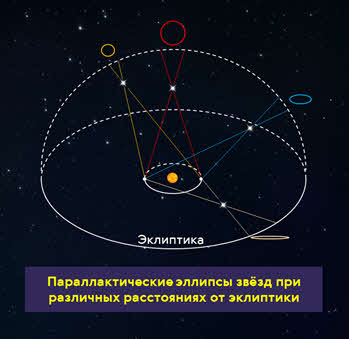
В угловой мере его большая полуось равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом и обозначается греческой буквой π или латинской буквой р.

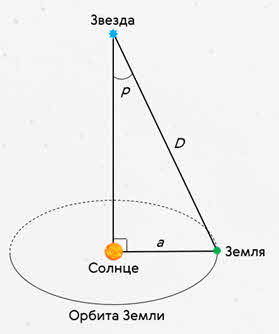
Зная годичное параллактическое смещение звезды, можно легко определить расстояние до неё:

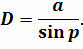
В записанной формуле а — это средний радиус земной орбиты.

Если учесть, что годичные параллаксы звёзд измеряются десятитысячными долями секунды, а большая полуось земной орбиты равна одной астрономической единице, то можно получить формулу для вычисления расстояния до звезды в астрономических единицах:

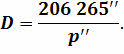
Первые надёжные измерения годичного параллакса были осуществлены почти одновременно в Германии, России и Англии в 1837 году.

В России первые измерения годичного параллакса были проведены Василием Яковлевичем Струве для яркой звезды Северного полушария Веги. Давайте по его данным определим расстояние до этой звезды.

Согласитесь, что для измерения расстояний до звёзд астрономическая единица слишком мала. Даже ближайшая к нам звезда — альфа-Центавра — расположена более чем в 273,5 тысячах а. е. Поэтому для удобства определения расстояний до звёзд в астрономии применяется специальная единица длины — парсек (сокращённо пк), название которой происходит от двух слов — «параллакс» и «секунда».

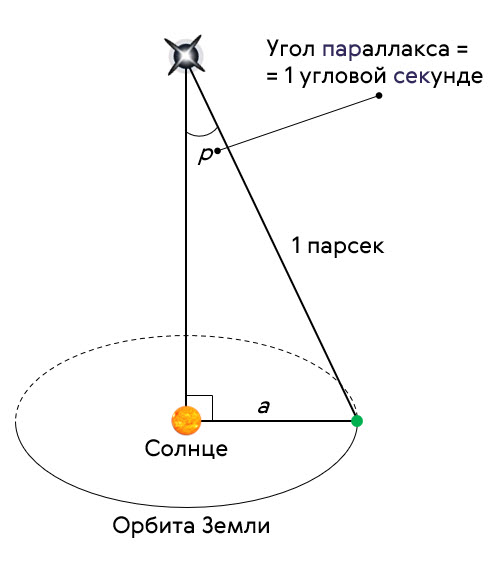
Парсек — это расстояние, с которого средний радиус земной орбиты, перпендикулярный лучу зрения, виден под углом в одну угловую секунду:

1 пк = 206 265 а. е. =30,8586 трлн км.

Исходя из определения, расстояние в парсеках равно обратной величине годичного параллакса:

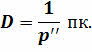
Вернёмся к нашей задаче и определим расстояние до Веги в парсеках, воспользовавшись полученным нами уравнением.

Также, помимо парсека, в астрономии используется ещё одна внесистемная единица измерения расстояний — световой год.

Световой год — это расстояние, которое свет, распространяясь в вакууме, проходит за один год:

1 пк = 3,26 св. г. = 206 265 а. е. = 3 ∙ 10¹³ км.

В 1989 году Европейским космическим агентством был запущен спутник «Гиппаркос». За 37 месяцев своей работы ему удалось измерить годичные параллаксы более чем миллиона звёзд. При этом точность измерений для более ста тысяч из них составила одну угловую миллисекунду.

Однако после того, как астрономы научились определять расстояния до звёзд, возникла ещё одна проблема. Оказалось, что звёзды, находящиеся примерно на одинаковом расстоянии от Земли, могут отличаться друг от друга по видимой яркости (блеску). При этом видимый блеск не характеризует реального излучения звезды. Например, Солнце нам кажется самым ярким объектом на небе лишь потому, что оно находится гораздо ближе к Земле, чем остальные звёзды. Поэтому для сравнения истинного блеска звёзд необходимо было определять их звёздную величину на определённом одинаковом расстоянии от Земли. За такое одинаковое (или стандартное) расстояние принято 10 пк. Видимая звёздная величина, которую имела бы звезда, если бы находилась от нас на расстоянии 10 пк, называется абсолютной звёздной величиной.

Почему в качестве эталонного расстояния было выбрано 10 парсек? Да для простоты расчётов. Итак, предположим, что видимая звёздная величина звезды на некотором расстоянии D равна т а её блеск — I.

Напомним, что блеск двух источников, звёздные величины которых отличаются на единицу, отличаются в 2,512 раза. То есть для двух звёзд, звёздные величины которых равны т₁ и т₂ соответственно, отношение их блесков выражается соотношением:

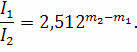
Тогда по определению видимая звёздная величина звезды с расстояния в 10 пк будет равна абсолютной звёздной величине М. Если обозначить блеск звезды на этом расстоянии через I₀, то для видимой и абсолютной звёздных величин одной и той же звезды предыдущее уравнение будет выглядеть так:

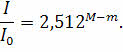
В тоже время из физики известно, что блеск меняется обратно пропорционально квадрату расстояния:

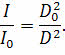
Подставим данное выражение в предыдущее уравнение, при этом учтём, что :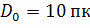

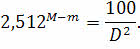
Теперь прологарифмируем полученное выражение:

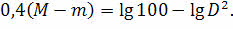
И упростим его:

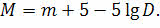
Если учесть, что расстояние до звезды обратно пропорционально её годичному параллаксу, то получим формулу, по которой можно вычислить абсолютную звёздную величину близко расположенных к нам звёзд

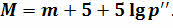
Теперь давайте по полученной формуле рассчитаем абсолютную звёздную величину нашего Солнца. Для этого учтём, что его видимая звёздная величина равна–26,8^т, а среднее расстояние до него составляет одну астрономическую единицу

То есть наше Солнце выглядит слабой звёздочкой почти пятой звёздной величины.

Зная абсолютную звёздную величину звезды, можно вычислить её действительное общее излучение или светимость.

Светимостью называют полную энергию, излучаемую звездой за единицу времени. Светимость звезды можно выразить в ваттах, но чаще её выражают в светимостях Солнца.

Используя формулу Погсона, можно записать соотношение между светимостями и абсолютными звёздными величинами какой-либо звезды и Солнца:

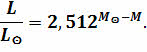
Данную формулу можно переписать, если учесть, что светимость Солнца принята за единицу, а его абсолютна звёздная величина равна 4,8^m:

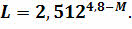
По светимости (то есть мощности излучения) звёзды значительно отличаются друг от друга. Так мощность излучения некоторых звёзд-сверхгигантов больше мощности излучения Солнца в 330 тыс. А некоторые звёзды-карлики, обладающие наименьшей светимостью, излучают свет в 480 тыс. раз слабее нашего Солнца.