Интерференция, дифракция и поляризация механических волн

Очень часто в среде одновременно распространяется не одна, а несколько различных волн. Так, например, если мы бросим в воду два камня, образовав тем самым две круговые волны. Однако посмотрите, каждая волна проходит сквозь другую и ведёт себя в дальнейшем так, как будто другой волны совсем не существовало.

Теперь посмотрим более внимательно, что происходит в местах, где волны накладываются одна на другую. Наблюдая волны на поверхности воды от двух брошенных в воду камней, можно заметить, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если две волны встречаются в одном месте своими гребнями, то в этом месте возмущение поверхности воды усиливается. Если же, напротив, гребень одной волны встречается с впадиной другой, то поверхность воды не будет возмущена.

Вообще же в каждой точке среды колебания, вызванные двумя волнами, просто складываются.

Сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний частиц среды, называется интерференцией.

Выясним, при каких условиях наблюдается интерференция волн. Для этого будем непрерывно создавать волны на поверхности воды в двух каких-нибудь её точках. Для этого в непосредственной близости к поверхности воды поместим концы двух проволочек, приделанных к упругой металлической пластинке.

При колебании пластинки концы проволочек будут периодически погружаться в воду и возбуждать колебания, распространяющиеся в виде волн одинаковой длины по её поверхности. Каждая из проволочек возбуждает свою систему волн. Две системы волн, налагаясь одна на другую, будут взаимодействовать. В результате на поверхности воды возникает определённое, неизменное во времени распределение амплитуд колебаний, которое называют интерференционной картиной.

Для дальнейшего важно, чтобы две системы волн были согласованы, то есть чтобы при одинаковой длине они выходили из центров колебания в одинаковых фазах. Такие волны называются когерентными.

В данном опыте когерентность обеспечена тем, что оба конца проволоки периодически касаются поверхности воды одновременно — волны оставляют центры колебания в одинаковых фазах.

В любой точке на поверхности воды будут складываться колебания, вызванные двумя волнами. Однако результат сложения этих волн, приходящих в данную точку, зависит от разности фаз между ними. Для решения вопроса о том, в каких фазах встретятся в данной точке интерферирующие волны, нужно учесть разность хода этих волн. Пусть нас интересует результат наложения волн в точке, находящейся на расстоянии r₁ от первого источника волн и на расстоянии r₂ от второго источника.

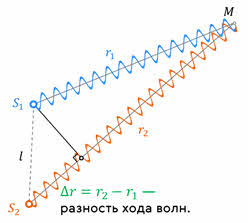
Расстояние Δr = r₂ – r₁, называется разностью хода волн. Если источники волн колебались в одинаковых фазах, то при разности хода, равной целому числу длин волн или чётному числу полуволн, в данную точку волны будут приходить в одинаковых фазах и при сложении их в этой точке возникает усиление колебаний:

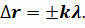
Если разность хода окажется равной нечётному числу полуволн, то волны от источников придут в эту точку в противоположных фазах и в ней произойдёт ослабление колебаний:

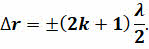
Когда мы с вами только начинали изучать волновое движение, мы говорили о том, что в процессе распространения волн происходит перенос энергии без переноса вещества. Возникает логичный вопрос, что происходит с этой энергией при гашении волн друг другом? Может быть, она превращается в другие формы, и в минимумах интерференционной картины выделяется тепло? Оказывается нет. Наличие минимума в данной точке интерференционной картины означает, что энергия сюда совсем не поступает. Вследствие интерференции происходит перераспределение энергии в пространстве. Она не распределяется равномерно по всем частицам среды, а концентрируется в максимумах за счёт того, что в минимумы не поступает вовсе.

Ярким примером интерференции волн служит стоячая волна. Для её получения возьмём нить, один конец которой привязан к молоточку звонка, а к другому концу через блок подвешена маленькая гирька.

Частицы нити передают друг другу колебания от молоточка, и волна распространяется до блока, вызывая вынужденные колебания груза. Эти колебания порождают отражённую волну той же частоты. Таким образом, каждая точка нити участвует в двух колебаниях, которые приходят с разных сторон. Если изменять расстояние от молоточка до блока, то можно наблюдать, как при некоторых расстояниях возникают стоячие волны.

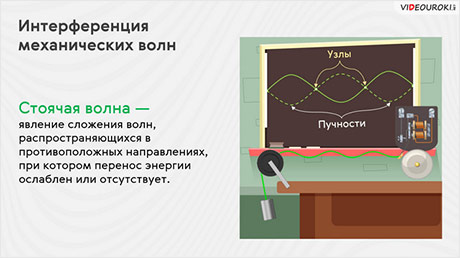
Стоячая волна — это вид волнового движения, происходящий без переноса энергии.

Такое название возникло потому, что при распространении таких волн нет перемещения фазы между колеблющимися точками, а некоторые из точек стоячей волны совсем не колеблются. Точки стоячей волны, которые не колеблются, называются узлами. Расстояние между соседними узлами составляет половину длины стоячей волны. А точки стоячей волны, амплитуды которых максимальны, называются пучностями.

Запишем уравнения прямой и обратной волны:

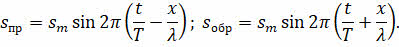
При наложении происходит сложение этих волн:

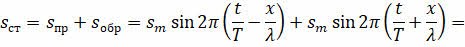
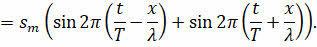
Упростим полученное выражение, вынеся общий множитель за скобки.

Далее воспользуемся формулой суммы синусов, знакомой вам из математики:  

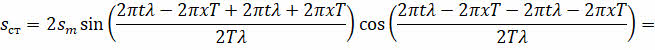
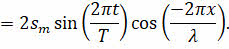
В силу чётности функции косинуса, а также помня о том, что отношение 2π/Т — это циклическая частота, получим уравнение стоячей волны:

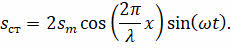
Из него видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и во встречных волнах. А амплитуда колебаний при возбуждении стоячей волны зависит от положения колеблющейся точки, то есть определяет амплитуду колебаний в некоторой точке с координатой х.

В точках, находящихся на расстоянии целого числа длин полуволн, колебания происходят с удвоенной амплитудой, то есть наблюдаются интерференционные максимумы или пучности стоячей волны.

В точках же, находящихся на расстоянии нечётного числа четвертей волн, колебания вовсе не происходят. Здесь мы наблюдаем интерференционный минимум или узел.

В таблице приведено сравнение стоячей и бегущей волн:

Рассмотрим возбуждение стоячей волны в струне, закреплённой с двух концов. Очевидно, что точки закрепления будут являться узлами стоячей волны. Самая большая длина волны, возбуждаемая в струне, будет при условии, что её длина равна половине длины волны:

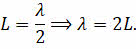
Такая длина волны соответствует самой низкой частоте, то есть основному музыкальному тону. Увеличивая частоту в целое число раз, мы можем получить первый, второй и так далее обертоны.

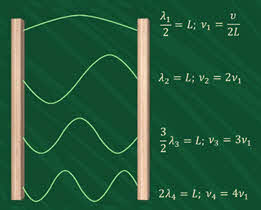
Частоты, при которых возникают стоячие волны, называются собственными или резонансными частотами.

Теперь давайте возьмём две одинаковые струны и поместим их на некотором расстоянии друг от друга одна под одной. Заставив нижнюю струну колебаться, мы заметим, как верхняя струна также начинает звучать. Это явление получило название акустического резонанса.

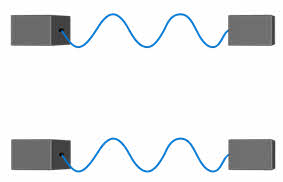
Таким образом, акустическим резонансом называется явление возрастания амплитуды звуковой волны в системе при приближении частоты источника, возбуждающего в ней колебания, к собственной частоте колебаний системы.

Теперь давайте проведём такой опыт. Получим в ванне на поверхности воды систему волн и ограничим их дальнейшее распространение отверстием, ширина которого в несколько раз больше длины волны. Не трудно увидеть, что за отверстием волны распространяются в области, ограниченной прямыми линиями, перпендикулярными к поверхности падающих волн. Только на сравнительно большом расстоянии от отверстия волны, слегка загибаясь, заходят за эти прямые.

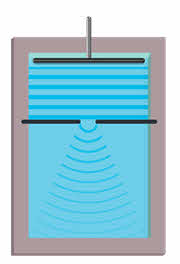
Сузим ограничивающее отверстие до размера, меньшего длины волны падающих волн. Область за отверстием окажется заполненной круговыми волнами, как если бы в отверстии экрана находился источник волн — наблюдается дифракция волн.

Дифракцией называется явление огибания волнами препятствий, соизмеримых с длиной волны.

Это можно объяснить принципом Гюйгенса. Согласно ему каждая точка фронта (поверхности, достигнутой волной) является вторичным (то есть новым) источником сферических волн. Огибающая фронтов волн всех вторичных источников становится фронтом волны в следующий момент времени.

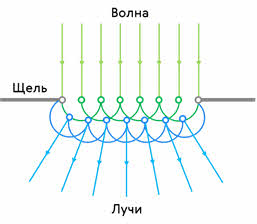
Явление дифракции, как и явление интерференции, присуще любому волновому процессу.

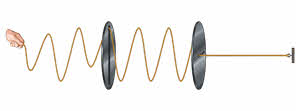
И рассмотрим ещё одно явление. Возьмём шнур, один конец которого прикрепим к стене. Возьмём верёвку, один конец которой закрепим к стене, и будем рукой создавать в ней колебания. Возбуждая колебания в шнуре мы видим, что колебания шнура происходят с разными амплитудами и в разных направлениях. Однако если его пропустить через узкую щель, то такая щель будет выделять из волны единственное направление колебаний, параллельное щели.

Теперь поставим на пути волны второй поляризатор с такой же щелью. Волна, выйдя из первой щели, свободно проходит через вторую, когда они параллельны. Если же повернуть вторую щель, перпендикулярно первой, то волна полностью гасится. Такую волну называют плоскополяризованной. То есть волна называется плоскополяризованной, если колебания во всех её точках происходят только в одной плоскости.

Прибор, превращающий неполяризованную волну в поляризованную, называют поляризатором. А прибор, позволяющий установить, поляризована или нет проходящая через него волна — анализатором.

Очевидно, что поляризация может происходить только в случае поперечных волн. Продольная волна не поляризуется.

Для закрепления материала решим с вами задачу. Разность хода двух когерентных волн с одинаковыми амплитудами равна 12 см, а длина волны — 8 см. Каков результат интерференции волн?