Раньше мы изучили метод последовательного конструирования алгоритмов, при котором алгоритм последовательно разбивается на подзадачи, пока все они не станут понятны исполнителю.
При конструировании алгоритмов вы уже наверняка сталкивались, с ситуацией, когда одна и та же последовательность действий выполнялась для различных данных в разных местах программы, то есть одну и ту же подзадачу решали несколько раз, так на пример в некоторых программах мы несколько раз выводили содержимое массива на экран. До этого, в таких случаях мы повторно записывали ту же последовательность команд, в результате чего наша программа становилась длиннее. А если вы допускали ошибки при написании программ, то наверняка заметили, что чем длиннее программа – тем сложнее в ней найти ошибку.
Но оказывается, что в таких случаях можно сократить текст программы, оформив соответствующие последовательности команд в виде вспомогательных алгоритмов, которые можно использовать многократно.
Вспомогательный алгоритм – это алгоритм, который целиком использован в составе другого алгоритма.
Ещё одной важной особенностью вспомогательных алгоритмов, является универсальность, то есть их можно использовать в совершенно разных программах, в которых они будут работать одинаково, то есть единожды написав, вспомогательный алгоритм вычисления площади треугольника, можно его использовать в любой, программе, в которой в ходе работы требуется вычислить площадь треугольника.
Задача: Робот находится в левой верхней клетке поля без стен. Нарисовать девять квадратов. Две на две клетки.
Очевидно, что при решении данной задачи мы будем повторять одну и ту же последовательность команд для рисования каждого квадрата. Следовательно, можно оформить её в качестве вспомогательного алгоритма, а также у нас есть три одинаковых ряда квадратов, последовательность команд для рисования которых можно так же оформить в виде вспомогательного алгоритма.
Для начала запишем последовательность команд для рисования квадрата в виде вспомогательного алгоритма, при этом условимся, что все квадраты будем рисовать, начиная с левой верхней клетки.
Для этого, строкой ниже основного алгоритма запишем служебное слово «алг» и название вспомогательного алгоритма, назовём его «квадрат», а затем ниже, служебные слова «нач» и «кон», между которыми и будут находится команды для рисования квадрата.

Вспомогательный алгоритм рисования квадрата
Так мы получили вспомогательный алгоритм для рисования квадрата. Теперь запишем вспомогательный алгоритм для рисования горизонтального ряда квадратов, назовём его ряд.
Чтобы нарисовать ряд квадратов, Робот должен нарисовать первый квадрат, для этого вызовем уже написанный алгоритм, записав его название. А затем нужно переместиться на позицию для рисования следующего квадрата. Для этого Робот должен трижды сместиться вправо, и один раз вверх. Далее нужно снова нарисовать квадрат и сместиться к следующему так же, как и до этого, трижды сместившись вправо и один раз вверх, и снова нарисовать квадрат.

Вспомогательный алгоритм рисования ряда квадратов
Теперь у нас есть алгоритм для рисования ряда квадратов. Запишем основной алгоритм. В нем нам можно сразу нарисовать ряд квадратов, вызвав соответствующий вспомогательный алгоритм. Теперь нужно переместиться на начальную позицию для рисования следующего ряда, для этого достаточно переместиться в левый ряд и на две клетки вниз. То есть записать цикл «пока слева свободно», содержащий команду «влево» и дважды команду «вниз». Теперь нам нужно снова нарисовать ряд квадратов и переместиться на начальную позицию, как мы делали до этого, записав цикл «пока слева свободно» с командой «влево» и дважды команду «вниз» и наконец, снова нарисовать ряд квадратов.

Основной алгоритм
Запустим программу на выполнение. Девять квадратов изображены верно, следовательно, задача решена.
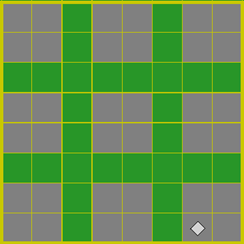
Результат работы программы
В блок-схеме вспомогательный алгоритм изображается как показано на рисунке. Этот блок называется «Предопределённый процесс», внутри него записывается название вспомогательного алгоритма, входные и выходные параметры.
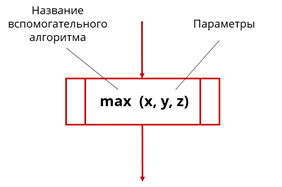
Изображение вспомогательного алгоритма на блок-схеме
Задача: У нас есть вспомогательный алгоритм factorial, который вычисляет значение факториала целого числа k. Составить блок-схему алгоритма вычисления значения выражения 1! + 2! + … + n!. Вспомним, что k! = 1 * 2 * … * k.
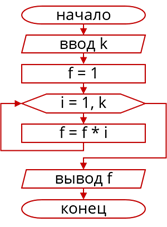
Блок-схема вспомогательного алгоритма
Изобразим блок-схему данного алгоритма. В ней через i обозначим порядковый номер слагаемого, для него же мы будем вычислять факториал. Через а обозначим значение итого слагаемого, а через r - значение данного выражения. В начале нам нужно считать значение числа n и присвоить r значение 0, т.к. оно ещё не включает ни одного слагаемого, затем будет идти цикл «Для i от 1 до n». В котором мы будем вычислять значение i-того слагаемого, используя вспомогательный алгоритм вычисления факториала, а затем увеличивать на это значение r. И в конце нам нужно вывести значение r.
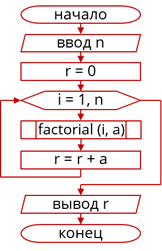
Блок-схема с использованием вспомогательного алгоритма
Рассмотрим, как работает вспомогательный алгоритм в составе основного. В начале выполняются команды основного алгоритма, идущие до вызова вспомогательного. Затем, когда доходит до выполнения вспомогательного алгоритма, его формальные параметры, в нашем случае k, заменяются параметрами из основного алгоритма. В нашем случае i. Далее выполняются команды вспомогательного алгоритма. Затем значения выходных параметров вспомогательного алгоритма, в нашем случае f подставляются в основной алгоритм, в нашем случае в переменную a. После чего далее выполняются команды основного алгоритма.
Через вспомогательные алгоритмы можно создавать так же рекурсивные алгоритмы. Рекурсивным алгоритмом называется алгоритм, который содержит ссылку на самого себя. Посмотрим для решения каких задач их можно применить.
Мы можем составить вспомогательный алгоритм для вычисления факториала, с использованием рекурсии, если примем во внимание формулу: n! = (n - 1)!. Важно при этом помнить, что 1! = 1. Блок-схема данного алгоритма будет выглядеть так.
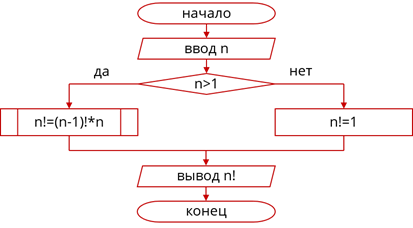
Блок-схема рекурсивного алгоритма вычисления n!
Обратим внимание, что вспомогательный алгоритм содержит ветвление, при котором, если n > 1 – n! = (n - 1)!, а в случае если n = 1, то n! = 1. Также и в других рекурсивных алгоритмах, ссылка на алгоритм всегда указывается лишь в одной ветви условного оператора, иначе он будет вызывать сам себя бесконечно.
Задача: Робот находится в поле без стен, на определённом расстоянии от левого края. Он должен нарисовать уголок, то есть закрасить все клетки от своего текущего положения до левого края, а потом столько же клеток вниз.
Запишем рекурсивный вспомогательный алгоритм для рисования уголка. Назовём его угол. Он будет содержать условный оператор, условием которого будет если слева свободно, если данное условие выполняется, робот будет закрашивать клетку, в которой он находится и смещаться на одну клетку влево, после чего снова вызывать себя. После условного оператора будут содержаться команды, которые будут выполняться, когда робот дойдёт до стены. На каждом шаге Робот должен закрасить клетку, в которой он находится и сместиться на клетку вниз.

Рекурсивный алгоритм рисования уголка
Основной алгоритм будет содержать только одну команду - вызов вспомогательного алгоритма угол. Запустим программу на выполнение. Робот действительно изобразил уголок.

Рассмотрим подробнее, как работает данный алгоритм. Для примера возьмём случай, когда робот стоит в трёх клетках от левого края поля. При первом вызове вспомогательного алгоритма условие выполняется, следовательно, робот закрасит клетку в которой находится и сместиться на клетку влево, после чего снова вызовет вспомогательный алгоритм для рисования уголка, уже во второй раз. При втором вызове вспомогательного алгоритма робот снова закрасит клетку, в которой находится, сместиться на клетку влево, и вызовет себя уже в третий раз. При третьем вызове слева будет край поля, следовательно, условие выполняться не будет, и выполнятся только команды, которые идут после условного оператора, то есть робот закрасит клетку, в которой находится и сместится на клетку вниз. При третьем вызове вспомогательный алгоритм был завершён окончательно, а при первых двух – нет, следовательно, сейчас будет продолжено выполнение второго вызова вспомогательного алгоритма, то есть Робот снова закрасит клетку, в которой находится и сместиться вниз. Второй вызов вспомогательного алгоритма завершён, осталось выполнить до конца лишь первый вызов алгоритма. При этом Робот снова закрасит клетку, в которой находится, и сместиться на клетку вниз. Уголок готов.
Выполнение рекурсивного алгоритма, для удобства можно представить в виде стека, то есть коробки, у которой есть дно, но нет верхней крышки, в такую коробку объект можно положить лишь поверх остальных, точно так же и достать из коробки можно лишь верхний объект. То есть объект, который в коробку положили первым, достанут из коробки последним. Так же происходит при выполнении вспомогательного алгоритма угол, в нашем примере, в процессе выполнения первого вызова алгоритма, он был вызван второй раз, а в процессе выполнения второго вызова, в третий. После того, как было завершено выполнение третьего вызова, было продолжено выполнение второго, а после его завершения – первого.
При использовании рекурсивных алгоритмов важно помнить, что количество одновременных вызовов ограничено, поэтому, если рекурсию можно заменить циклом – лучше так и поступить.
Важно запомнить:
· Вспомогательным называется алгоритм, который целиком используется в составе другого алгоритма.
· Рекурсивный алгоритм – это алгоритм, в котором есть ссылка на самого себя.
· Исполнение рекурсивного алгоритма можно представить в виде стека.
· Если рекурсию можно заменить циклом – лучше так и поступить.
Мы научились применять вспомогательные и рекурсивные алгоритмы при решении задач.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 15861
15861

