Вы знаете, ученик третьего класса Максим очень хотел объяснить вам эту тему, но немного приболел и прийти сегодня не смог. Но, благодаря Интернету, мы можем с ним связаться.
̶ Здравствуй Максим!

̶ Здравствуйте! Проверьте, чтобы ваши соседи по парте были готовы к уроку. И мы начинаем.
Прослушайте название пар множеств и попытайтесь заметить, что повторяется в каждой паре.
Животные и герои мультфильмов;
Рыбы и птицы;
Материки и части света;
Звёзды и планеты.
Ну, что заметили? Конечно, повторялся слово «и».
Если в названии множества есть союз «И», то каждый его элемент должен находиться на пересечении двух множеств, т.е. находиться одновременно в двух множествах. Другими словами мы можем сказать, что пересечение множеств – это их общая часть.
А теперь задание.
Необходимо разместить элементы по своим множествам.

Давайте посмотрим, что за элементы. Так это имена мальчиков и девочек: Коля, Ваня, Даша, Игорь, Катя, Саша, Дима, Юля, Ира, Женя. Будем размещать имена мальчиков в синий прямоугольник, а девочек – в розовый. Ага! Так ведь Сашей и Женей могут звать как мальчиков, так и девочек. Значит, эти два имени будут находиться сразу в двух множествах, т.е. на пересечении двух множеств.
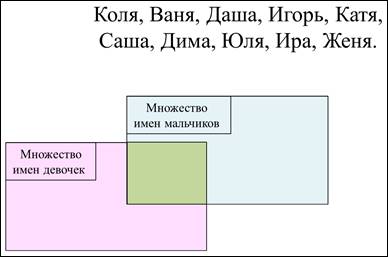
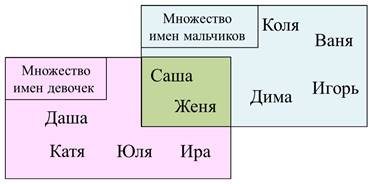
Итак, Коля, Ваня – это мальчики, помещаем эти элементы во множество имён мальчиков. Даша – имя девочки, помещаем в розовый прямоугольник, где находятся имена девочек. Игорь – имя мальчика, Катя – имя девочки. Саша, так могут звать и мальчика, и девочку, значит, этот элемент будет находиться на пересечении двух множеств. Дима – элемент из множества имён мальчиков. Юля, Ира, конечно элементы из множества имён девочек. И последнее имя, Женя, это имя могут иметь как девочки, так и мальчики. Значит, этот элемент будет находиться на пересечении двух множеств.
Теперь все имена находятся в своих множествах.
А сейчас я прочитаю названия ещё нескольких пар множеств, а вы попытайтесь заметить, что повторяется в этих парах.
Яблоки или груши;
Полевые или садовые цветы;
Попугаи или морские свинки;
Рабочие или выходные дни.
Заметили, что повторялось в парах множеств? Конечно, это слово «или».
Посмотрите ещё раз на названия множеств.
Например, яблоки или груши. А ведь эти множества можно объединить в одно с общим названием «фрукты» и все элементы будут располагаться в одном новом множестве.
Попугаи или морские свинки. Их можно объединить во множество с названием
«домашние животные» и все попугаи, и все морские свинки будут находиться в новом множестве.
Значит, если в названии множества есть слово «или», то его элемент может находиться в любом множестве и тогда происходит объединение множеств, т.е. эти множества объединяются.
Давайте рассмотрим два множества: домашние животные, дикие животные.
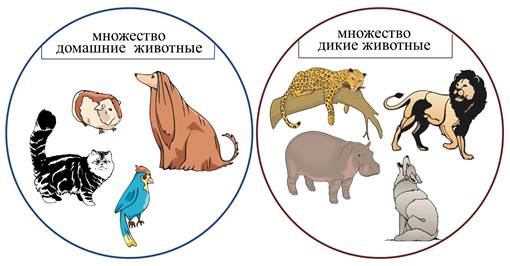
Множество домашние животные содержат следующие элементы: собака, кошка, морская свинка, попугай.
Множество дикие животные состоит из следующих элементов: бегемот, леопард, волк, лев.
Какой общий признак у элементов этих двух множеств? Элементы каждого из них относятся с животному миру. Значит, можно, объединив эти множества, создать новое множество под названием животные. Теперь все элементы находятся в одном множестве.

А теперь, конечно, задание.
Распределить элементы по множествам, объединить их и придумать название для нового множества.
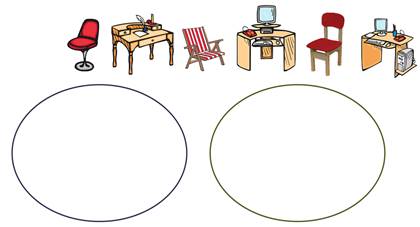
Итак, смотрим на элементы. Ага, у нас два множества: множество стульев и множество столов. Распределяем элементы по множествам. Все элементы стулья во множество стульев, а все элементы столы во множество столов.
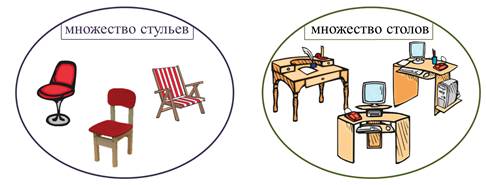
Объединяем множества. Какое название будет у нашего нового множества? Множество мебели.
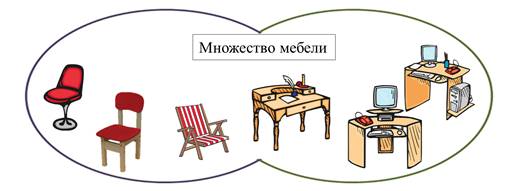
Давайте ещё раз определим разницу между пересечением и объединением множеств.
Если в названии множества есть слово «И», то это пересечение, и каждый элемент должен находиться на пересечении двух множеств.
Если в названии множества есть слово «или», то его элемент может находиться в любо области объединённых множеств.
Я надеюсь, что вы поняли разницу между пересечением и объединением множеств. А давайте проверим?
Итак, перед вами рисунок с тремя множествами.
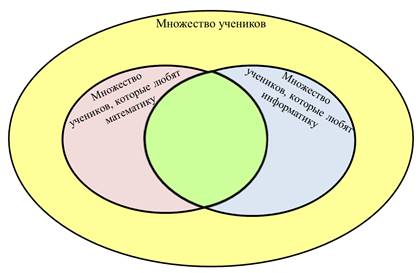
Множество учеников, которые любят математику, множество учеников, которые любят информатику и множество всех учеников. Но, среди учеников есть и такие, которые любят и математику и информатику. Значит, эти два множества пересекаются и одновременно они являются подмножеством множества всех учеников. А теперь появляются элементы во множествах.
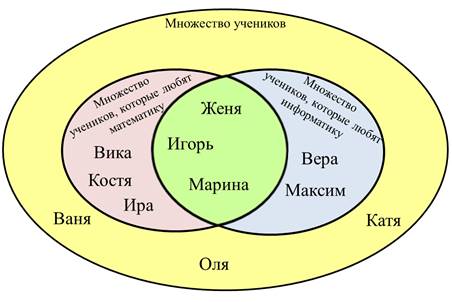
Используя полученные знания сегодня на уроке, будем отвечать на вопросы. А все ответы хранятся на этом рисунке, главное внимательно слушать вопросы и внимательно смотреть на рисунок.
Первый вопрос:
Сколько учеников любят математику? Считаем их во множестве учеников, которые любят математику, и не забываем посчитать тех учеников, которые находятся на пересечении двух множеств учеников, которые любят и математику, и информатику. Считаем. Их шесть.
Сколько учеников любят информатику? Считаем их во множестве учеников, которые любят информатику и опять считаем тех учеников, которые находятся на пересечении двух множеств. Считаем. Их пять.
Сколько учеников любят и математику, и информатику? Будем считать тех учеников, которые находятся на пересечении двух множеств. Их три.
Сколько учеников любят или математику или информатику? Если используется слово «или», значит элементы находятся в любом месте множеств за исключением любителей двух предметов сразу. Значит, считаем учеников и в первом множестве и во втором, но не включаем тех, кто находится в пересечении. Их пять.
Сколько учеников любят только математику? Любят математику только те, которые находятся во множестве учеников, которые любят математику. Ученики, которые находятся на пересечении двух множеств, сюда относится не будут, т.к. они любят и математику, и информатику. Итак, считаем и получается, что 3 ученика любят только математику.
Сколько учеников любят только информатику? Опять, учеников, которые находятся на пересечении двух множеств, считать не будем. Любителей информатики двое.
Сколько учеников не любят математику? Надо посчитать их во множестве учеников, которые любят информатику, кроме тех, которые находятся на пересечении множеств, т.к. эти ученики любят информатику и математику. А так же надо посчитать тех учеников, которые находятся во множестве всех учеников, т.к. они не любят математику. Их всего 5.
Всем спасибо за отличную работу. Теперь я точно понял, что хочу быть учителем!
Тебе спасибо, Максим. Тему объяснил хорошо. До свидания! А мы ещё сделаем выводы.
Итак.
Множество – это объединение некоторых объектов (элементов) в группу по определённым признакам.
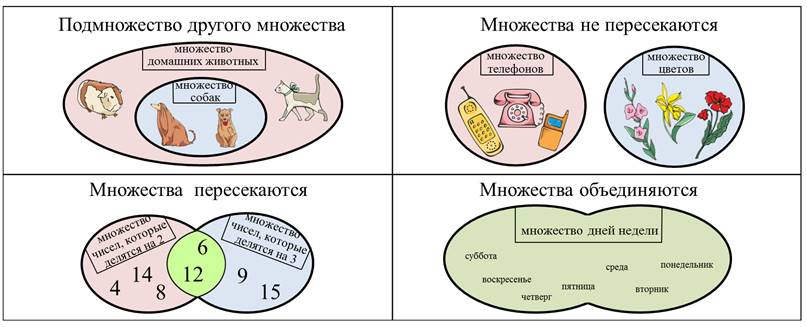
Множество может быть подмножеством другого множества. Например: множество собак является подмножеством множества домашние животные.
Множества могут пересекаться. Например: множество чисел, которые делятся на 2, и множество чисел, которые делятся на 3, пересекаются, т.к. числа, например, 6 и 12 делится и на 2, и на 3.
Множества могут и не пересекаться. Например: множество телефонов и множество цветов.
И множества могут объединяться. Например: множество рабочих дней недели и множество выходных можно объединить в одно множество дней недели.
Выводы сделаны, и я желаю вам успехов при выполнении заданий!

 Получите свидетельство
Получите свидетельство Вход
Вход



 5
5 13984
13984


Во втором классе достаточно базовых логических операций дизъюнкция, конъюнкция и инверсия. А исключающее или даже в 9 классе не дается, только в старших.
Здравствуйте, Надежда. При формулировании вопроса: «Сколько учеников любят математику или информатику?» ответ – 8. Здесь используется слово «или», значит элементы находятся в любом месте множеств. В вопросе же: «Сколько учеников любят ИЛИ математику, ИЛИ информатику?» ответ – 5. Данный вопрос на логику. Мы ищем учеников, которые любят или только математику, или только информатику. Ребята, расположенные на пересечении множеств, любят оба предмета сразу, а значит это не соответствует условию задания.
Но ведь здесь написано "или математику, или информатику". Это взаимоисключающие понятия. Подразумевается, что среди этих учащихся нет тех которые любят и математику, и информатику.
Здравствуйте, Надежда. Благодарим за сотрудничество. Обязательно проверим.
Исправьте ошибку
Сколько учеников любят или математику или информатику? Если используется слово «или», значит элементы находятся в любом месте множеств
за исключением любителей двух предметов сразу. Значит, считаем учеников и в первом множестве и во втором,но не включаем тех, кто находится в пересечении.Их восемь.