На одном из прошлых уроков мы с вами говорили о том, что всякое тело находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока на него не подействуют силы. То есть действие силы необходимо не для того, чтобы сохранить скорость тела постоянной, а чтобы изменить её. При этом действие силы может изменить как модуль скорости, так и её направление.
На экране вы видите шарик, закреплённый на столе с помощью резинового шнура. Если мы переместим шарик на некоторое расстояние, то шнур растянется и в нём возникнут силы упругости. Отпустим шарик. Под действием сил упругости он придёт в ускоренное движение и будет двигаться к своему первоначальному положению. При этом скорость шарика в любой точке траектории совпадает с направлением действующей на него силы, и, соответственно, с направлением вектора ускорения. Следовательно, при таком движении меняется только численное значение скорости, а направление её вектора остаётся неизменным, и шарик движется прямолинейно.
Повторим эксперимент. Но теперь мы не будем перемещать шарик, а толкнём его, придав некоторую начальную скорость, направленную перпендикулярно шнуру.
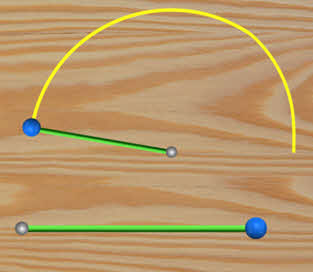
Если бы на шарик не действовали никакие силы, то, согласно закону инерции, он сохранял бы модуль и направление полученной скорости. Но, двигаясь, наш шарик удаляется от точки крепления шнура и слегка растягивает сам шнур. В результате в шнуре возникает сила упругости, пытающаяся вернуть его к первоначальной длине и одновременно с этим приблизить шарик к точке крепления шнура. Таким образом, в результате действия силы направление скорости шарика в каждый момент времени изменяется и шарик движется по криволинейной траектории. При этом в любой точке траектории, скорость направлена по касательной, а сила — к точке крепления шнура.
Рассмотренные примеры показывают, что действие на тело силы может привести к разным результатам в зависимости от направления векторов скорости и силы: если скорость тела и действующая на него сила направлены вдоль одной прямой, то тело движется прямолинейно, а если они направлены вдоль пересекающихся прямых, то тело движется криволинейно.
Криволинейное движение встречается гораздо чаще прямолинейного. С детства мы наблюдаем различные виды криволинейного движения, например, вращательное движение. Кто из нас не катался на карусели или не наблюдал за вращением волчка. Во вращательном движении участвуют и космические тела: планеты движутся вокруг Солнца, а спутники планет — вокруг планет.

Вообще, существует бесчисленное множество различных криволинейных траекторий. Однако любая кривая может быть представлена в виде совокупностей дуг окружностей разных радиусов. Поэтому чаще всего изучение криволинейного движения тела сводится к изучению его движения по окружности. Мы будем изучать самый простой вид такого движения — движение тела по окружности с постоянной по модулю скоростью. Таким телом, вращающимся с постоянной скоростью вокруг неподвижной оси, могут быть точильный круг, колесо автомобиля, винт самолёта и так далее.
Мгновенная скорость движения тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. В этом можно убедиться, если прижать к вращающемуся точильному камню конец детали.
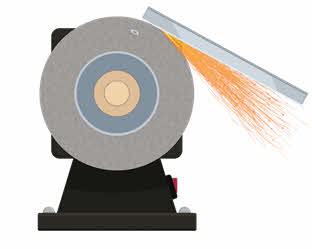
Теперь рассмотрим материальную точку, движущуюся по окружности радиусом R. Будем задавать положение этой точки с помощью радиус-вектора, проведённого из центра окружности к материальной точке.
При движении точки по окружности её радиус-вектор непрерывно поворачивается — совершает вращательное движение. Например, если за время Δt движущаяся точка переместится по окружности из точки А в точку B, то за это время её радиус-вектор повернётся на угол Δφ, который называют углом поворота.
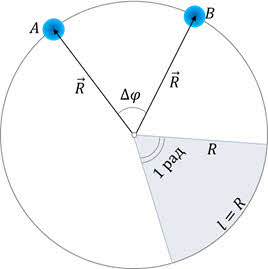
В СИ угол поворота измеряется в радианах.
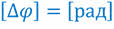
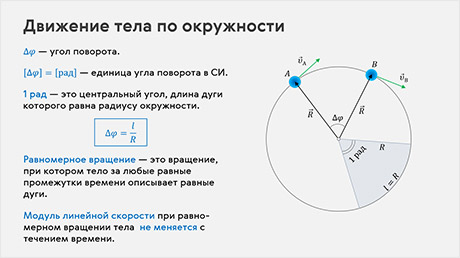
Угол в один радиан — это центральный угол, длина дуги которого равна радиусу окружности. Значение любого угла в радианах равно отношению длины дуги к радиусу окружности.
Давайте посмотрим на стробоскопическую фотографию движения тела по окружности. На ней хорошо видно, что вращающееся тело за равные промежутки времени описывает равные дуги, (или поворачивается на одинаковый угол).
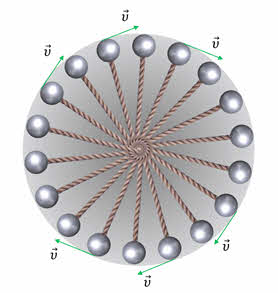
Следовательно, при таком движении модуль мгновенной скорости тела не меняется с течением времени. Такое вращение называется равномерным. Но будьте внимательны. При равномерном вращение не меняется только модуль скорости, но меняется её направление от точки к точке, то есть ускорение тела не равно нулю. В случае движения тела по окружности мгновенную скорость мы будем называть линейной скоростью тела.
Быстроту вращательного движения характеризуют угловой скоростью. Её обозначают буквой ω. При равномерном вращении угловая скорость определяется, как величина, численно равная углу поворота радиус-вектора за единицу времени:
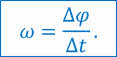
Единицей угловой скорости в СИ является радиан в секунду.
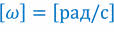
Движение, при котором тело движется по окружности с постоянной угловой скоростью, называют равномерным движением по окружности.
— А связаны ли между собой линейная и угловая скорости?
Чтобы ответить на этот вопрос, давайте подставим выражение для угла поворота в формулу для угловой скорости:

Также для характеристики вращательного движения вводятся специальные величины — частота и период обращения.
Частотой обращения называется величина, численно равная числу оборотов, совершаемых телом за единицу времени:
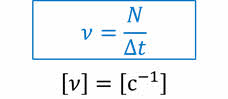
Периодом обращения называется промежуток времени, в течение которого тело совершает один полный оборот по окружности.
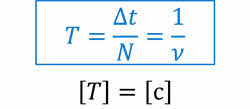
Сравнивая формулы для расчёта частоты и периода обращения, можно заметить, что они взаимно обратные.
Угловая скорость, периода и частота обращения связаны между собой формулами:

Ранее мы с вами упомянули, что при равномерном вращении тела по окружности модуль линейной скорости не меняется, но меняется её направление. То есть движение по окружности всегда происходит с ускорением. Конечно у вас может возникнуть вопрос: как определить модуль и направление этого ускорения?
Итак, пусть материальная точка, двигаясь по окружности с постоянной по модулю скоростью, за некоторый промежуток времени перемещается из положения А в положение В. Скорость материальной точки в этих положениях направлена по касательной к окружности в этих точках.
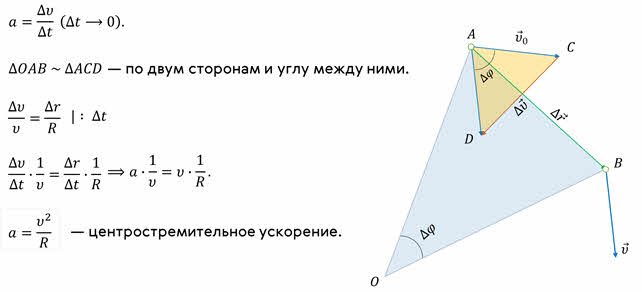
Полученная формула определяет модуль ускорения при равномерном движении тела по окружности.
— А как направлено это ускорение?
Его направление совпадает с тем направлением, которое примет вектор изменения скорости, при Δt → 0 . Из рисунка видно, что чем меньше угол поворота, тем ближе направление вектора изменения скорости к направлению на центр окружности. Значит, ускорение направлено по радиусу к центру окружности. По этой причине его называют центростремительным.
Согласно второму закону Ньютона, ускорение всегда сонаправлено с силой, в результате действия которой оно возникает. Это справедливо и для центростремительного ускорения. Поэтому, сила, под действием которой тело движется по окружности с постоянной по модулю скоростью, в каждой точке направлена по радиусу окружности к её центру.
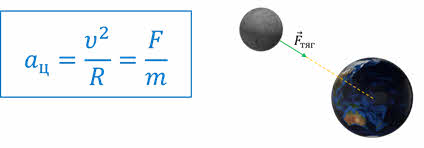
Закрепления материала.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 11800
11800

