Равномерное движение точки по окружности

Движение тела по окружности довольно часто встречается в повседневной жизни. Взять хотя бы движение Земли вокруг своей оси или вокруг Солнца.

Кроме этого существуют ещё сотни примеров: вращение колеса автомобиля, вращение электронов вокруг ядра атома, движение стрелок часов и многое другое.

В первую очередь, давайте условимся, что называется равномерным движением по окружности? При прямолинейном движении мы говорили о том, что тело совершает одинаковые перемещения за равные промежутки времени. В случае с движением тела по окружности, равномерным движением называется такое движение, при котором тело поворачивается на одинаковые углы за равные промежутки времени.

Мы уже говорили о том, что мгновенная скорость направлена по касательной к траектории движения. Значит, при движении тела по окружности, его скорость будет направлена по касательной к этой окружности в данной точке. При этом, модуль скорости, так же, как и модуль ускорения остаётся постоянным, в то время как их направления постоянно меняются.

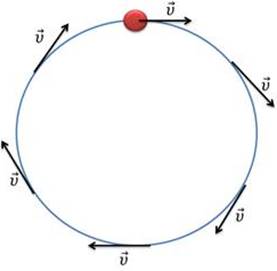
Из этого можно сделать вывод, что любое криволинейное движение является ускоренным, даже если модуль скорости остаётся постоянным.

Давайте рассмотрим ускорение при движении тела по кривой. Поскольку направление ускорения постоянно меняется, имеет смысл рассматривать мгновенное ускорение. Точно так же, как и в случае с мгновенной скоростью, мы будем брать все меньшие и меньшие промежутки времени.

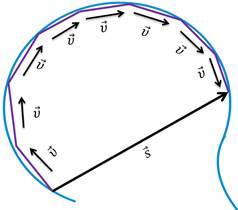
Тогда, можем записать, что мгновенное ускорение — отношение изменения скорости к промежутку времени, за который это изменение произошло, при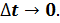  

Возьмём две произвольные точки А и В, принадлежащие окружности. В обеих точках скорость будет направлена по касательной, а модуль скорости в точке A будет равен модулю скорости в точке B.

Воспользуемся теперь сложением скоростей, чтобы найти вектор показывающий направление изменения скорости. Рассмотрим два треугольника, показанные на рисунке. Один из этих треугольников образован двумя радиусами и вектором перемещения, а второй — двумя модулями скорости и вектором изменения скорости. Эти треугольники подобны, т.к. являются равнобедренными и имеют одинаковый угол при вершине. Напомним, что мы рассматриваем промежуток времени, стремящийся к нулю. В этом случае, угол поворота будет стремиться к нулю, а значит и угол между скоростью в точке A и скоростью в точке B — тоже будет стремиться к нулю.

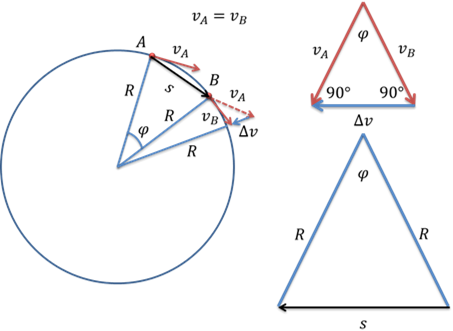
Поскольку сумма углов треугольника равна 180^o, и в равнобедренном треугольнике углы при основании равны, мы можем сделать вывод, что угол между вектором скорости и вектором изменения скорости составляет 90^o. Это очень важный вывод, т.к. вектор изменения скорости указывает направление ускорения. Поскольку радиус всегда перпендикулярен касательной, ускорение направлено по радиусу, то есть, стремиться к центру. Именно поэтому, ускорение при криволинейном движении называется центростремительным.

Теперь разберёмся с модулем ускорения. Мы снова используем те же два треугольника. Поскольку треугольники подобны, мы можем записать, что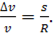  

Перемещение мы можем записать как произведение скорости и времени: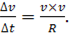

Теперь преобразуем выражение: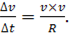

Это, как раз, и будет модулем ускорения:

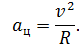
Таким образом, мы выяснили, что ускорение при движении по окружности направлено к центру и численно равно отношению квадрата скорости к радиусу окружности.

В завершении темы, вспомним несколько важных физических величин, описывающих криволинейное движение. В первую очередь, это, конечно, период обращения. Периодом обращения называется время, за которое тело совершает полный оборот.

Например, период обращения Земли вокруг Солнца равен одному году.

Существует также величина, обратная периоду, которая называется частотой. Эта величина равна числу оборотов в единицу времени. Очевидно, что период обращения и частота обратно пропорциональны:

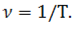
К примеру, чем быстрее вращаются лопасти вентилятора, тем больше он оборотов совершит в единицу времени и тем меньше период обращения.

Еще одной важной характеристикой движения по окружности является угловая скорость. Скорость, о которой мы говорили до этого — это фактическая скорость движения, которая называется линейной.

Угловая скорость характеризует скорость поворота, то есть изменение угла поворота в единицу времени.

Таким образом, угловая скорость измеряется в радианах в секунду:

.

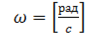Напомним, что радиан — это угол между двумя радиусами окружности, вырезающими на окружности дугу, длина которой равна радиусу окружности. Применительно к физике, мы можем сказать, что радиан — это такой угол, при повороте на который, точка проходит путь, равный радиусу окружности.

Мы знаем, что полный оборот — это поворот на угол, равный 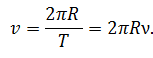. Тогда, угловая скорость будет равна:

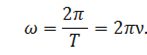
Линейная скорость будет определяться:

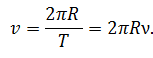
Также можно записать, что линейная скорость равна произведению угловой скорости и радиуса окружности:

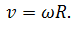
Это вполне логично: чем дальше точка находится от центра, вокруг которого она вращается, тем больше должна быть её линейная скорость, чтобы за одинаковое время совершить поворот на одинаковый угол.

Мы рассмотрели частный случай: когда точка совершает полный оборот по окружности. В более общем случае, угловая скорость будет определяться как отношение угла поворота ко времени, за который этот поворот был совершён:

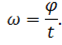
 Аналогично, линейная скорость определяется как отношение длины пройденной дуги ко времени:

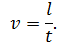
Для примера рассмотрим, так называемый, геостационарный спутник. Это искусственный спутник Земли, который постоянно находится над одной и той же точкой поверхности Земли (с помощью таких спутников работает спутниковое телевидение, к примеру). Для выполнения этого условия необходимо, чтобы спутник вращался с той же угловой скоростью, что и Земля.

Пример решения задачи.

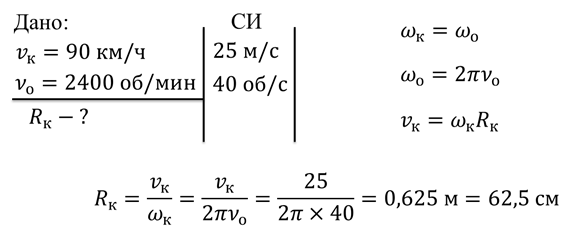
Задача. Спидометр автомобиля показывает 90 км/ч, а тахометр — 2400 об/мин. Чему равен радиус колеса в таком случае?