Определение:
Зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение y, называют функцией.
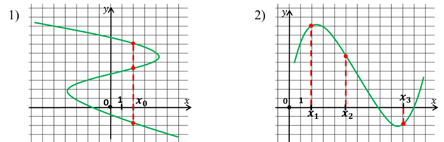
В определении сказано, что только та зависимость является функцией, у которой каждому значению аргумента соответствует единственное значение функции.
Рассмотрим первый график. Видим, что одному значению x может соответствовать несколько значений y. Значит, данная зависимость не является функцией.
Обратимся ко второму случаю. Какие бы значения аргумента мы не брали, каждому из них соответствует только одно значение функции. Можно сказать, что эта зависимость является функцией.
В общем виде любую функцию можно записать так:
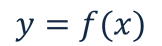
Например:
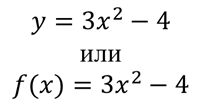
Понятно, что функция может принимать различные значения в зависимости от значения аргумента. Найдём значение каждой функции при заданном значении аргумента.
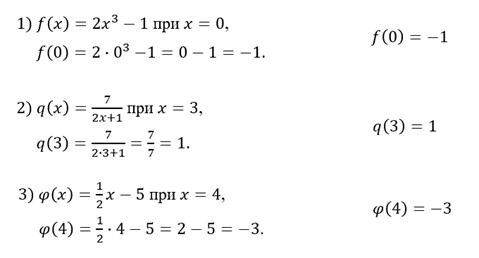
Вы заметили, что в этом задании функции названы разными буквами. Действительно, функцию можно называть любой буквой латинского алфавита.
Ранее вами были изучены несколько важных функций. Вспомним их.
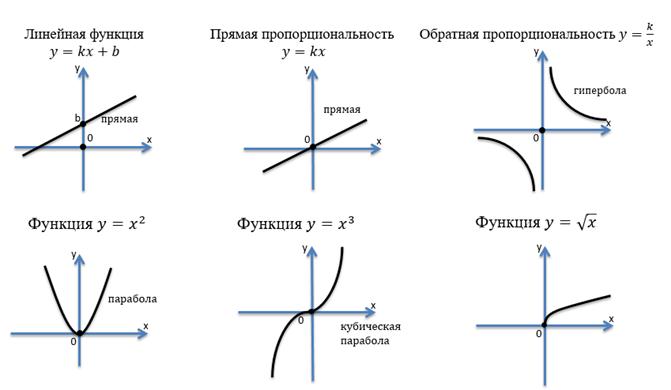
Сейчас попробуем выяснить, как же получается график функции, и дадим определение этому понятию.
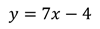
Можно записать её в таком виде:
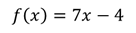
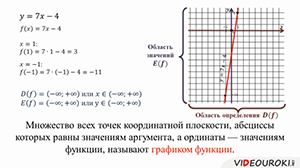
Это линейная функция, графиком как вы помните, является прямая. Для изображения прямой достаточно двух точек.
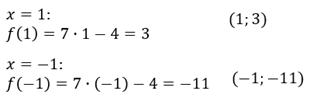
Получаем точки с координатами (1;3) и (-1;-11).
Проведём прямую через полученные точки.
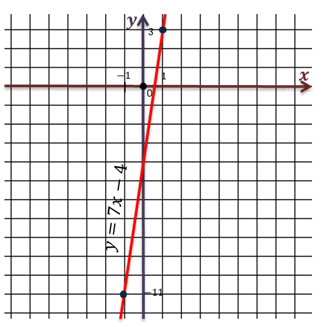
Мы изобразили график функции.
Определение:
Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — значениям функции, называют графиком функции.
Все значения аргумента, т.е. переменной x образуют область определения функции, а все значения зависимой переменной, т.е. y, — область значений функции.
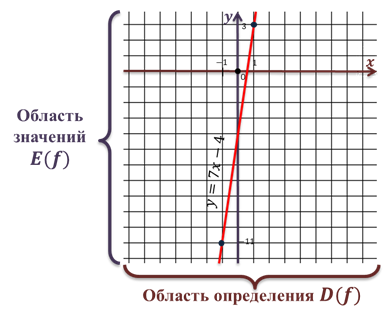
В данном случае x и y могут быть любыми числами, т.е. областью определения и областью значений является множество всех действительных чисел.
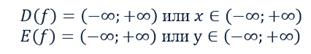
Потренируемся находить область определения и область значений функции по её графику.
Область определения можно находить не только по графику функции, но и по формуле, с помощью которой задана функция.
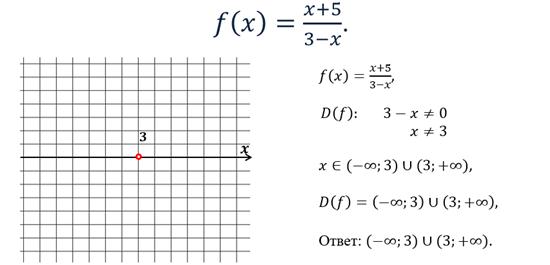

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 45385
45385

