Правильно. Это все предметы, люди вокруг нас и всё, что с ними происходит. А как вы думаете, почему окружающие нас строения, памятники, машины и так далее иногда называют объектами, иногда — предметами?..
Оказывается, любой объект может стать предметом. Для этого человеку надо проявить к объекту интерес, например: проанализировать его форму, изучить конструкцию, определить его назначение, размеры и прочее. В этом случае объект становится предметом изучения. А при изображении объекта, например на листе в тетради, он становится предметом изображения. На уроках черчения вы будете работать с реальными предметами, моделями, с наглядными изображениями деталей машин и изделий. В стандартах ЕСКД установлены следующие определения этих понятий.
Изделие — это любой предмет или набор предметов, изготовленный на предприятии (например, болт и гайка, холодильник и самолёт).
Деталь — это изделие, изготовленное из однородного материала без применения сборочных операций (например, швейная игла, ложка с вилкой, зубчатое колесо).
А модель — это предмет, воспроизводящий в натуральную величину или в масштабе какое-либо изделие.
Модели геометрических тел, деталей могут быть выполнены из бумаги, картона, дерева, пластилина и других материалов. Кроме того, чертёж, эскиз, технический рисунок также являются моделями, так как представляют собой графическое изображение изделия.
Вы уже знаете, что основным элементом технической графики являются линии. Определённое сочетание линий образует на плоскости геометрические фигуры. Знание особенностей и названий линий и геометрических фигур необходимо всем, изучающим черчение.
Линии классифицируют: по характеру, по положению в пространстве, по взаимному положению и по ограничению.
По характеру линии делятся на: прямые, кривые и ломаные.
По положению в пространстве линии бывают горизонтальные, вертикальные и наклонные.
По взаимному положению: параллельные и пересекающиеся.
А по ограничению линии делятся на отрезки и лучи.

Замкнутые кривые и ломаные линии образуют геометрические фигуры. Их вы знаете по урокам изобразительного искусства, математики и технологии. Чтобы правильно читать и выполнять чертежи, надо запомнить определение каждой геометрической фигуры.
Круг — это часть плоскости, ограниченная окружностью.
Сегмент — часть круга, ограниченная дугой окружности и её хордой.
Сектор — часть круга, расположенная между двумя радиусами круга и дугой окружности, ограниченной этими радиусами.
Кольцо — часть плоскости, заключённая между двумя окружностями, проведёнными из одного центра.
Соответственно, полукольцо — это часть плоскости, заключённая между двумя полуокружностями, проведёнными из одного центра.

Многоугольник — это часть плоскости, ограниченная замкнутой ломаной линией. Многоугольники, у которых все стороны и углы равны, называют правильными. Остальные многоугольники являются неправильными.
Треугольник — это многоугольник, имеющий три стороны, три угла и три вершины. Если все стороны и углы треугольника равны между собой, то такой треугольник является правильным.
Четырёхугольник — это многоугольник, имеющий четыре стороны и четыре угла. Правильным четырёхугольником является квадрат.
Квадрат — это четырёхугольник, у которого все стороны равны и все углы прямые.
Если у четырёхугольника равны и параллельны только противоположные стороны, а все углы прямые, то такой четырёхугольник называется, правильно, прямоугольником.

Каждая геометрическая фигура представляет собой сочетание определённых элементов, которые надо знать.

Все рассмотренные нами геометрические фигуры являются плоскими, то есть имеющими два измерения. Поэтому геометрическую фигуру нельзя взять в руки. Любая геометрическая фигура всегда является двумерным изображением или элементом объёмной фигуры.
В отличие от плоских фигур объёмные геометрические фигуры, или тела, имеют три измерения — длину, высоту, ширину — и являются частью трёхмерного пространства. Объёмные геометрические фигуры всегда можно взять в руки.
Геометрическое тело (или фигура) — это замкнутая часть пространства, ограниченная поверхностями. К геометрическим телам относят многогранники и тела вращения.
Многогранники — это геометрические тела, ограниченные со всех сторон многоугольниками. К ним относят призмы и пирамиды.
Тела вращения — геометрические тела, образованные вращением плоской геометрической фигуры или её части вокруг оси. К ним относят цилиндры, конусы, шары и торы.
А теперь посмотрите на эти призмы. Что у них общего?.. Верно: у каждой призмы два одинаковых основания, являющихся многоугольниками (четырёхугольники, треугольники, шестиугольники), а боковые грани — всегда четырёхугольники. Это характерные особенности призм. На основании характерных признаков можно сформулировать определение призмы.

Призма — это многогранник, имеющий два основания — равные и параллельные многоугольники и боковые грани — четырёхугольники.
Призму называют правильной, если в её основании лежит правильный многоугольник, и неправильной, если в её основании — неправильный многоугольник.
Призму называют прямой, если её боковые грани перпендикулярны основаниям, и наклонной, если боковые грани не перпендикулярны основаниям.
Полная характеристика призмы должна звучать примерно так: правильная прямая четырёхугольная призма; неправильная прямая четырёхугольная призма; неправильная наклонная четырёхугольная призма.

К призмам относят куб и прямоугольный параллелепипед, так как эти многогранники соответствуют определению призм.
Куб (гексаэдр) — это многогранник, ограниченный шестью квадратами. Или можно сказать, что это правильная прямая четырёхугольная призма, у которой боковые грани — квадраты.
Прямоугольный параллелепипед — это многогранник, у которого все грани — прямоугольники, которые попарно равны и параллельны. Или же это неправильная прямая четырёхугольная призма, в основании которой — прямоугольник.
Теперь давайте посмотрим на изображение пирамид и установим их характерные существенные признаки. Очевидно: у пирамид одно основание, являющееся многоугольником (треугольником, шестиугольником и так далее); боковые грани — треугольники, имеющие общую вершину.

Таким образом, пирамида — это многогранник, у которого основание — многоугольник, а боковые грани — треугольники, имеющие общую вершину (называемую вершиной пирамиды).
Пирамиды бывают правильными и неправильными, полными и усечёнными. Особенность усечённых пирамид — это наличие у них двух подобных оснований.

Характеристика пирамиды должна звучать, например, так: правильная треугольная пирамида, правильная шестиугольная пирамида и так далее.
А теперь посмотрите на изображение прямых цилиндров. Подумайте, как образуется цилиндрическая поверхность. Догадались? Да, путём вращения прямоугольника вокруг одной из его сторон.

Ещё раз внимательно посмотрите на наши цилиндры и попробуйте самостоятельно установить их признаки.
Наверняка вы думаете правильно, что у цилиндра два существенных и два несущественных признака. Существенные признаки это:
· Наличие двух оснований — двух параллельных кругов одинакового диаметра.
· И наличие боковой цилиндрической поверхности.
А несущественные признаки — это величина радиуса основания и высота цилиндра. Зная существенные и несущественные признаки цилиндра, можно сформулировать определение прямого цилиндра.
Прямой круговой цилиндр — это геометрическое тело, образованное вращением прямоугольника вокруг оси, совмещённой с одной из его сторон. У прямого цилиндра два одинаковых параллельных основания — круги, а боковая поверхность — цилиндрическая.
Теперь посмотрим на конус. Как вы думаете, как образована эта коническая поверхность? Верно, вращением прямоугольного треугольника вокруг одного из его катетов.

У конуса есть два существенных признака: наличие одного основания, имеющего форму круга, и боковой конической поверхности, имеющей вершину.
Таким образом, прямой круговой конус — это геометрическое тело, образованное вращением прямоугольного треугольника вокруг оси, совмещённой с одним из его катетов. У него основание — круг и боковая коническая поверхность.
Конус может быть полным и усечённым. Попробуйте самостоятельно сформулировать определение усечённого прямого конуса. А теперь сравните свой ответ с нашим: усечённый конус — геометрическое тело, образованное вращением прямоугольной трапеции вокруг меньшей боковой стороны.

Если мы с вами будем вращать круг вокруг одной из его осей, то мы с вами получим ещё одно геометрическое тело — шар. Шар со всех сторон виден как круг.
А каковы несущественные признаки шара?.. Верно, величина его диаметра.

А как вы думаете, какое геометрическое тело можно получить, если вращать круг вокруг оси, лежащей в плоскости круга, но не проходящей через его центр?..
Действительно, — это тор. Подумайте, какие известные вам предметы напоминают изображения тора? Верно, первое изображение напоминает баранку или спасательный круг. Второе яблоко, а третье — лимон, ну или бочку.

Запомните. Когда круг вращается вокруг оси, расположенной за его пределами, тор имеет форму, условно называемую «кольцо». При вращении большей части круга вокруг его хорды как вокруг оси образуется тор «яблоко». При вращении меньшей части круга вокруг его хорды образуется тор «лимон».
Геометрические тела состоят из сочетания элементов: оснований; боковых поверхностей; боковых граней, имеющих рёбра; образующих; вершин. Знание этих элементов необходимо при изучении черчения. На экране изображены геометрические тела, показаны и названы все эти элементы. Рассмотрите каждое геометрическое тело на этих рисунках и запомните названия их элементов.

 Получите свидетельство
Получите свидетельство Вход
Вход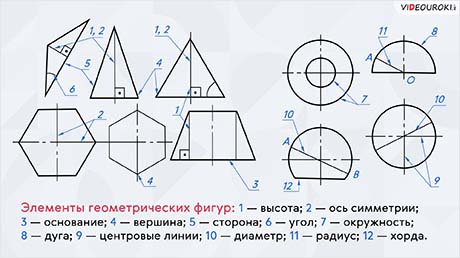




 1004
1004

