Тест на повторение по темам ЕГЭ 12-17 от 17.02.22

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.

1. заменить (v, w) 
2. нашлось (v)

Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Дана программа для исполнителя Редактор:

НАЧАЛО
ПОКА нашлось (9999) ИЛИ нашлось (333)
  ЕСЛИ нашлось (9999)
    ТО заменить (9999, 3)
    ИНАЧЕ заменить (333, 99)
  КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ

Какая строка получится в результате применения приведённой выше программы к строке, состоящей из 194 идущих подряд цифр 3? В ответе запишите полученную строку.

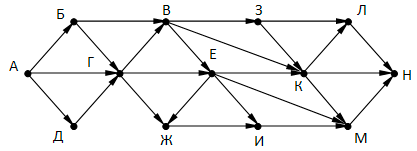
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. В ответе укажите последний в лексикографическом (алфавитном) порядке маршрут из города А в город Н, не проходящий через город Е и содержащий ровно восемь городов, включая города А и Н; города в маршруте указывайте заглавными буквами без разделителей.

Значение арифметического выражения: 9²⁰ + 3⁶⁰ – 25 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?

На числовой прямой даны три отрезка: P = [5, 100], Q = [15, 25] и R = [35,50]. Какова наименьшая длина отрезка A, при котором формула

((x ∈ P) → (x ∈ Q)) ∨ (¬(x ∈ A) → ¬(x ∈ R))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х?

Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями:

F(n) = n + 3, при n ≤ 3
F(n) = F(n – 2) + n, при n > 3 и четном значении F(n-1),
F(n) = F(n – 2) + 2•n, при n > 3 и нечетном значении F(n-1).

Определите сумму значений, являющихся результатом вызова функции для значений n в диапазоне [40; 50].

В файле 17-205.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар, в которых хотя бы один из двух элементов заканчивается на 17, а их сумма делится на 2. В ответе запишите два числа: сначала количество найденных пар, а затем – максимальную сумму элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности (в ответе записать два числа, разделенных одним пробелом)