Создать тест
ВходВариант 2. Системы и совокупности квадратных неравенств
Список вопросов теста
Вопрос 1
Какое число является решением системы неравенств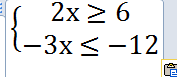 
Варианты ответов
-
\(-3\)
-
\(-4\)
-
\(5\)
-
\(2\)
Вопрос 2
Решите систему неравенств 
Варианты ответов
-
\(1<х<6\)
-
\(6\leх\le5\)
-
\(1\leх\le6\)
-
нет решений
Вопрос 3
Укажите систему неравенств, решения которой отмечены штриховкой на координатной прямой
____________2_!_!_!_!_!_!_!_!_!_!_!
Варианты ответов
Вопрос 4
Какое неравенство не имеет решения?
Варианты ответов
-
\(|х|>-3\)
-
\(|х|\le0\)
-
\(|х|<-6\)
-
\(|х|-2<7\)
Вопрос 5
Какому из условий равносильно неравенство \(\left|х\right|\le7\)
Варианты ответов
-
\(-7\leх\le7\)
-
\(х\le\ -7\ или\ \ х\ge7\)
-
\(х\le7\)
-
\(-7<х<7\)
Вопрос 6
Выберите верное утверждение
Варианты ответов
-
\(если\ а\ >-6,\ то\ |а|<6\)
-
\(если\ а>-6,\ то\ |а|>6\)
-
\(если\ а<-6,\ то\ |а|>6\)
-
\(если\ а<-6,\ то|а|<6\)
Вопрос 7
Решите неравенство \(-2<5х+3\le13\)
Варианты ответов
-
\(-1<х<2\)\(\)
-
\(-1<х\le2\)\(\)
-
\(\frac{1}{5}<х\le3\frac{1}{5}\)\(\)
-
\(-\frac{1}{4}<х\le1\frac{5}{8}\)
Вопрос 8
Найти наименьшее целое положительное решение неравенства \(\frac{9х-3}{5х+20}>0\)
Варианты ответов
-
\(-8\)
-
\(-6\)
-
\(-5\)
-
\(-4\)
Вопрос 9
При каких значениях b корень уравнения
\(x-4=b\) является отрицательным числом?
Варианты ответов
-
\(b\ge-4\)
-
\(b<-4\)
-
\(b\le-4\)
-
\(-4<b\le0\)
Вопрос 10
Решите систему 
Варианты ответов
-
\(x\ge-6\)\(\)
-
\(x\le-2\)\(\)
-
\(-6\le x\le-2\)\(\)
-
\(-2<x<6\)
Получите комплекты видеоуроков + онлайн версии
0
306
Нравится
0
