Решение неравенств методом интервалов

Мочалова Елена Вячеславовна

23.04.2020. Тест. Алгебра, 11 класс

Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного использования. Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.

Решение неравенств методом интервалов, подготовка к экзамену

Система оценки: 5 балльная

Список вопросов теста

Вопрос 1

Решение какого из данных неравенств изображено на рисунке?

Варианты ответов

x^2-4<0
x^2+4<0
x^2-4>0
x^2+4>0

Вопрос 2

На каком рисунке изображено множество решений неравенства \(\left(2x-5\right)\left(x+3\right)\ge0\)

Вопрос 3

Решите неравенство \(\frac{x-2}{3-x}\ge0\)

На каком рисунке изображено его решение?

Вопрос 4

Найдите область определения функции \(y=\log_6\left(25-x^2\right).\)

Варианты ответов

[-5;5]
{-5;5)
(-00; -5]U[5;+00)
(-00; -5)U([5;+00)

Вопрос 5

Укажите порядок действий при решении неравенства методом интервалов.

Варианты ответов

Перенести все слагаемые в левую часть неравенства и разложить её на множители.
Рассмотреть соответствующую функцию и найти её нули.
Изобразить нули функции на числовой прямой.
На каждом промежутке, полученном в результате разбиения области определения нулями функции, определить знак функции.
Записать ответ.

Вопрос 6

Сколько нулей имеет функция F(x), если известно, что они разбивают непрерывную область определения на 9 промежутков?

Варианты ответов

Вопрос 7

Используя график функции y=F(x), укажите промежутки, являющиеся решением неравенства F(x)>0.

Варианты ответов

(-00; 2)
(-2;0)
(0;3)
(3;7)
(7;+00)

Вопрос 8

Укажите целое число, которое является решением неравенства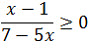

Вопрос 9

Решите неравенство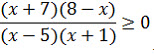

Варианты ответов

(-7;-1)U(5;8)
[-7;-1]U[5;8]
[-7;-1)U(5;8]
(-7;-1]U[5;8)

Вопрос 10

При расстановке знаков удобно пользоваться следующим правилом:

• если линейный множитель x-x₀ стоит в нечётной степени, то при переходе через точку x₀ знак ……;

• если линейный множитель x - x₀ стоит в чётной степени, то при переходе через точку x₀ знак …..

Укажите пропущенные слова через один пробел.