Проверочный тест по темам ЕГЭ 12-18 от 14.03.22
Список вопросов теста
Вопрос 1
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.
1. заменить (v, w) 2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (63) ИЛИ нашлось (664) ИЛИ нашлось (6665)
ЕСЛИ нашлось (63) ТО заменить (63, 4)
ИНАЧЕ
ЕСЛИ нашлось (664) ТО заменить (664, 65)
ИНАЧЕ
ЕСЛИ нашлось (6665) ТО заменить (6665, 63) КОНЕЦ ЕСЛИ
КОНЕЦ ЕСЛИ
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой выше программы к строке, в которой первая и последняя цифры – 3, а между ними стоит 115 цифр 6? В ответе запишите полученную строку.
Вопрос 2
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Какова длина самого длинного пути из города А в город Ж? Длиной пути считать количество дорог, составляющих этот путь.
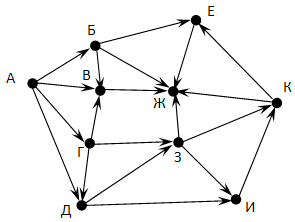
Вопрос 3
Значение арифметического выражения: 97 + 38 – 5 записали в системе счисления с основанием 3. Какая из цифр реже всего встречается в полученном числе? В ответе укажите, сколько таких цифр в этой записи.
Вопрос 4
Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наибольшее натуральное число A, такое что выражение
(X & A ≠ 0) → ((X & 20 = 0) → (X & 5 ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Вопрос 5
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 2·n при n < 3 F(n) = 3·n + 5 + F(n–2), если n ≥ 3 и чётно, F(n) = n + 2·F(n–6), если n ≥ 3 и нечётно.
Чему равно значение функции F(61)?
Вопрос 6
В файле 17-4.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от 0 до 10 000 включительно. Рассматривается множество элементов последовательности, которые оканчиваются на 5 или 7 и при этом не делятся ни на 9, ни на 11. Найдите количество таких чисел и сумму минимального и максимального из них.
Вопрос 7
Квадрат разлинован на N×N клеток (2 < N < 20). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх – в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается, при столкновении со стеной робот разрушается. В каждой клетке записано число – количество монет, которое необходимо заплатить за проход. Если число отрицательное – счёт робота уменьшается, если положительное – увеличивается. Начальным значением счёта является значение стартовой клетки. Определите максимальное значение счета робота при движении из левой нижней клетки поля в правую верхнюю, если:
А) роботу запрещено перемещаться при отрицательном счёте,
Б) робот может перемещаться при отрицательном счёте.
Исходные данные для Робота записаны в файле 18-117.xls в виде прямоугольной таблицы, каждая ячейка которой соответствует клетке квадрата. В ответе запишите сначала ответ на вопрос А, затем – ответ на вопрос B.
Получите комплекты видеоуроков + онлайн версии
 0
0 629
629 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








