Проверочный тест на повторение_1 вариант

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
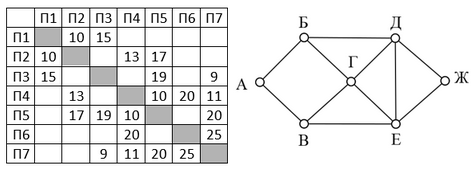Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. В таблице в левом столбце указаны номера пунктов, откуда совершается движение, в первой строке – куда. Определите длину дороги между пунктами А и Б, если известно, что длина дороги между Г и Д меньше длины дороги между Г и Е. Передвигаться можно только по указанным дорогам.

Для кодирования некоторой последовательности, состоящей из букв П, О, Е, Х, А, Л, И, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв О, Е, А, И использовали соответственно кодовые слова 01, 110, 1010, 001. Найдите наименьшую возможную суммарную длину всех кодовых слов.

Автомат обрабатывает десятичное натуральное число N по следующему алгоритму:

1) Строится двоичная запись числа N.
2) К этой записи справа дописывается 0, если число нечетное, и слева 1 в обратном случае.
3) Если единиц в двоичном числе получилось четное количество, справа дописывается 1, иначе 0.

Например, двоичная запись 1010 числа 10 будет преобразована в 110100.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма.
Укажите минимальное число N, для которого результат работы алгоритма будет больше 228. В ответе это число запишите в десятичной системе счисления.

Найдите битовую глубину кодирования растрового изображения размером 512x300 пикселей, которое занимает 600 Кбайт. В ответе запишите только целое число, единицу измерения писать не нужно.

Все 4-буквенные слова, составленные из букв П, Р, В, Д, А, записаны в алфавитном порядке и пронумерованы. Вот начало списка:

1. АААА
2. АААВ
3. АААД
4. АААП
5. АААР
6. ААВА
...

Найдите номер первого слова в этом списке, которое не содержит гласных и одинаковых букв.

Автомобильный номер состоит из одиннадцати букв русского алфавита A, B, C, E, H, K, M, O, P, T, X и десятичных цифр от 0 до 9. Каждый номер состоит из двух букв, затем идет 3 цифры и еще одна буква. Например, АВ901С. В системе каждый такой номер кодируется посимвольно, при этом каждая буква и каждая цифра кодируются одинаковым минимально возможным количеством бит. Укажите, на сколько бит можно уменьшить размер памяти, выделенной для хранения одного номера, если кодировать с помощью минимально возможного количества бит каждую из трех групп – первые две буквы, три цифры и последняя буква.

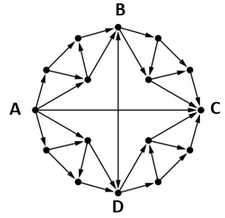
На рисунке представлена схема дорог, связывающих города A, B, C, D. По каждой дороге можно двигаться только один раз в направлении стрелки. По дороге из B в D можно двигаться в любую сторону, но лишь один раз. Сколько существует различных путей из города A в город C, проходящих либо через В (но не D), либо через D (но не B), либо через B и D одновременно?