Проверочная работа по темам ЕГЭ 1-5 (1 вариант)

На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведе-ния о длине этих дорог в километрах.
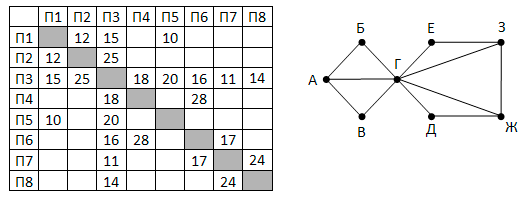Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину более длинной из дорог ЕЗ и ДЖ. В ответе запишите целое число.

Логическая функция F задаётся выражением ¬(b → a) ∧ (c → d) ≠ (a ∧ b ∧ c ∧ ¬d).
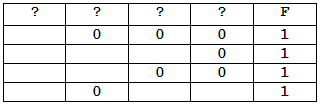На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.

 В файле 3-78.xls приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Таблица «Магазин» содержит информацию о местонахождении магазинов. На рисунке приведена схема указанной базы данных.
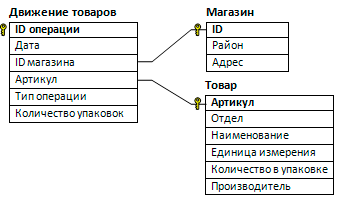Используя информацию из приведённой базы данных, определите на сколько увеличилось количество упаковок кофе всех сортов, имеющихся в наличии в магазинах Заречного района, за период с 3 по 8 июня включительно.

По каналу связи передаются сообщения, содержащие только семь букв: О, К, Т, Я, Б, Р, Ь. Для передачи используется двоичный код, допускающий однозначное декодирование. Кодовые слова для некоторых букв известны: К – 1010, Т – 100, Б – 0101, Р – 110, Ь – 001. Укажите минимальную возможную сумму длин кодов всех букв.

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1) Строится двоичная запись числа N.
2) К этой записи дописываются ещё несколько разрядов по следующему правилу:
   а) если N чётное, то к нему справа приписывается в двоичном виде сумма цифр его двоичной записи;
   б) если N нечётное, то к нему справа приписываются два нуля, а слева единица.
Например, двоичная запись числа 1101 будет преобразована в 1110100.
Полученная таким образом запись (в ней как минимум на один разряд больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите наибольшее число N, для которого результат работы данного алгоритма меньше 1000. В ответе это число запишите в десятичной системе счисления.