Определенный интеграл

Список вопросов теста
Вопрос 1
Отметьте верные утверждения
Варианты ответов
- определенный интеграл есть число
- неопределенный интеграл есть число
- постоянный множитель можно выносить за знак определенного интеграла
Вопрос 2

Варианты ответов
- 2
- -1
- 1,5
- 1
- 0
Вопрос 3

Варианты ответов
- 12
- 16
- 1
- 84
- 56
Вопрос 4

Варианты ответов
Вопрос 5

Варианты ответов
- 4/3
- 4
- 3
-
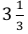
Вопрос 6
Формула Ньютона-Лейбница
Варианты ответов
Вопрос 7
Вычислить интеграл: 
Варианты ответов
- 2,5
- 1,5
- 0
-
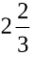
Вопрос 8
Вычислить: 
Варианты ответов
- 2ln2
- ln3
- ln2
-
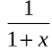
Вопрос 9

Площадь фигуры, изображенной на рисунке, определяется формулой:
Варианты ответов
Вопрос 10

Варианты ответов
Вопрос 11
Вычислить: 
Варианты ответов
Вопрос 12

Площадь фигуры, изображенной на рисунке, определяется формулой:
Варианты ответов
Вопрос 13
Вычислить: 
Варианты ответов
- 2
- 1
- 0
- -2
Вопрос 14
Каким способом решать итегралы?
Установить соответствие.
1.

2.

3.

Варианты ответов
- метод подстановки
- непосредственное интегрирование
- метод интегрирования по частям
- подстановка Эйлера
Вопрос 15
Отметьте свойства определенного интеграла
Варианты ответов
Вопрос 16
Геометрический смысл определенного интеграла 
Варианты ответов
-
площадь криволинейной трапеции, которая ограничена осью абсцисс, графиком функции
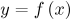 и вертикальными прямыми x=a и x=b
и вертикальными прямыми x=a и x=b -
площадь прямоугольника
-
периметр трапеции
Вопрос 17
Физический смысл определенного интеграла 
Варианты ответов
-
площадь криволинейной трапеции, которая ограничена осью абсцисс, графиком функции
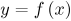 и вертикальными прямыми x=a и x=b
и вертикальными прямыми x=a и x=b -
путь, пройденный точкой за промежуток времени от а до в равен определенному интегралу от скорости
-
мгновенная скорость материальной точки в определенный момент времени
Вопрос 18
Задачи, приводящие к понятию определенного интеграла
Варианты ответов
- задача о площади криволинейной трапеции
- задача о массе неоднородного стержня
- задача о перемещении точки
- задача о кратчайшем пути
Вопрос 19
Каким методом решать данный интеграл: 
Варианты ответов
- непосредственного интегрирования
- по частям
- методом подстановки
Вопрос 20
Каким методом решать данный интеграл: 
Варианты ответов
- непосредственного интегрирования
- по частям
- методом подстановки
Получите комплекты видеоуроков + онлайн версии
 0
0 3084
3084 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход




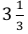




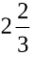
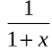




















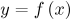 и вертикальными прямыми x=a и x=b
и вертикальными прямыми x=a и x=b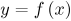 и вертикальными прямыми x=a и x=b
и вертикальными прямыми x=a и x=b








