ЕГЭ тест №26 (Вариант № 4014)

Список вопросов теста
Вопрос 1
На рисунке слева изображена схема дорог Н-ского района, в таблице звёздочкой обозначено наличие дороги из одного населённого пункта в другой. Отсутствие звёздочки означает, что такой дороги нет.
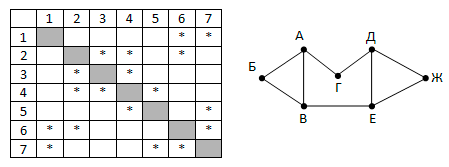
Определите, какие номера населённых пунктов в таблице могут соответствовать населённым пунктам В и Е на схеме. В ответе запишите эти два номера в возрастающем порядке без пробелов и знаков препинания.
Вопрос 2
Логическая функция F задаётся выражением (⌐x ∧ y ≡ z) ∧ w.
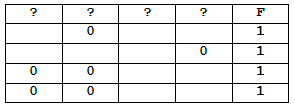
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Вопрос 3
В файле 3-5.xls приведён фрагмент базы фрагмент базы данных «Аудиотека». База данных состоит из четырёх таблиц. Таблица «Альбомы» содержит записи о записанных альбомах, а также информацию о исполнителях. Таблица «Артисты» содержит записи о названии исполнителей. Таблица «Треки» содержит записи о записанных композициях, а также информацию о альбомах и жанрах. Поле Длительность содержит длительность аудиозаписи в миллисекундах, поле Размер содержит размер аудиозаписи в байтах, а поле Стоимость содержит стоимость аудиозаписи в рублях. Таблица «Жанры» содержит данные о названии жанров. На рисунке приведена схема указанной базы данных.
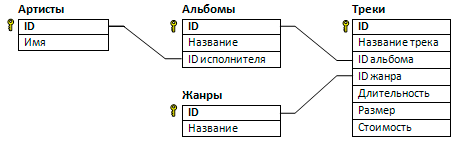 Используя информацию из приведённой базы данных, определите, сколько рублей стоит самый дешёвый альбом группы Red Hot Chili Peppers. Стоимость альбома оценивается как сумма стоимости входящих в него треков.
Используя информацию из приведённой базы данных, определите, сколько рублей стоит самый дешёвый альбом группы Red Hot Chili Peppers. Стоимость альбома оценивается как сумма стоимости входящих в него треков.
Вопрос 4
Известно, что слово КАШКА закодировали с помощью последовательности 1110110011101. При этом код удовлетворяет условию Фано. Найдите минимальную длину кодовой последовательности для слова ПАМПУШКА? Известно, что другие буквы в кодируемой последовательности встретиться не могут.
Вопрос 5
Автомат обрабатывает десятичное натуральное число N по следующему алгоритму:
1) Строится двоичная запись числа N.
2) К этой записи справа дописывается 0, если число нечетное, и слева 1 в обратном случае.
3) Если единиц в двоичном числе получилось четное количество, справа дописывается 1, иначе 0.
Например, двоичная запись 1010 числа 10 будет преобразована в 110100.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма.
Укажите минимальное число N, для которого результат работы алгоритма будет больше 228. В ответе это число запишите в десятичной системе счисления.
Вопрос 6
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Налево m (где m – целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 10 [Налево 60 Вперёд 300 Налево 60]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии следует учитывать.
Вопрос 7
Автоматическая фотокамера каждую секунду создаёт растровое изображение, содержащее 216=65536 цветов. Размер изображения – 640×480 пикселей. Все полученные изображения и коды пикселей внутри одного изображения записываются подряд, никакая дополнительная информация не сохраняется, данные не сжимаются. Сколько Мбайт нужно выделить для хранения всех изображений, полученных за 128 секунд? В ответе укажите только целое число – количество Мбайт, единицу измерения указывать не надо.
Вопрос 8
Миша составляет 6-буквенные коды из букв Б, А, Л, О, Н. Каждая допустимая гласная буква может входить в код не более одного раза. Сколько кодов может составить Миша?
Вопрос 9
Откройте файл электронной таблицы 9-0.xls, содержащей результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время наблюдений суточные колебания температуры (разность между максимальной и минимальной температурой в течение суток) не превышали 15 градусов.
Вопрос 10
С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «письмо» или «Письмо» (в любом падеже единственного и множественного числа) в тексте романа А.С. Пушкина «Капитанская дочка» (файл 10-34.docx). В ответе укажите только число.
Вопрос 11
Каждый сотрудник предприятия получает электронный пропуск, на котором записаны личный код, состоящий из двух частей. Первая часть кода содержит 10 символов, каждый из которых может быть одной из 26 заглавных латинских букв. Вторая часть кода содержит 8 символов, каждый из которых может быть одной из десятичных цифр. При этом в базе данных сервера формируется запись, содержащая этот код и дополнительную информацию о пользователе. Для представления кода используют посимвольное кодирование, все символы в пределах одной части кода кодируют одинаковым минимально возможным для этой части количеством битов, а для кода в целом выделяется минимально возможное целое количество байтов. Для хранения данных о 60 пользователях потребовалось 1980 байт. Сколько байтов выделено для хранения дополнительной информации об одном пользователе? В ответе запишите только целое число – количество байтов.
Вопрос 12
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 125 идущих подряд цифр 8? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (333) ИЛИ нашлось (888)
ЕСЛИ нашлось (333)
ТО заменить (333, 8)
ИНАЧЕ заменить (888, 3)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Вопрос 13
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Какова длина самого длинного маршрута, начинающегося и заканчивающегося в пункте Ж и не проходящих дважды через один и тот же пункт? Длиной пути считать количество дорог, составляющих этот путь.
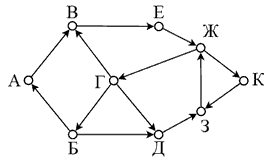
Вопрос 14
Решите уравнение
121x + 1 = 1017
Ответ запишите в троичной системе счисления. Основание системы счисления указывать не нужно.
Вопрос 15
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула
ДЕЛ(x, A) → (ДЕЛ(x, 14) ∧ ДЕЛ(x, 21))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Вопрос 16
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = G(1) = 1 F(n) = 2·F(n–1) + G(n–1) – 2, если n > 1 G(n) = F(n–1) + 2·G(n–1), если n > 1
Чему равно значение F(14) + G(14)?
Вопрос 17
В файле 17-1.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10 000 до 10 000 включительно. Определите и запишите в ответе сначала наибольшую длину убывающей подпоследовательности, затем количество убывающих подпоследовательностей такой длины. Под убывающей подпоследовательностью подразумевается последовательность подряд идущих элементов, каждый из которых меньше предыдущего. Например, в последовательности (7, -12, 10, 4, 7, -12, 10, -12, 3) наибольшая длина убывающей подпоследовательности равна 2, количество таких подпоследовательностей равно 4.
Вопрос 18
Дана последовательность вещественных чисел. Из неё необходимо выбрать несколько подряд идущих чисел так, чтобы каждое следующее число отличалось от предыдущего не более чем на 2. Какую максимальную сумму могут иметь выбранные числа? В ответе запишите только целую часть максимально возможной суммы.
Исходные данные записаны в виде столбца электронной таблицы в файле 18-77.xls.
Вопрос 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в любую кучу один камень или увеличить количество камней в первой куче в два раза или увеличить количество камней во второй куче в три раза. Игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 30. Победителем считается игрок, сделавший последний ход. В начальный момент в первой куче было K≥1 камней, а во второй – S≥1 камней, K+S ≤ 29.
Ответьте на следующие вопросы:
Вопрос 1. Сколько существует пар (K; S), таких что Ваня выигрывает первым ходом при любой игре Пети?
Вопрос 20
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в любую кучу один камень или увеличить количество камней в первой куче в два раза или увеличить количество камней во второй куче в три раза. Игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 30. Победителем считается игрок, сделавший последний ход. В начальный момент в первой куче было K≥1 камней, а во второй – S≥1 камней, K+S ≤ 29.
Ответьте на следующие вопросы:
Вопрос 2. При S=7, найдите минимальное и максимальное значение K, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Вопрос 21
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в любую кучу один камень или увеличить количество камней в первой куче в два раза или увеличить количество камней во второй куче в три раза. Игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 30. Победителем считается игрок, сделавший последний ход. В начальный момент в первой куче было K≥1 камней, а во второй – S≥1 камней, K+S ≤ 29.
Ответьте на следующие вопросы:
Вопрос 3. При K=1 найдите такое значение S, при котором, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Вопрос 22
Исполнитель Калькулятор преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1 2. Умножить на 2
Программа для исполнителя Калькулятор – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 21 и при этом траектория вычислений не содержит число 10?
Получите комплекты видеоуроков + онлайн версии
 0
0 1415
1415 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








