ЕГЭ тест №25 (Вариант № 65645)

Список вопросов теста
Вопрос 1
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
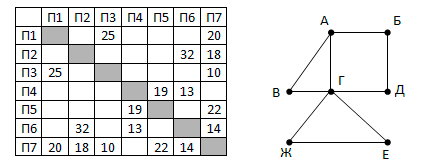
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего пути из пункта Г в пункт Д.
Вопрос 2
Логическая функция F задаётся выражением (x ≡ ¬z) → ((x ∨ w) ≡ y).
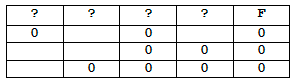
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Вопрос 3
В файле 3-5.xls приведён фрагмент базы фрагмент базы данных «Аудиотека». База данных состоит из четырёх таблиц. Таблица «Альбомы» содержит записи о записанных альбомах, а также информацию о исполнителях. Таблица «Артисты» содержит записи о названии исполнителей. Таблица «Треки» содержит записи о записанных композициях, а также информацию о альбомах и жанрах. Поле Длительность содержит длительность аудиозаписи в миллисекундах, поле Размер содержит размер аудиозаписи в байтах, а поле Стоимость содержит стоимость аудиозаписи в рублях. Таблица «Жанры» содержит данные о названии жанров. На рисунке приведена схема указанной базы данных.
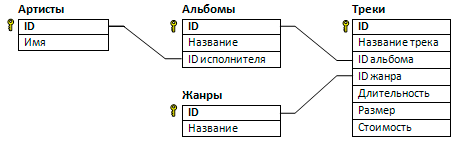 Используя информацию из приведённой базы данных, определите, сколько минут длится самый продолжительный альбом группы Nirvana. В ответе укажите целую часть получившегося числа.
Используя информацию из приведённой базы данных, определите, сколько минут длится самый продолжительный альбом группы Nirvana. В ответе укажите целую часть получившегося числа.
Вопрос 4
По каналу связи передаются сообщения, содержащие только четыре буквы: А, Б, В, Г; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв А и Б используются такие кодовые слова: А – 1; Б – 011. Укажите сумму длин кратчайших кодовых слов для букв В и Г, при котором код будет допускать однозначное декодирование.
Вопрос 5
Автомат обрабатывает натуральное число N по следующему алгоритму:
1) Строится двоичная запись числа N.
2) Запись «переворачивается», то есть читается справа налево. Если при этом появляются ведущие нули, они отбрасываются.
3) Полученное число переводится в десятичную систему счисления и выводится на экран.
Какое наибольшее число, не превышающее 100, после обработки автоматом даёт результат 7?
Вопрос 6
Определите наименьшее и наибольшее введённое значение переменной s, при котором программа выведет число 729. В ответ запишите оба числа в порядке убывания без пробелов и других разделителей.
s = int(input())
n = 1
while s < 185:
s = s + 30
n = n * 3
print(n)
Вопрос 7
Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 50 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 2 раза больше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 2 раза меньше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б?
Вопрос 8
Петя составляет шестибуквенные слова перестановкой букв слова АДЖИКА. При этом он избегает слов с двумя подряд одинаковыми буквами. Сколько всего различных слов может составить Петя?
Вопрос 9
Откройте файл электронной таблицы 9-0.xls, содержащей результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз в июне максимальная температура в течение суток оказывалась выше минимальной на 15 и более градусов. В ответе введите только одно число – количество таких дней.
Вопрос 10
С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «сердце» или «Сердце» в тексте романа в стихах А.С. Пушкина «Евгений Онегин» (файл 10-0.docx). Другие формы слова «сердце», такие как «сердцу», «сердцем» и т.д., учитывать не следует. В ответе укажите только число.
Вопрос 11
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 10 символов и содержащий только символы из 26-символьного латинского алфавита. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 6 байт на одного пользователя. Определите объём памяти (в байтах), необходимый для хранения сведений о 30 пользователях.
Вопрос 12
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (111) ИЛИ нашлось (222)
заменить (111, 2)
заменить (222, 1)
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой программы к строке вида 1…12…2 (2018 единиц и 2019 двоек)?
Вопрос 13
На рисунке представлена схема дорог, связывающих города A, B, C, D, E, F, G, H, K, L, M. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует маршрутов из А в H, которые проходят через пункт С или пункт L?
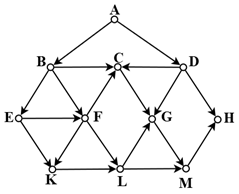
Вопрос 14
Выражение ((44 + 450)·425 + 44)·412 + 44 записано в системе счисления с основанием 4. Определите, сколько в этой записи цифр 0.
Вопрос 15
На числовой прямой даны два отрезка: P = [15, 37] и Q = [30, 45]. Найдите наибольшую возможную длину отрезка A, при котором формула
(¬(x ∈ P) ∨ (x ∈ Q)) → ¬(x ∈ A)
тождественно истинна, то есть принимает значение 1 при любых x.
Вопрос 16
Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями:
F(n) = 1, при n < 2, F(n) = F(n/3) + 1, когда n ≥ 2 и делится на 3, F(n) = F(n - 2) + 5, когда n ≥ 2 и не делится на 3.
Назовите количество значений n на отрезке [1;100000], для которых F(n) равно 55.
Вопрос 17
В файле 17-1.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар, в которых один элемента меньше, чем среднее арифметическое всех чисел в файле, а второй – больше, чем среднее арифметическое всех чисел в файле. В ответе запишите два числа: сначала количество найденных пар, а затем – максимальную сумму элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
Вопрос 18
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в любую кучу один камень или увеличить количество камней в любой куче в четыре раза. Игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 125. Победителем считается игрок, сделавший последний ход. В начальный момент в первой куче было 7 камней, а во второй – S камней, 1 ≤ S ≤ 117.
Ответьте на следующие вопросы:
Вопрос 1. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
Вопрос 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в любую кучу один камень или увеличить количество камней в любой куче в четыре раза. Игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 125. Победителем считается игрок, сделавший последний ход. В начальный момент в первой куче было 7 камней, а во второй – S камней, 1 ≤ S ≤ 117.
Ответьте на следующие вопросы:
Вопрос 2. Найдите минимальное и максимальное значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Вопрос 20
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в любую кучу один камень или увеличить количество камней в любой куче в четыре раза. Игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 125. Победителем считается игрок, сделавший последний ход. В начальный момент в первой куче было 7 камней, а во второй – S камней, 1 ≤ S ≤ 117.
Ответьте на следующие вопросы:
Вопрос 3. Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Вопрос 21
Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наибольшее число x, при вводе которого алгоритм печатает сначала 5, а потом 8.
x = int(input())
L = 0
M = 0
while x > 0:
M = M + 1
if x % 2 != 0:
L = L + 1
x = x // 2
print(L)
print(M)
Вопрос 22
Исполнитель Калькулятор преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1 2. Прибавить 3
Программа для исполнителя Калькулятор – это последовательность команд. Сколько существует программ, для которых при исходном числе 3 результатом является число 21 и при этом траектория вычислений содержит число 12 и не содержит числа 18?
Получите комплекты видеоуроков + онлайн версии
 0
0 549
549 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








