ЕГЭ тест №23 (Вариант № 49744)
Список вопросов теста
Вопрос 1
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
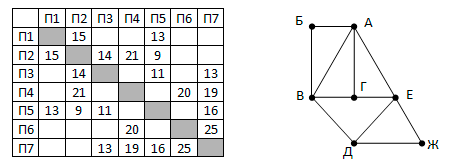
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, в какой пункт ведёт самая короткая дорога из пункта А.
Вопрос 2
Логическая функция F задаётся выражением ¬w ∧ (x ∧ ¬z ∨ ¬x ∧ ¬y ∧ z).
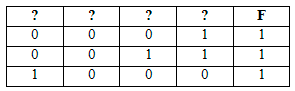
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Вопрос 3
В файле 3-54.xls приведён фрагмент базы данных «Фильмы». Таблица «Фильмы» содержит информацию о названии фильма, продолжительности фильма в секундах, бюджете фильма (в долларах) и о сборах с его показа (в долларах). Таблица «Режиссёры» содержит информацию о режиссёре, а таблица «Жанры» – жанрах, к которым могут относится фильмы. Поле ID в каждой таблице обозначает код объекта. На рисунке приведена схема указанной базы данных.
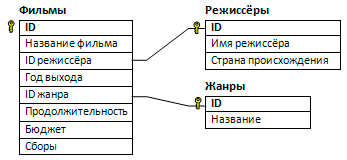
Используя информацию из приведённой базы данных, определите суммарный бюджет в миллионах долларов всех фильмов в жанре Триллер, снятых режиссёрами из Великобритании в период с 2000 года по 2012 год? В ответ запищите только целую часть числа.
Вопрос 4
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я . Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А – 11, Б – 101, Я – 010. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ГРАММ?
Вопрос 5
Автомат обрабатывает натуральное число N < 256 по следующему алгоритму:
1) Строится восьмибитная двоичная запись числа N.
2) Инвертируются все разряды исходного числа, кроме последней единицы и стоящих за ней нулей (0 заменяется на 1, 1 на 0).
3) Полученное число переводится в десятичную систему счисления.
Для какого значения N результат работы алгоритма равен 221?
Вопрос 6
Определите наибольшее введённое значение переменной n, при котором программа выведет число 45.
n = int(input())
s = 350
while 2*s+n < 1100:
s = s - 5
n = n + 15
print(s)
Вопрос 7
Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 75 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3 раза выше и частотой дискретизации в 2,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной записи.
Вопрос 8
Из букв слова К О Р Т И К составляются 6-буквенные последовательности. Сколько можно составить различных последовательностей, если известно, что в каждой из них содержится не менее 3 согласных?
Вопрос 9
Откройте файл электронной таблицы 9-0.xls, содержащей результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Найдите количество дней, когда температура в 21:00 была выше, чем средняя температура в этот день.
Вопрос 10
С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «мысль» или «Мысль» (в любых падежах единственного и множественного числа) в тексте произведения А.С. Пушкина «Дубровский» (файл 10-106.docx). В ответе укажите только число.
Вопрос 11
Каждый сотрудник предприятия получает электронный пропуск, на котором записаны личный код, состоящий из двух частей. Первая часть кода содержит 15 символов, каждый из которых может быть одной из 26 заглавных латинских букв. Вторая часть кода содержит 8 символов, каждый из которых может быть одной из десятичных цифр. При этом в базе данных сервера формируется запись, содержащая этот код и дополнительную информацию о пользователе. Для представления кода используют посимвольное кодирование, все символы в пределах одной части кода кодируют одинаковым минимально возможным для этой части количеством битов, а для кода в целом выделяется минимально возможное целое количество байтов. Для хранения данных о 35 пользователях потребовалось 3150 байт. Сколько байтов выделено для хранения дополнительной информации об одном пользователе? В ответе запишите только целое число – количество байтов.
Вопрос 12
Какая строка получится в результате применения этой программы к строке, состоящей из цифры 1, за которой следуют 80 идущих подряд цифр 8? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (18) ИЛИ нашлось (288) ИЛИ нашлось (3888)
ЕСЛИ нашлось (18)
ТО заменить (18, 2)
ИНАЧЕ
ЕСЛИ нашлось (288)
ТО заменить (288, 3)
ИНАЧЕ заменить (3888, 1)
КОНЕЦ ЕСЛИ
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Вопрос 13
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город М и проходящих через город В?
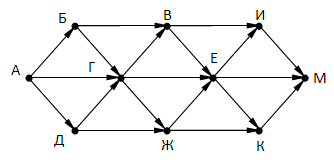
Вопрос 14
Некоторое число X из десятичной системы счисления перевели в системы счисления с основаниями 16, 8 и 4. Часть символов при записи утеряна. Позиции утерянных символов обозначены символом *:
X = *7*16 = 5*68 = ***1*4
Вопрос 15
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула
(A < 50) ∧ (¬ДЕЛ(x, A) → (ДЕЛ(x, 10) → ¬ДЕЛ(x, 18)))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Вопрос 16
Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями:
F(n) = 1, при n < 2, F(n) = F(n/3) - 1, когда n ≥ 2 и делится на 3, F(n) = F(n - 1) + 17, когда n ≥ 2 и не делится на 3.
Назовите минимальное значение n, для которого F(n) равно 110.
Вопрос 17
В файле 17-2.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10 000 до 10 000 включительно. Определите и запишите в ответе сначала количество элементов последовательности, которые равны её наименьшему элементу, затем позицию последнего такого элемента в последовательности при подсчёте с единицы. Например, в последовательности 7; -12; 10; 4; 7; -12; 10; -12; 3 три элемента равны минимальному, позиция последнего из них - 8. Ответом для данного примера будет пара чисел 3 и 8.
Вопрос 18
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
а) добавить в кучу один камень;
б) добавить в кучу два камня;
в) добавить в кучу три камня;
г) увеличить количество камней в куче в два раза.
Игра завершается в тот момент, когда количество камней в куче превышает 37. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 38 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 37.
Ответьте на следующие вопросы:
Вопрос 1. Найдите значение S, при котором Ваня выигрывает своим первым ходом при любой игре Пети.
Вопрос 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
а) добавить в кучу один камень;
б) добавить в кучу два камня;
в) добавить в кучу три камня;
г) увеличить количество камней в куче в два раза.
Игра завершается в тот момент, когда количество камней в куче превышает 37. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 38 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 37.
Ответьте на следующие вопросы:
Вопрос 2. Найдите минимальное и максимальное значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Вопрос 20
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
а) добавить в кучу один камень;
б) добавить в кучу два камня;
в) добавить в кучу три камня;
г) увеличить количество камней в куче в два раза.
Игра завершается в тот момент, когда количество камней в куче превышает 37. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 38 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 37.
Ответьте на следующие вопросы:
Вопрос 3. Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Вопрос 21
Сколько существует таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 12.
x = int(input())
a = 0
b = 0
while x > 0:
a = a + 1
b = b + (x % 10)
x = x // 10
print(a)
print(b)
Вопрос 22
Исполнитель Калькулятор преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1 2. Прибавить 2 3. Прибавить 3
Программа для исполнителя Калькулятор – это последовательность команд. Сколько существует программ, для которых при исходном числе 3 результатом является число 15, и при этом траектория вычислений не содержит число 8?
Получите комплекты видеоуроков + онлайн версии
 0
0 1697
1697 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








