ЕГЭ тест №17 (Вариант № 22599)
Список вопросов теста
Вопрос 1
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
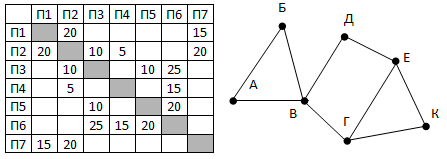 Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего пути из пункта В в пункт Е.
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего пути из пункта В в пункт Е.
Вопрос 2
Логическая функция F задаётся выражением ¬w ∧ (x ∧ ¬z ∨ ¬x ∧ ¬y ∧ z).
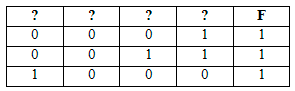
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Вопрос 3
В файле 3-30.xls приведён фрагмент базы фрагмент базы данных «Русский рок», описывающей советские и российские рок-группы. База данных состоит из двух таблиц. Таблица «Группы» содержит информацию о музыкальных коллективах: ID, название, год основания. Таблица «Альбомы» содержит информацию о студийных музыкальных альбомах: ID, название, ID группы, год издания, количество песен. Для каждой группы в базе данных указано ровно 3 альбома. На рисунке приведена схема базы данных.
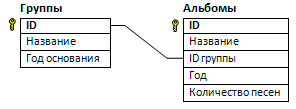
Используя информацию из приведённой базы данных, найдите альбомы, выпущенные в год, в который было выпущено максимальное количество альбомов. В ответе укажите год основания группы, выпустившей в найденный год альбом с первым по алфавиту названием среди всех подходящих альбомов.
Вопрос 4
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, Ж, З, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г, Д, Е, Ж использовали соответственно кодовые слова 11, 0010, 1011, 01, 0011, 000, 1010. Укажите кратчайшее возможное кодовое слово для буквы З, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Вопрос 5
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописывается (дублируется) последняя цифра.
3) Затем справа дописывается 0, если в двоичном коде числа N чётное число единиц, и 1, если нечётное.
4) К полученному результату дописывается ещё один бит чётности так, чтобы количество единиц в двоичной записи полученного числа стало чётным.
Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число N, после обработки которого автомат получает число, большее 90. В ответе это число запишите в десятичной системе.
Вопрос 6
Запишите число, которое будет напечатано в результате выполнения следующей программы.
n = 1
s = 0
while n <= 650:
s = s + 20
n = n * 5
print(s)
Вопрос 7
Камера снимает видео без звука с частотой 48 кадров в секунду, при этом изображения используют палитру, содержащую 4096 цвета. 1 минута видео в среднем занимает 18 Мегабайт. При записи файла на сервер полученное видео преобразуют так, что его частота кадров уменьшается до 24 кадров в секунду, а изображения преобразуют в формат, содержащий палитру из 16 цветов. Другие преобразования и иные методы сжатия не используются. Сколько минут преобразованного видео в среднем можно записать при ограничении размера видеозаписи в 48 Мегабайт?
Вопрос 8
Разведчик кодирует символы текста пятью стрелками. Каждая стрелка может иметь четыре положения (направления): ↑→↓←. Для первой стрелки запрещено положение вверх: ↑. Некоторые стрелки не могут находиться в одинаковом положении (направлении): первая и пятая, вторая и четвертая. Сколько всего различных символов текста может закодировать разведчик?
Вопрос 9
Откройте файл электронной таблицы 9-123.xls, содержащей в каждой строке четыре натуральных числа. Выясните, какое количество четверок чисел может являться последовательностью углов (в градусах) вписанного четырехугольника. В ответе запишите только число.
Вопрос 10
В файле 10-141.docx приведена книга Н.В. Гоголя «Вечера на хуторе близ Диканьки». Сколько раз слово «хлопец» (во всех формах единственного и множественного числа) встречается в тексте повести «Страшная месть» (не считая сносок)? Регистр написания слова не имеет значения. В ответе укажите только число.
Вопрос 11
В некоторой стране автомобильный номер длиной 11 символов составляется из заглавных букв (всего используется 25 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным целым количеством байт. Определите объем памяти в байтах, необходимый для хранения 85 автомобильных номеров.
Вопрос 12
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город М и проходящих через город Г?
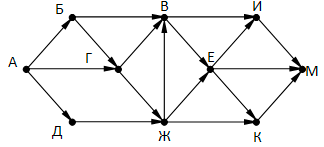
Вопрос 13
Значение выражения 7103 – 6∙770 + 3∙757 – 98 записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи?
Вопрос 14
Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение
( (X & 13 ≠ 0) ∧ (X & 39 ≠ 0)) → ((X & A ≠ 0) ∧ (X & 13 ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Вопрос 15
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч три камня или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 72. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 72 или больше камней.
В начальный момент в первой куче было 7 камней, во второй куче – S камней, 1 ≤ S ≤ 64. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 1. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
Вопрос 16
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч три камня или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 72. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 72 или больше камней.
В начальный момент в первой куче было 7 камней, во второй куче – S камней, 1 ≤ S ≤ 64. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 2. Укажите минимальное значение S, при котором у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Вопрос 17
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч три камня или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 72. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 72 или больше камней.
В начальный момент в первой куче было 7 камней, во второй куче – S камней, 1 ≤ S ≤ 64. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 3. Найдите два значения S, при которых у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Найденные значения запишите в ответе в порядке возрастания через пробел.
Вопрос 18
Ниже на трёх языках программирования записан алгоритм. Получив на вход число X, этот алгоритм печатает одно число. Укажите наименьшее число Х, большее 80, при вводе которого алгоритм печатает число 17.
x = int(input())
s = 0
while x > 0:
s = s + x % 9
x = x // 3
print(s)
Вопрос 19
Исполнитель Калькулятор преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1 2. Прибавить 2 3. Умножить на 3
Программа для исполнителя Калькулятор – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 15, и при этом траектория вычислений содержит числа 4 и 11?
Получите комплекты видеоуроков + онлайн версии
 0
0 2114
2114 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








