ЕГЭ тест №16 (Вариант № 69211)

Список вопросов теста
Вопрос 1
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
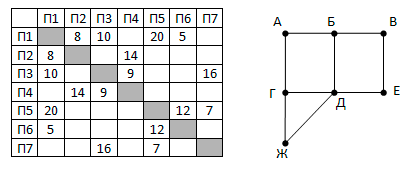
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего пути из пункта А в пункт Е.
Вопрос 2
Логическая функция F задаётся выражением (x ∨ y ∨ ¬z) ∧ (¬x ∨ y ∨ ¬z) ∧ (¬x ∨ ¬y ∨ z). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
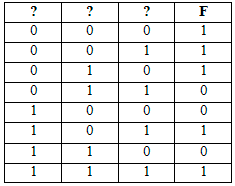
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (без разделителей).
Вопрос 3
В файле 3-30.xls приведён фрагмент базы фрагмент базы данных «Русский рок», описывающей советские и российские рок-группы. База данных состоит из двух таблиц. Таблица «Группы» содержит информацию о музыкальных коллективах: ID, название, год основания. Таблица «Альбомы» содержит информацию о студийных музыкальных альбомах: ID, название, ID группы, год издания, количество песен. Для каждой группы в базе данных указано ровно 3 альбома. На рисунке приведена схема базы данных.
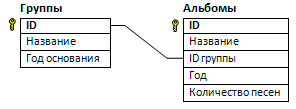
Используя информацию из приведённой базы данных, определите, у скольких групп из указанных в базе данных с момента основания и до выхода первого из указанных альбомов прошло не более 5 лет.
Вопрос 4
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, В, Г, Д, Е и Ж. Для передачи используется двоичный код, удовлетворяющий условию Фано. Для буквы А используется кодовое слово 10; для буквы Б используется кодовое слово 011. Какова минимальная общая длина кодовых слов для всех семи букв?
Вопрос 5
Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом:
1) Строится двоичная запись числа N.
2) Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется цифра, которая встречается реже.
3) Шаг 2 повторяется ещё два раза.
4) Результат переводится в десятичную систему счисления.
При каком наибольшем исходном числе N < 100 в результате работы алгоритма получится число, кратное 4?
Вопрос 6
Сколько существует положительных чисел, подаваемых на вход программе, при которых программа в результате своей работы выведет на экран одно положительное число?
d = int(input())
n = 20
s = 40
while s + n < d:
s = s – 10
n = n - 20
print(n)
Вопрос 7
Автоматическая камера производит растровые изображения размером 800×600 пикселей. Для кодирования цвета каждого пикселя используется одинаковое количество байт, коды пикселей записываются в файл один за другим без промежутков. Объём файла с изображением не может превышать 700 Кбайт без учёта размера заголовка файла. Какое максимальное количество цветов можно использовать в палитре?
Вопрос 8
Леся составляет слова, содержащие ровно 3 буквы М, из букв Ч, О, А, Н, И, М, Е. Слово может иметь длину от 4 до 6 букв. Сколько слов может составить Леся?
Вопрос 9
Откройте файл электронной таблицы 9-0.xls, содержащей результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время наблюдений суточные колебания температуры (разность между максимальной и минимальной температурой в течение суток) не превышали 15 градусов.
Вопрос 10
В файле 10-170.docx приведена повесть-феерия А. Грина «Алые паруса». Сколько раз встречается слово «нет» (с заглавной или строчной буквы) в тексте повести (не считая сносок)? В ответе укажите только число.
Вопрос 11
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 11 символов. В качестве символов используют прописные и строчные буквы латинского алфавита (в нём 26 букв), а также десятичные цифры. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено 13 байт на одного пользователя. В компьютерной системе выделено 1 Кб для хранения сведений о пользователях. О каком наибольшем количестве пользователей может быть сохранена информация в системе? В ответе запишите только целое число – количество пользователей.
Вопрос 12
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, O, Т. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город Т и проходящих через город К?
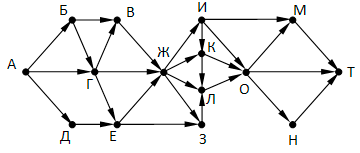
Вопрос 13
Сколько значащих нулей в двоичной записи числа 4230 + 8120 – 2150 – 100?
Вопрос 14
На числовой прямой даны два отрезка: P = [12, 46] и Q = [20, 30]. Найдите наибольшую возможную длину отрезка A, при котором формула
(x ∈ А) ∧ ¬((x ∈ P) ∨ (x ∈ Q))
тождественно ложна, то есть принимает значение 0 при любых x.
Вопрос 15
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в любую кучу один камень или добавить добавить в любую кучу столько камней, сколько их в данный момент в другой куче. Игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 73. Победителем считается игрок, сделавший последний ход. В начальный момент в первой куче было 9 камней, а во второй – S камней, 1 ≤ S ≤ 63.
Ответьте на следующие вопросы:
Вопрос 1. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
Вопрос 16
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в любую кучу один камень или добавить добавить в любую кучу столько камней, сколько их в данный момент в другой куче. Игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 73. Победителем считается игрок, сделавший последний ход. В начальный момент в первой куче было 9 камней, а во второй – S камней, 1 ≤ S ≤ 63.
Ответьте на следующие вопросы:
Вопрос 2. Найдите минимальное и максимальное значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания через пробел.
Вопрос 17
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в любую кучу один камень или добавить добавить в любую кучу столько камней, сколько их в данный момент в другой куче. Игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 73. Победителем считается игрок, сделавший последний ход. В начальный момент в первой куче было 9 камней, а во второй – S камней, 1 ≤ S ≤ 63.
Ответьте на следующие вопросы:
Вопрос 3. Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Вопрос 18
Исполнитель Нолик преобразует двоичное число, записанное на экране. У исполнителя есть две команды, которым присвоены номера:
1. Вычесть 1 2. Убрать последнюю цифру справа
Первая команда уменьшает число на 1. Вторая команда убирает последнюю справа цифру, например, для числа 110 результатом работы данной команды будет являться число 11.
Сколько существует программ, которые исходное двоичное число 110111 преобразуют в двоичное число 110?
Получите комплекты видеоуроков + онлайн версии
 0
0 841
841 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








