ЕГЭ 11Б (в10)

Список вопросов теста
Вопрос 1
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведе-ния о длине этих дорог в километрах.
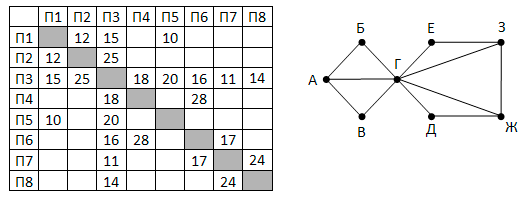
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину более длинной из дорог ЕЗ и ДЖ. В ответе запишите целое число.
Вопрос 2
Логическая функция F задаётся выражением ((w → z) ∧ (¬ x → y)) → ((y ≡ w) ∨ (z ∧ ¬ x)). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Вопрос 3
В файле 3-91.xls приведён фрагмент базы данных базы «Библиотека». База данных состоит из четырёх таблиц. Таблица «Книги» содержит полную информацию о книгах, таблица «Читатели» содержит данные о читателях, таблица «Бронирование» содержит записи о забронированных книгах, таблица «Выдача книг» содержит информацию о выдаче книг и сроках их возвращения.
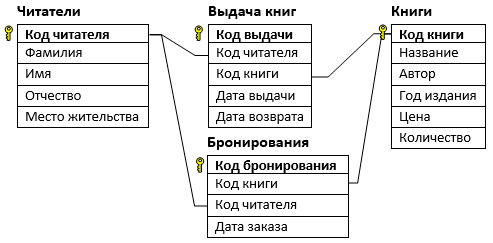
Используя информацию из приведённой базы данных, определите общую стоимость книг «Мёртвые души», забронированных читателями из г. Сочи с 6 по 27 июня.
Вопрос 4
Для кодирования некоторой последовательности, состоящей из букв Е, Л, П, К, Р, C решили использовать неравномерный двоичный код, для которого выполняется условие Фано. Для букв К и Р использовали соответственно кодовые слова 011, 11. Найдите кодовую последовательность наименьшей длины для кодирования слова ПЕРЕПЕЛ и запишите полученный результат в восьмеричном коде. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Вопрос 5
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К полученной записи дописываются разряды. Если в числе четное количество единиц, слева дописывается 1 и справа два нуля, если нечетное – слева дописываются две единицы.
3) Результат переводится в десятичную систему и выводится на экран.
Пример. Дано число N = 13. Алгоритм работает следующим образом:
1. Двоичная запись числа N: 1101.
2.Число единиц нечетное, следовательно слева дописываем две единицы слева – 11 + 1101 = 111101.
3. На экран выводится число 61 = 1111012.
Для какого наименьшего значения N результат работы автомата – число, не меньшее 412?
Вопрос 6
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a; y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1). Цикл
ПОВТОРИ число РАЗ последовательность команд КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным). Чертёжнику был дан для исполнения следующий алгоритм:
ПОВТОРИ 15 РАЗ сместиться на (10, 10) сместиться на (3, -6) сместиться на (-9, 3) КОНЕЦ ПОВТОРИ
Определите, сколько различных точек с целочисленными координатами принадлежат траектории Чертёжника, считая начальную и конечную точки, если исполнитель стартует в точке с целочисленными координатами.
Вопрос 7
Для хранения сжатого аудио файла с заголовком отведено 25 Мбайт памяти. Известно, что фрагмент кодируется в формате стерео, частотой дискретизации 50 кГц и глубиной кодирования 16 бит. После кодирования звуковых дорожек фрагмент сжимается. Сжатый размер закодированного фрагмента меньше исходного на 25%. К сжатому фрагменту дописывается информация о заголовке и дополнительная информация, суммарно занимающая 40 Кбайт. Запишите в ответе целое число - максимальную длительность в минутах фрагмента, который сохраняется по приведенному алгоритму?
Вопрос 8
Ваня составляет 6-буквенные слова из букв В, И, Д, Е, О. Его интересуют коды, в которых есть хотя бы одна буква И и хотя бы одна буква Е. Кроме того, все гласные в слове должны стоять в алфавитном порядке. Сколько различных подходящих кодов может составить Ваня?
Вопрос 9
В файле электронной таблицы 9-168.xls в каждой строке содержатся пять натуральных чисел. Определите количество строк таблицы, в которых хотя бы 3 числа больше среднего арифметического всех чисел в строке.
Вопрос 10
В файле 10-170.docx приведена повесть-феерия А. Грина «Алые паруса». Сколько раз встречается слово «что» (с заглавной или строчной буквы) в тексте повести (не считая сносок)? В ответе укажите только число.
Вопрос 11
При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 252 символов и содержащий только десятичные цифры и символы из 1700-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 4096 идентификаторов. В ответе запишите только целое число – количество Кбайт.
Вопрос 12
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.
1. заменить (v, w) 2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось(333) или нашлось(77777)
ЕСЛИ нашлось(333)
ТО заменить(333,77)
ИНАЧЕ заменить(77777,7)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Исходная строка состояла из семидесяти троек. Определите сумму цифр в строке, полученной в результате работы алгоритма.
Вопрос 13
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует маршрутов, начинающихся и оканчивающихся в пункте Г, не проходящих дважды через один и тот же пункт и не проходящих через город Б?
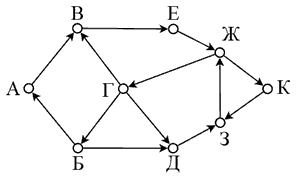
Вопрос 14
Операнды арифметического выражения записаны в системах счисления с основаниями 15 и 17.
123x515 + 67y917
В записи чисел переменными x и y обозначены неизвестные цифры из алфавитов 15-ричной и 17-ричной систем счисления соответственно. Определите значения x, y, при которых значение данного арифметического выражения кратно 131. Для найденных значений x, y вычислите частное от деления значения арифметического выражения на 131 и укажите его в ответе в десятичной системе счисления. Если можно выбрать x, y не единственным образом, возьмите ту пару, в которой значение y меньше. Основание системы счисления в ответе указывать не нужно.
Вопрос 15
Для какого наибольшего целого неотрицательного A выражение
(x + y ≤ 22) ∨ (y ≤ x – 6) ∨ (y ≥ A))
тождественно истинно, т.е. принимает значение 1 при любых целых неотрицательных x и y?
Вопрос 16
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, если n = 1 F(n) = (3·n + 5)·F(n – 1), если n > 1.
Чему равно значение выражения F(2073) / F(2070)
Вопрос 17
В файле 17-336.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от 1 до 100 000 включительно. Обозначим через M минимальный элемент последовательности, кратный 8, но не равный 8. Определите количество пар элементов последовательности, в которых оба числа делятся на M. Гарантируется, что такая пара в последовательности есть. В ответе запишите количество найденных пар, затем максимальное из чисел в такой паре с минимальной суммой элементов. Если пар с минимальной суммой элементов несколько, то следует выбрать максимальное число из первой подходящей пары. В данной задаче под парой подразумевается два идущих подряд элемента последовательности. (ответ ввести через пробел)
Вопрос 18
Квадрат разлинован на N×N клеток (1 < N < 20). В правом верхнем углу квадрата стоит ладья. За один ход ладья может переместиться в пределах квадрата на любое количество клеток влево или вниз (вправо и вверх ладья ходить не может). Определите минимальную и максимальную сумму чисел в клетках, в которых может остановиться ладья при перемещении из правого верхнего угла в левый нижний. В ответе укажите два числа – сначала максимальную сумму, затем минимальную (ответ ввести через пробел).
Исходные данные записаны в файле 18-101.xls в виде прямоугольной таблицы, каждая ячейка которой соответствует клетке квадрата.
Вопрос 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить три камня или увеличить количество камней в куче в три раза. При этом нельзя повторять ход, который только что сделал второй игрок. Например, если в начале игры в куче 4 камня, Петя может первым ходом получить кучу из 5, 7 или 12 камней. Если Петя добавил 1 камень и получил кучу из 5 камней, то следующим ходом Ваня может либо добавить 3 камня (и получить 8 камней), либо утроить количество камней в куче (их станет 15). Получить 6 камней Ваня не может, так как для этого нужно добавить 1 камень, а такой ход только что сделал Петя.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 76. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 76 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 75.
Ответьте на следующие вопросы:
Вопрос 1. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Вопрос 20
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить три камня или увеличить количество камней в куче в три раза. При этом нельзя повторять ход, который только что сделал второй игрок. Например, если в начале игры в куче 4 камня, Петя может первым ходом получить кучу из 5, 7 или 12 камней. Если Петя добавил 1 камень и получил кучу из 5 камней, то следующим ходом Ваня может либо добавить 3 камня (и получить 8 камней), либо утроить количество камней в куче (их станет 15). Получить 6 камней Ваня не может, так как для этого нужно добавить 1 камень, а такой ход только что сделал Петя.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 76. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 76 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 75.
Ответьте на следующие вопросы:
Вопрос 2. Определите минимальное и максимальное значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания (ответы запишите через пробел).
Вопрос 21
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить три камня или увеличить количество камней в куче в три раза. При этом нельзя повторять ход, который только что сделал второй игрок. Например, если в начале игры в куче 4 камня, Петя может первым ходом получить кучу из 5, 7 или 12 камней. Если Петя добавил 1 камень и получил кучу из 5 камней, то следующим ходом Ваня может либо добавить 3 камня (и получить 8 камней), либо утроить количество камней в куче (их станет 15). Получить 6 камней Ваня не может, так как для этого нужно добавить 1 камень, а такой ход только что сделал Петя.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 76. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 76 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 75.
Ответьте на следующие вопросы:
Вопрос 3. Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Вопрос 22
В файле 22-8e.xls содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
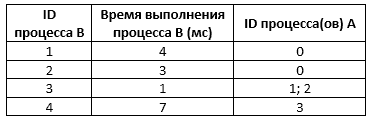
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 – через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
Вопрос 23
Исполнитель преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера:
1. Умножь на 5 2. Умножь на 3 3. Прибавь 45
Первая команда умножает число на экране на 5, вторая – умножает на 3, третья – увеличивает на 45. Сколько существует различных программ, которые преобразуют исходное число 1 в число 2970, и при этом траектория вычислений не более 4 команд «умножь на 5», не менее 2 команд «умножь на 3», и ровно 5 команд «прибавь 45»?
Вопрос 24
Текстовый файл 24-215.txt содержит строку из символов A, B, C и цифр 1, 2, 3, всего не более чем 106 символов. Определите максимальное количество идущих подряд троек символов вида «цифра + буква + цифра».
Получите комплекты видеоуроков + онлайн версии
 0
0 2037
2037 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








