ЕГЭ 10Б (в10)

Список вопросов теста
Вопрос 1
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведе-ния о длине этих дорог в километрах.
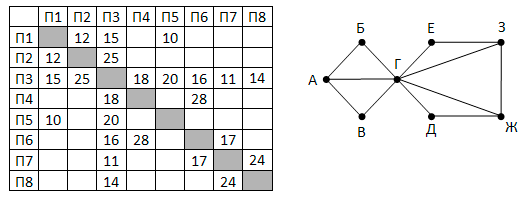
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину более длинной из дорог ЕЗ и ДЖ. В ответе запишите целое число.
Вопрос 2
Логическая функция F задаётся выражением ((w → z) ∧ (¬ x → y)) → ((y ≡ w) ∨ (z ∧ ¬ x)). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Вопрос 3
Для кодирования некоторой последовательности, состоящей из букв Е, Л, П, К, Р, C решили использовать неравномерный двоичный код, для которого выполняется условие Фано. Для букв К и Р использовали соответственно кодовые слова 011, 11. Найдите кодовую последовательность наименьшей длины для кодирования слова ПЕРЕПЕЛ и запишите полученный результат в восьмеричном коде. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Вопрос 4
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К полученной записи дописываются разряды. Если в числе четное количество единиц, слева дописывается 1 и справа два нуля, если нечетное – слева дописываются две единицы.
3) Результат переводится в десятичную систему и выводится на экран.
Пример. Дано число N = 13. Алгоритм работает следующим образом:
1. Двоичная запись числа N: 1101.
2.Число единиц нечетное, следовательно слева дописываем две единицы слева – 11 + 1101 = 111101.
3. На экран выводится число 61 = 1111012.
Для какого наименьшего значения N результат работы автомата – число, не меньшее 412?
Вопрос 5
Для хранения сжатого аудио файла с заголовком отведено 25 Мбайт памяти. Известно, что фрагмент кодируется в формате стерео, частотой дискретизации 50 кГц и глубиной кодирования 16 бит. После кодирования звуковых дорожек фрагмент сжимается. Сжатый размер закодированного фрагмента меньше исходного на 25%. К сжатому фрагменту дописывается информация о заголовке и дополнительная информация, суммарно занимающая 40 Кбайт. Запишите в ответе целое число - максимальную длительность в минутах фрагмента, который сохраняется по приведенному алгоритму?
Вопрос 6
Ваня составляет 6-буквенные слова из букв В, И, Д, Е, О. Его интересуют коды, в которых есть хотя бы одна буква И и хотя бы одна буква Е. Кроме того, все гласные в слове должны стоять в алфавитном порядке. Сколько различных подходящих кодов может составить Ваня?
Вопрос 7
При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 252 символов и содержащий только десятичные цифры и символы из 1700-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 4096 идентификаторов. В ответе запишите только целое число – количество Кбайт.
Вопрос 8
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует маршрутов, начинающихся и оканчивающихся в пункте Г, не проходящих дважды через один и тот же пункт и не проходящих через город Б?
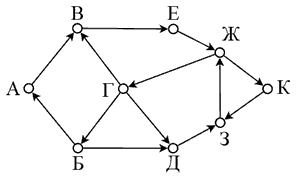
Вопрос 9
Операнды арифметического выражения записаны в системах счисления с основаниями 15 и 17.
123x515 + 67y917
В записи чисел переменными x и y обозначены неизвестные цифры из алфавитов 15-ричной и 17-ричной систем счисления соответственно. Определите значения x, y, при которых значение данного арифметического выражения кратно 131. Для найденных значений x, y вычислите частное от деления значения арифметического выражения на 131 и укажите его в ответе в десятичной системе счисления. Если можно выбрать x, y не единственным образом, возьмите ту пару, в которой значение y меньше. Основание системы счисления в ответе указывать не нужно.
Получите комплекты видеоуроков + онлайн версии
 0
0 1286
1286 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








