2 задача ЕГЭ часть 2 (+ повторение задач 5, 12, 16, 23)

Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.

На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

Логическая функция F задаётся выражением ¬x ∧ y ∧ z ∨ x ∧ ¬y ∧ ¬w.

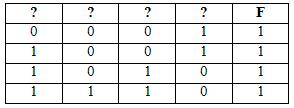
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

Логическая функция F задаётся выражением (¬x ∧ z) ∨ (¬x ∧ ¬y ∧ ¬z).

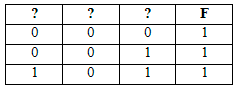
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

Логическая функция F задаётся выражением a ∧ ¬b ∨ (a ∨ b) ∧ c ∨ d. На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.

В ответе напишите буквы a, b, c, d в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Логическая функция F задаётся выражением ¬x ∧ y ∨ z ∧ ¬y ∨ ¬z ∧ w. На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Логическая функция F задаётся выражением ((z → y) ∧ (¬ x → w)) → ((z ≡ w) ∨ (y ∧ ¬ x)). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Логическая функция F задаётся выражением (a → b) ∧ ¬(b ≡ c) ∧ (d → a). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.

В ответе напишите буквы a, b, c, d в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Логическая функция F задаётся выражением (y → x ∨ z) ∧ (z → y).

На рисунке приведён фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Примечание. Да, в формуле нет переменной w. Но тут все правильно и задача имеет единственное решение.

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1. Строится шестнадцатеричная запись числа.

2. Далее, эта запись обрабатывается по следующему правилу:

а) Если цифр B в ней чётное количество, то к этой записи слева дописывается 1.

б) Если цифр B в ней нечётное количество, то к этой записи справа дописывается 1.

Полученная таким образом запись является шестнадцатеричной записью искомого числа R.

Например, возьмём число 91. Строим шестнадцатеричную запись числа: 5B. Цифра B в нём одна – нечётное количество, значит, единицу дописываем справа. Итоговое число 5B1 переводим в десятичную систему – 1457. Число 1457 и является результатом работы алгоритма.

Определите количество натуральных чисел N, для которых результатом выполнения алгоритма может стать двухзначное число.

На вход алгоритма подаётся натуральное число N.

Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. Далее эта запись обрабатывается по следующему правилу:

а) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10;

б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11.

Полученная таким образом запись является двоичной записью искомого числа R.

Например, для исходного числа 6₁₀ = 110₂ результатом является число 1000₂ = 8₁₀, а для исходного числа 4₁₀ = 100₂ результатом является число 1101₂ = 13₁₀. Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, не меньшее, чем 16.

В ответе запишите это число в десятичной системе счисления

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.

1. заменить (v, w)

2. нашлось (v)

Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.

Дана программа для исполнителя Редактор:

На вход приведённой программы поступает строка, состоящая из 1 и следующими за ней n нулями(n - натуральное число). Определите, сколько существует значений n от 1 до 100, для которых длина получившейся строки делится на 7.

Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 55 двоек, 44 троек и 33 единиц, идущих друг за другом? В ответе запишите полученную строку. 

Примечание: команда "ЗАМЕНИТЬ С КОНЦА СТРОКИ(v, w)" заменяет в строке первое СПРАВА вхождение элемента v на w.

НАЧАЛО

ПОКА нашлось (222) ИЛИ нашлось (333) ИЛИ нашлось (111) 

ЕСЛИ нашлось (222)  

    ТО заменить (222, 11)

   ЕСЛИ нашлось (222)

      ТО заменить С КОНЦА СТРОКИ (222, 11)

ИНАЧЕ ЕСЛИ нашлось (111)

    ТО заменить (111, 3)

ИНАЧЕ заменить (333, 1)

КОНЕЦ ЕСЛИ 

КОНЕЦ ПОКА 

КОНЕЦ 

Функция F(x, y) задается рекуррентным соотношением:

F(x, 0) = x

F(x, y) = F(y, x mod y)

Для скольких чисел X в диапазоне [1:1000] функция F(x, 48) будет равна 1?

Примечание: mod означает операцию остатка от деления

Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1

2. Умножить на 2

Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя – это последовательность команд. Например, если в начальный момент на экране находится число 1, то программа 212 последовательно преобразует его в 2, 3, 6.

Сколько существует программ, которые преобразуют исходное число 1 в число 16, и при этом никакая команда не повторяется более двух раз подряд?

Исполнитель преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера:

1. Прибавить 1

2. Прибавить 2

3. Умножить на 2

Первая команда увеличивает число на 1, вторая – на 2, третья – вдвое.

Программа для исполнителя – это последовательность команд.

Сколько существует таких программ, которые исходное число 3 преобразуют в число 25 и при этом в программе есть все три команды?