Тренировочные задания № 7
1. Функция y=f(x) определена на промежутке (-5;5). На рис.1 изображён график производной этой функции. Найдите количество точек графика функции , в которых касательная наклонена под углом 120О к положительному направлению оси абсцисс.
2. Функция у = f(х) определена на промежутке (—5; 5). На рисунке 2 изображён график производной этой функции. Найдите количество точек графика функции, в которых касательные наклонены под углом 150° к положительному направлению оси абсцисс.
3. Функция у = f(х) определена на промежутке (—5; 5). На рисунке 3 изображён график производной этой функции. К графику функции у= f(х) провели касательные во всех точках, абсциссы которых — положительные целые числа. Укажите количество точек графика функции у = f(х), в которых проведённые касательные имеют отрицательный угловой коэффициент.
4. Найдите угловой коэффициент касательной, проведённой к графику функции у = f(х) в точке с абсциссой хо = 4, если на рисунке 4 изображён график производной этой функции.
5. Найдите тангенс угла наклона касательной, проведённой к графику функции f(х) = 5х2 — 7х + 2 в точке с абсциссой хо = 2.
6. Функция у = f(х) определена на промежутке (—5; 4). На рис. 5 изображён график её производной. Найдите число касательных к графику функции у = f(х), которые наклонены под углом в 45° к положительному направлению оси абсцисс.
7. Функция у = f(х) определена на промежутке (-4; 5). На рисунке 6 изображён график её производной. Найдите угол наклона (в градусах) касательной к графику функции у = f(х) в точке х = 1 к положительному направлению оси Ох.
8. В точке А графика функции у = —х2 + 4х +11 проведена касательная к нему, параллельная прямой у = 1 — 2х. Найдите сумму координат точки А
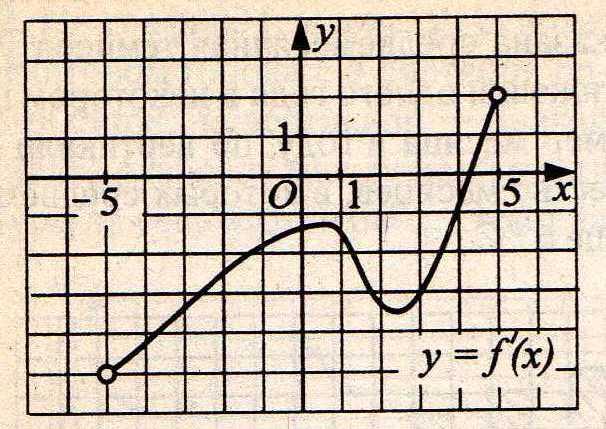 Рис1
Рис1
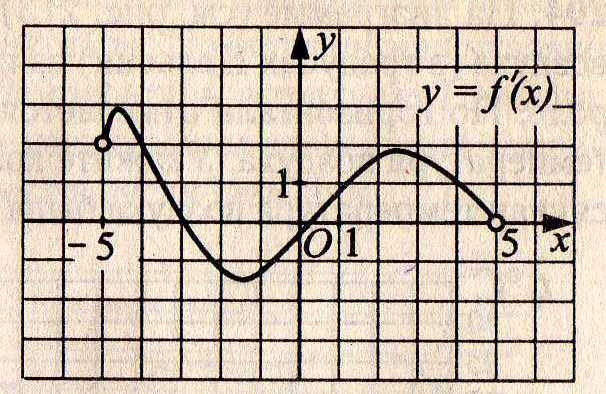 Рис.2
Рис.2
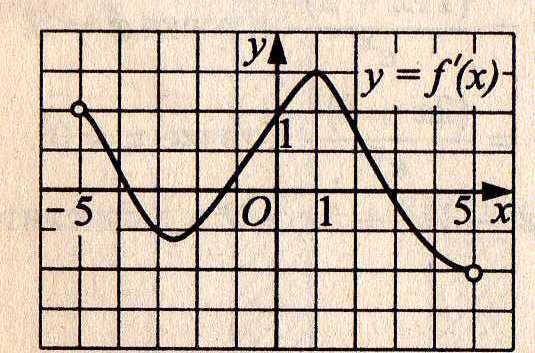 Рис.3
Рис.3
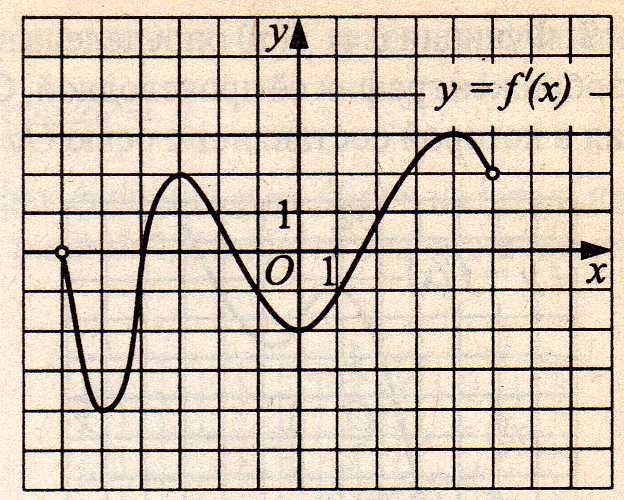 Рис.4
Рис.4
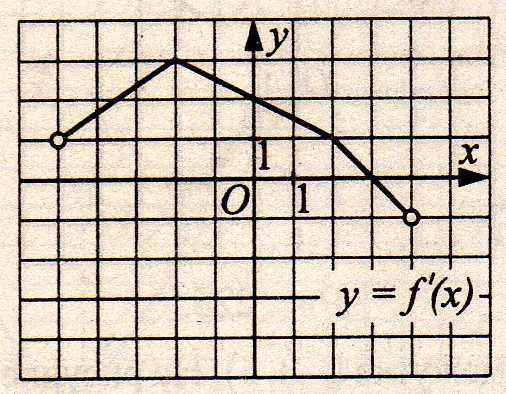 Рис.5
Рис.5
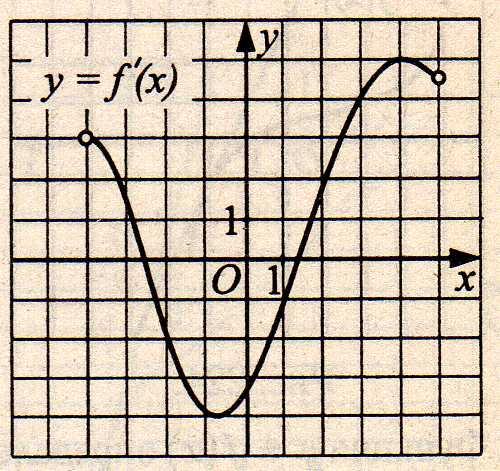 Рис.6
Рис.6
9. На рисунке 7 изображены график функции у = f(х) и касательная к нему в точке (2; —1). Найдите значение производной этой функции при х=2.
10. На рисунке 8 изображены график функции f(х) и касательная к этому графику, проведённая в точке с абсциссой хo . Найдите значение производной f(х) в точке хo .
11. На рисунке 9 изображен график функции у = f(х). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 5. Найдите f 1(5).
12. На рисунке 10 изображен график производной функции f(х). Найдите абсциссу точки, в которой касательная к графику у = f(х) параллельна прямой у = 1 или совпадает с ней.
13. На рисунке 11 изображён график функции у = f(х), определённой на промежутке [- 8; 7]. Найдите количество точек, в которых касательная к графику функции параллельна прямой у = - 15.
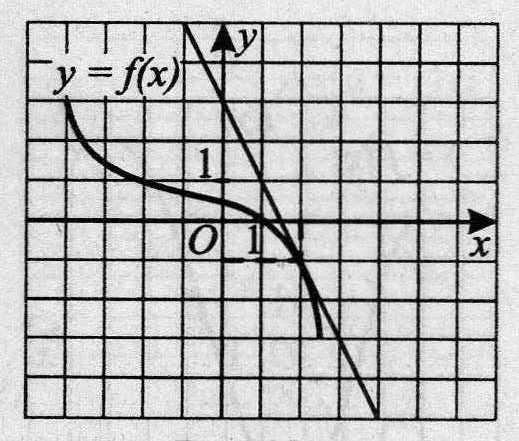 Рис.7
Рис.7
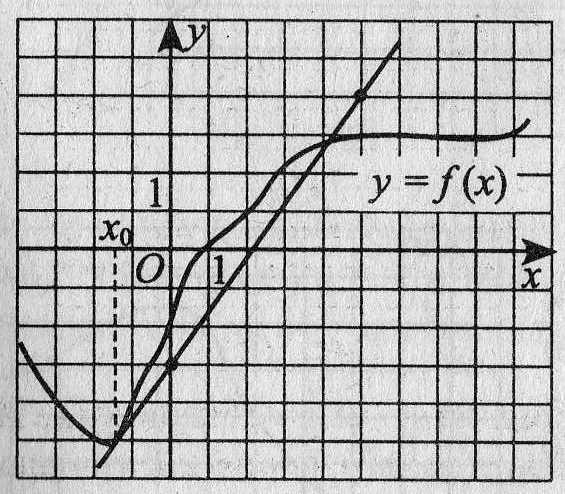 Рис.8
Рис.8
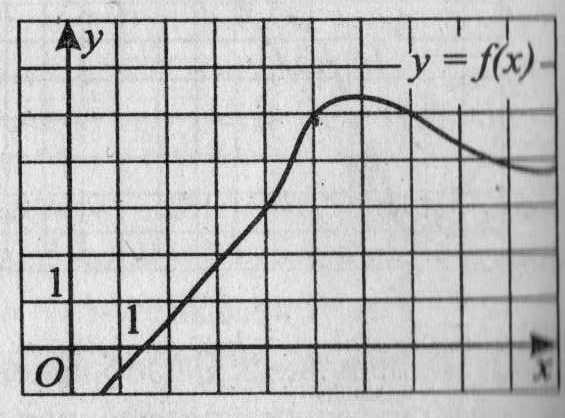 Рис.9
Рис.9
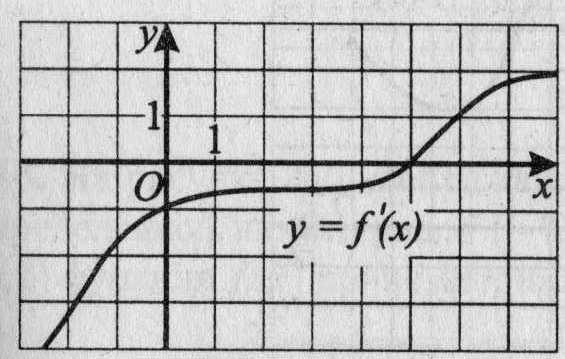 Рис.10
Рис.10
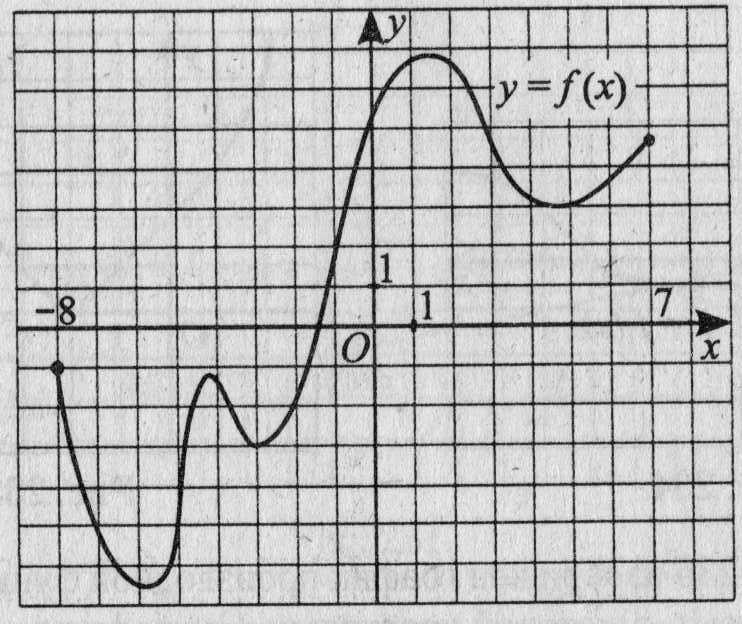 Рис.11
Рис.11
14. На рисунке 12 изображён график производной функции у = f(х), определённой на интервале (-8; 7). В какой точке отрезка [-7; -3] функция f(х) принимает наименьшее значение?
15. На рисунке 13 изображён график производной функции у = f(х), определённой на интервале (-7; 7). Определите, в какой точке отрезка [2; 6] функция f(х) принимает наибольшее значение.
16. На рисунке 14 изображён график производной функции у = f(х), определённой на интервале (-7; 7). Найдите точку экстремума функции f(х) на интервале (-1; 5).
17. На рисунке 15 изображён график производной функции у = f(х), определённой на интервале (-8; 8). Найдите количество точек, в которых касательная к графику функции f(х) параллельна прямой у = -Зx + 5 или совпадает с ней.
18. На рисунке 16 изображён график функции у = f(х), определённой на промежутке [-6; 6]. Определите количество целых точек, в которых производная функции f(х) отрицательна.
19. На рисунке 17 изображён график производной функции у = f(х), определённой на интервале (-7; 7). Найдите количество точек максимума функции f(x) на интервале (-6; 5).
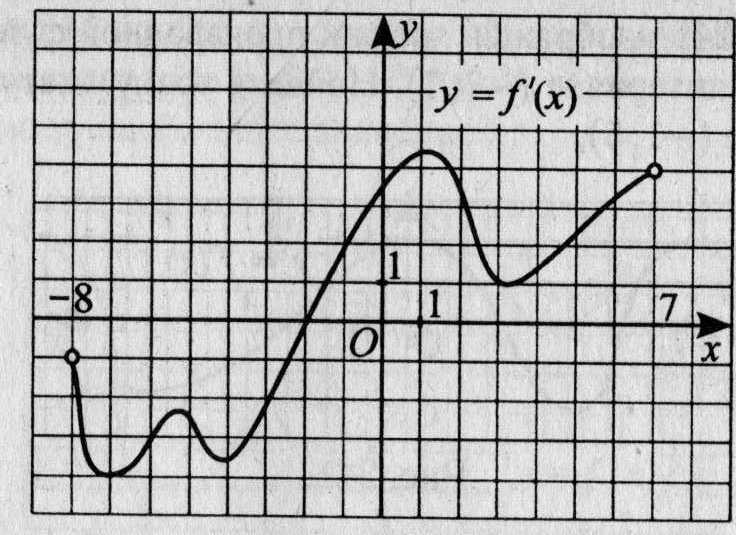 Рис.12
Рис.12
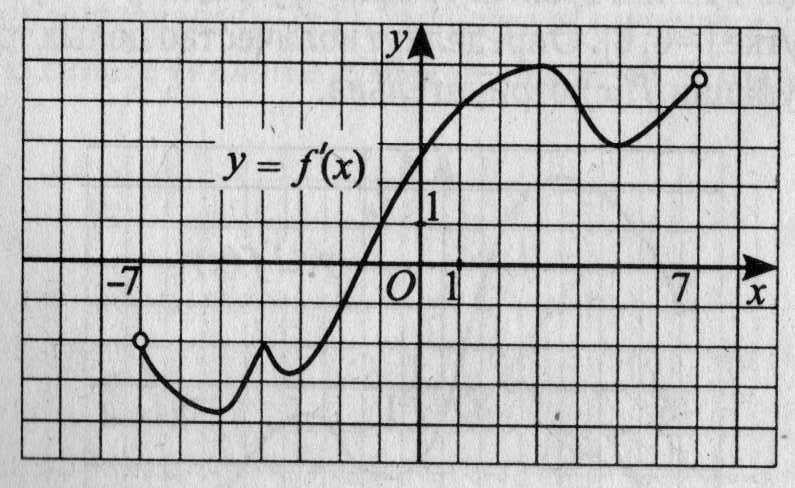 Рис.13
Рис.13
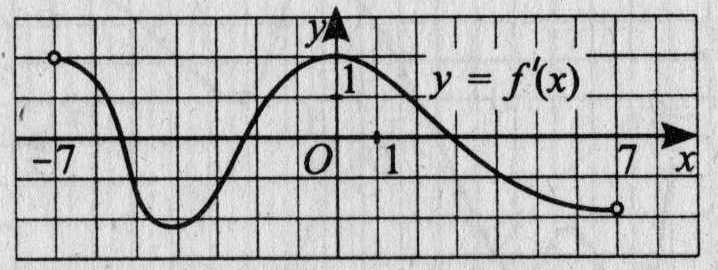 Рис.14
Рис.14
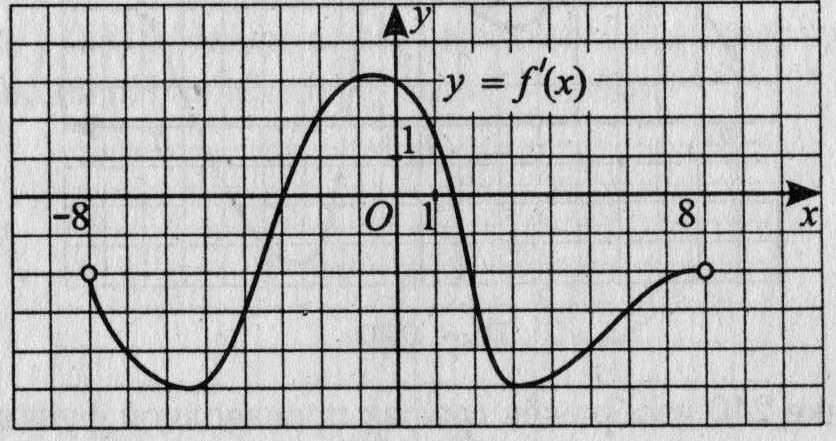 Рис.15
Рис.15
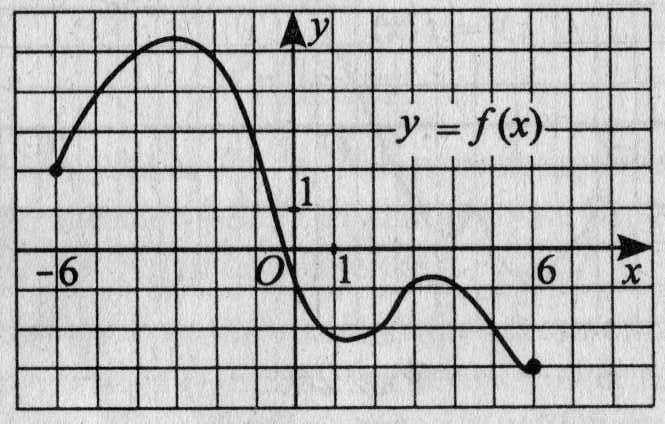 Рис.16
Рис.16
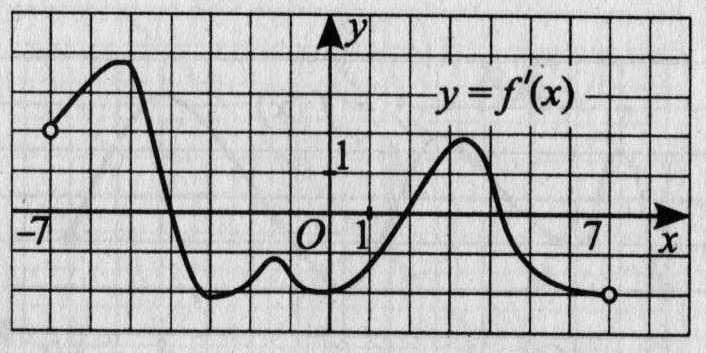 Рис.17
Рис.17
20. На рисунке 18 изображён график производной функции у =f(х), определённой на интервале (-7; 7). Найдите промежутки убывания функции y= f(x). В ответе укажите сумму абсцисс целых точек, входящих в эти промежутки.
21. Прямая у = 9х + 5 является касательной к графику функции
у = —х2 + Ьх — 11. Найдите Ь, учитывая, что абсцисса точки касания
больше 1.
22. Прямая у = Зх + 30 параллельна касательной к графику функции у = х3 + 5х2 — 5х — 18. Найдите наименьшую из возможных абсцисс точек касания.
23. На рисунке 19 изображён график функции у = f(x) и касательная к этому графику в точке xо. Уравнение касательной у = 2x - 6. Найдите
значение производной функции у = -0,5 f(x) + 7 в точке xo.
24. На рисунке 20 изображён график производной функции у =f(х), определённой на интервале (-9; 4). В какой точке отрезка [-6; 3] функция f(х) принимает наименьшее значение?
25. Точка движется по координатной прямой согласно закону
x (t) = 1,5t2 -3t + 7, где x(t) — координата в момент времени t. В какой
момент времени скорость точки будет равна 12?
26. Ребёнок на санках в первые 4 с движения с горки проезжал расстояние, заданное формулой s(t) = 0,5t 3 + 2t . Найдите его ускорение в момент
времени t = 3.
27. На рисунке 21 представлены график движения тела и касательная к графику в момент времени t = 5. Определите по графику скорость движения тела (в км/ч) в этот момент времени.
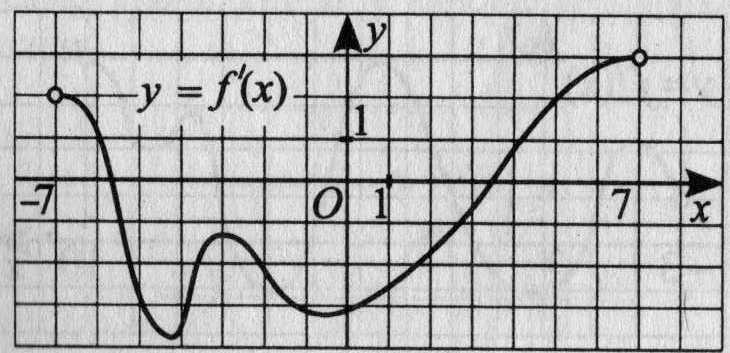 Рис.18
Рис.18
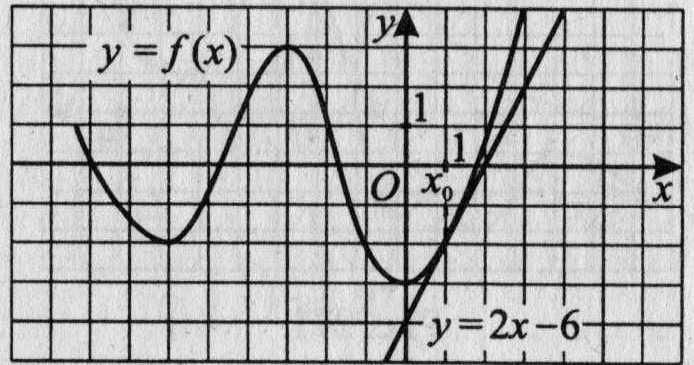 Рис.19
Рис.19
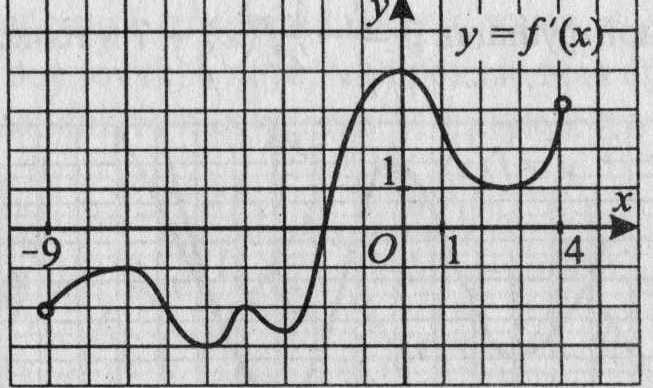 Рис.20
Рис.20
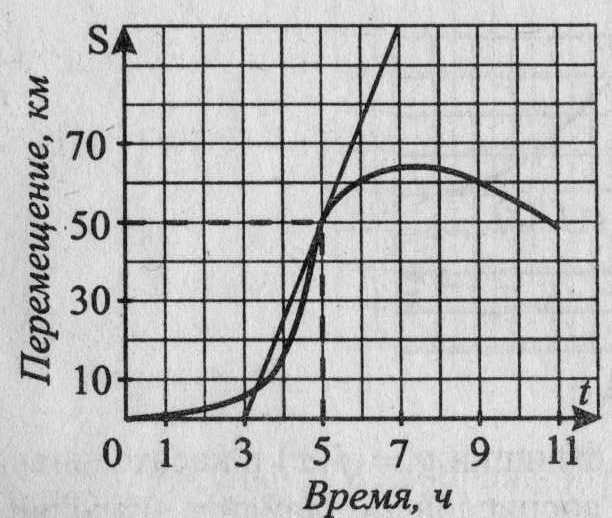 Рис.21
Рис.21
28. На рисунке 22 представлены график движения тела и касательная к графику в момент времени t = 8. Определите по графику скорость движения тела (в км/ч) в этот момент времени.
29. На рисунке 23 изображена зависимость скорости некоторой материальной точки от времени. На оси абсцисс откладывается время t в секундах, на оси ординат — скорость v в метрах в секунду. Определите, сколько раз за время движения ускорение точки обращалось в нуль (начало и конец движения не учитывайте).
30. При метании бумеранга его скорость изменялась по формуле
v(t) = 9t — t2 в метрах в секунду. Найдите расстояние, которое преодолел
бумеранг, если он был в движении 9 секунд. (Ответ укажите в метрах.)
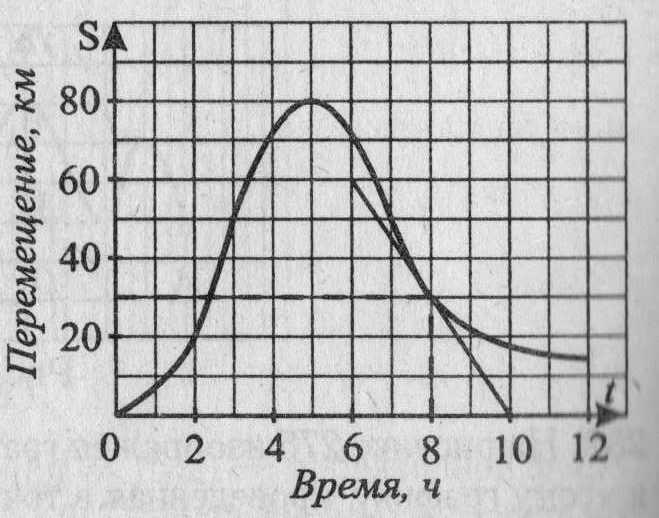 Рис.22
Рис.22
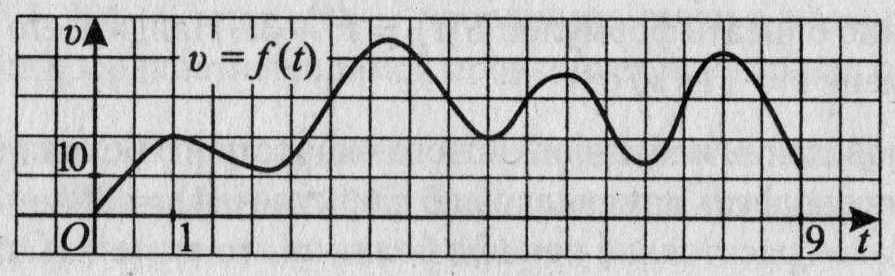 Рис.23
Рис.23
| № | ответ | № | ответ | № | ответ |
| 1 | 3 | 11 | 1 | 21 | 17 |
| 2 | 2 | 12 | 5 | 22 | - 4 |
| 3 | 2 | 13 | 5 | 23 | - 1 |
| 4 | 3 | 14 | - 3 | 24 | - 2 |
| 5 | 13 | 15 | 6 | 25 | 5 |
| 6 | 1 | 16 | 3 | 26 | 9 |
| 7 | 135 | 17 | 4 | 27 | 25 |
| 8 | 17 | 18 | 6 | 28 | 15 |
| 9 | - 2 | 19 | 2 | 29 | 7 |
| 10 | 1,4 | 20 | - 9 | 30 | 121,5 |
|
|
|
|
|
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход












 Тренировочные задания №7 по подготовке к ЕГЭ (профильный уровень) (1.08 MB)
Тренировочные задания №7 по подготовке к ЕГЭ (профильный уровень) (1.08 MB)
 0
0 888
888 14
14 Нравится
0
Нравится
0


