Тест «Основные фигуры пространства. Аксиомы стереометрии» в среде MS Power Point

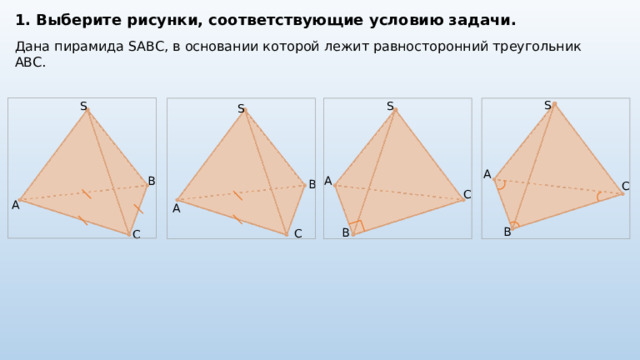
1. Выберите рисунки, соответствующие условию задачи.

Дана пирамида SABC, в основании которой лежит равносторонний треугольник ABC.

S

S

S

S

A

B

A

B

C

C

А

A

B

B

C

С

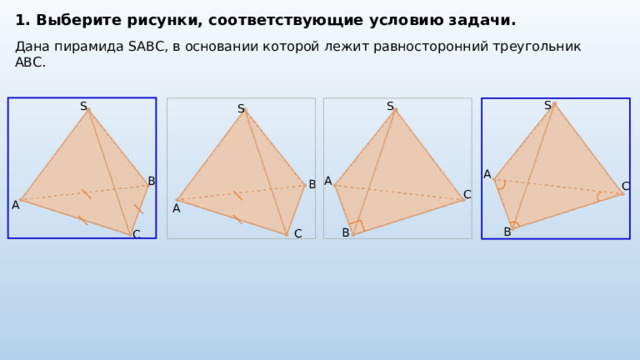
1. Выберите рисунки, соответствующие условию задачи.

Дана пирамида SABC, в основании которой лежит равносторонний треугольник ABC.

S

S

S

S

A

A

B

B

C

C

А

A

B

B

C

С

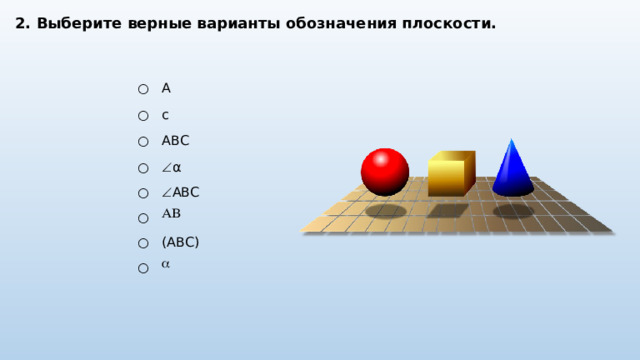
2. Выберите верные варианты обозначения плоскости.

○

A

○

c

○

ABC

○

○

 α

 ABC

○

AB

○

(ABC)

○



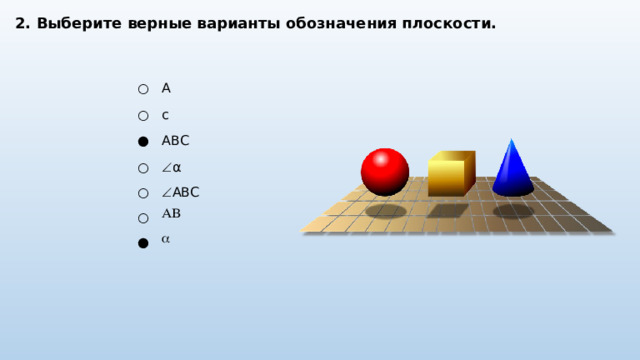
2. Выберите верные варианты обозначения плоскости.

○

A

○

c

●

ABC

○

 α

○

 ABC

○

AB

●



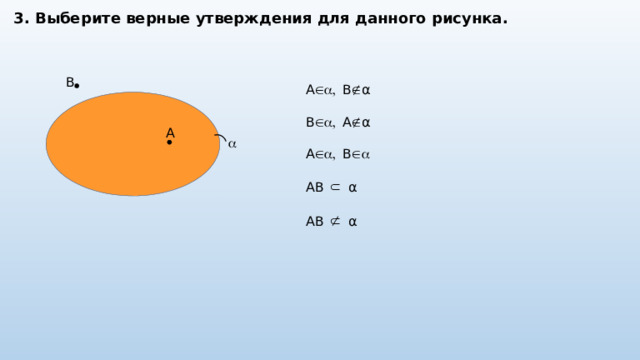
3. Выберите верные утверждения для данного рисунка.

B

A , B  α

B , A  α

A , B 

AB  α

AB  α

A



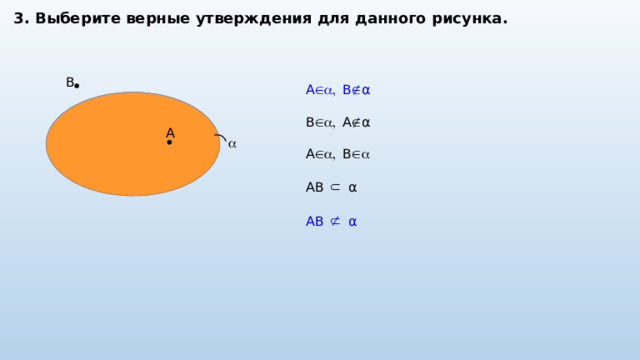
3. Выберите верные утверждения для данного рисунка.

B

A , B  α

B , A  α

A , B 

AB  α

AB  α

A



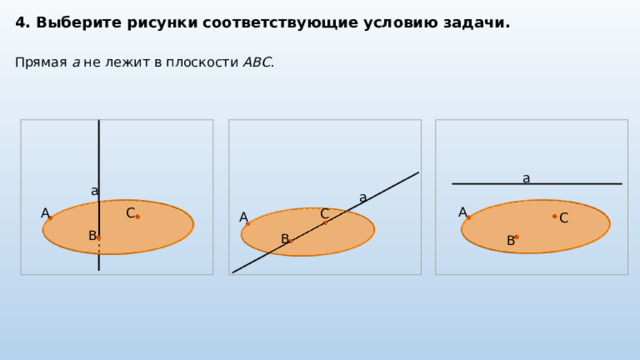
4. Выберите рисунки соответствующие условию задачи.

Прямая a не лежит в плоскости ABC .

a

a

a

A

A

C

C

A

C

B

B

B

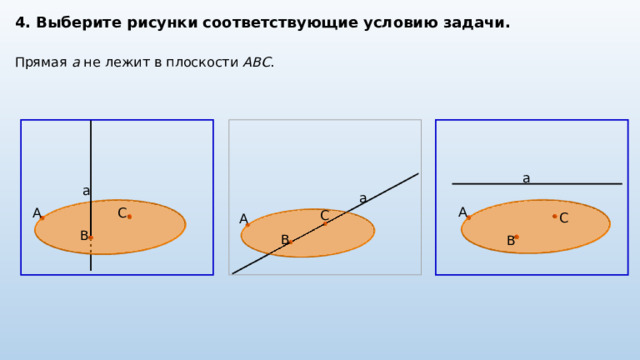
4. Выберите рисунки соответствующие условию задачи.

Прямая a не лежит в плоскости ABC .

a

a

a

A

A

C

C

C

A

B

B

B

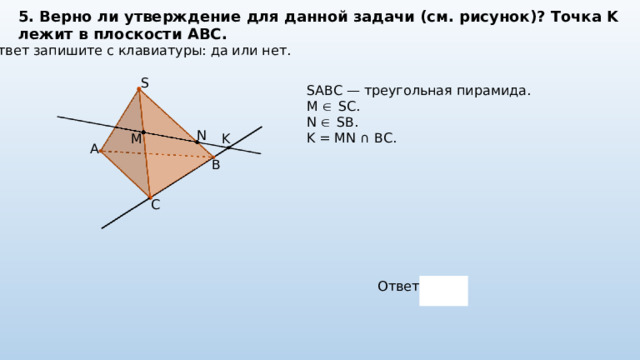
5. Верно ли утверждение для данной задачи (см. рисунок)? Точка K лежит в плоскости ABC.

Ответ запишите с клавиатуры: да или нет.

S

SABC — треугольная пирамида.

M  SC.

N  SB.

K = MN ∩ BC.

N

K

M

A

B

C

Ответ:

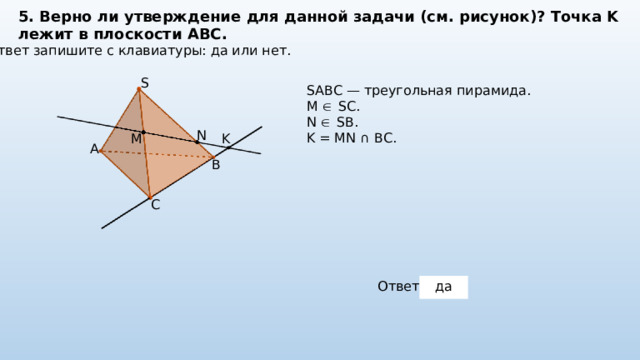
5. Верно ли утверждение для данной задачи (см. рисунок)? Точка K лежит в плоскости ABC.

Ответ запишите с клавиатуры: да или нет.

S

SABC — треугольная пирамида.

M  SC.

N  SB.

K = MN ∩ BC.

N

K

M

A

B

C

Ответ:

да

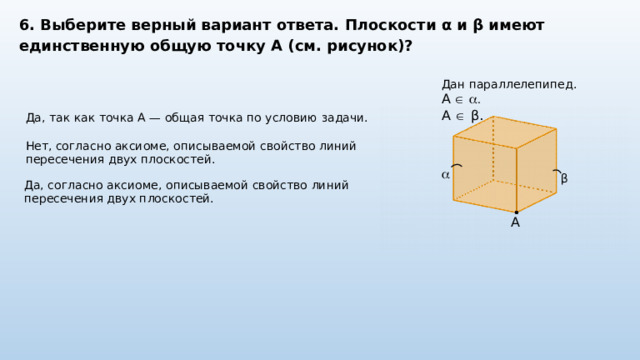
6. Выберите верный вариант ответа. Плоскости α и β имеют единственную общую точку A (см. рисунок)?

Дан параллелепипед.

A  .

A  β.

Да, так как точка A — общая точка по условию задачи.

Нет, согласно аксиоме, описываемой свойство линий пересечения двух плоскостей.



β

Да, согласно аксиоме, описываемой свойство линий пересечения двух плоскостей.

A

Если три прямые попарно пересекаются, то они либо лежат в одной плоскости, либо имеют одну общую точку.

6. Выберите верный вариант ответа. Плоскости α и β имеют единственную общую точку A (см. рисунок)?

Дан параллелепипед.

A  .

A  β.

Да, так как точка A — общая точка по условию задачи.

Нет, согласно аксиоме, описываемой свойство линий пересечения двух плоскостей.



β

Да, согласно аксиоме, описываемой свойство линий пересечения двух плоскостей.

A

Если три прямые попарно пересекаются, то они либо лежат в одной плоскости, либо имеют одну общую точку.

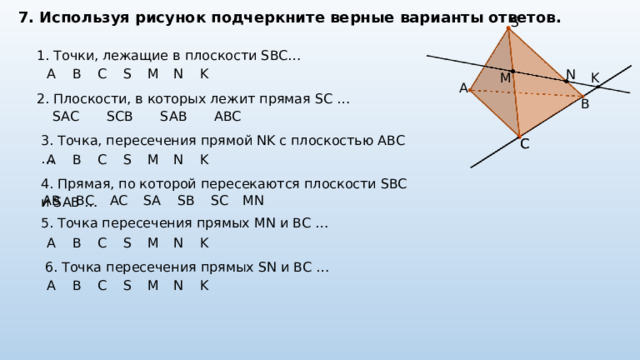
7. Используя рисунок подчеркните верные варианты ответов.

S

1. Точки, лежащие в плоскости SBC…

N

A

B

C

S

M

N

K

K

M

A

2. Плоскости, в которых лежит прямая SC …

B

SAC

SCB

SAB

ABC

3. Точка, пересечения прямой NK с плоскостью ABC …

C

C

A

B

C

S

M

N

K

4. Прямая, по которой пересекаются плоскости SBC и SAB …

AB

BC

AC

SA

SB

SC

MN

5. Точка пересечения прямых MN и BC …

A

B

C

S

M

N

K

6. Точка пересечения прямых SN и BC …

A

B

C

S

M

N

K

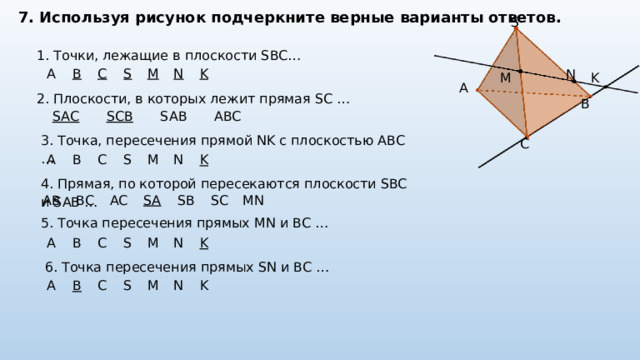
7. Используя рисунок подчеркните верные варианты ответов.

S

1. Точки, лежащие в плоскости SBC…

N

A

B

C

S

M

N

K

K

M

A

2. Плоскости, в которых лежит прямая SC …

B

SAC

SCB

SAB

ABC

3. Точка, пересечения прямой NK с плоскостью ABC …

C

A

B

C

S

M

N

K

4. Прямая, по которой пересекаются плоскости SBC и SAB …

AB

BC

AC

SA

SB

SC

MN

5. Точка пересечения прямых MN и BC …

A

B

C

S

M

N

K

6. Точка пересечения прямых SN и BC …

A

B

C

S

M

N

K

8. Выделите верные утверждения синим цветом, неверные – красным.

Через любые две точки проходит единственная прямая.

Любые три точки лежат в одной плоскости.

Если три прямые попарно пересекаются, то они лежат в одной плоскости.

Через любые три точки, не лежащие на одной прямой, проходит плоскость, притом только одна.

Если три прямые попарно пересекаются, то они имеют одну общую точку пересечения.

Если три прямые попарно пересекаются, то они либо лежат в одной плоскости, либо имеют одну общую точку.

8. Выделите верные утверждения синим цветом, неверные – красным.

Через любые две точки проходит единственная прямая.

Любые три точки лежат в одной плоскости.

Если три прямые попарно пересекаются, то они лежат в одной плоскости.

Через любые три точки, не лежащие на одной прямой, проходит плоскость, притом только одна.

Если три прямые попарно пересекаются, то они имеют одну общую точку пересечения.

Если три прямые попарно пересекаются, то они либо лежат в одной плоскости, либо имеют общую точку.

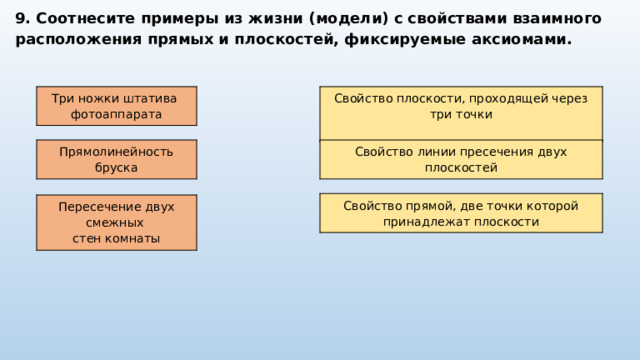
9. Соотнесите примеры из жизни (модели) с свойствами взаимного расположения прямых и плоскостей, фиксируемые аксиомами.

Три ножки штатива

Свойство плоскости, проходящей через три точки

фотоаппарата

Прямолинейность бруска

Свойство линии пресечения двух плоскостей

Свойство прямой, две точки которой принадлежат плоскости

Пересечение двух смежных

стен комнаты

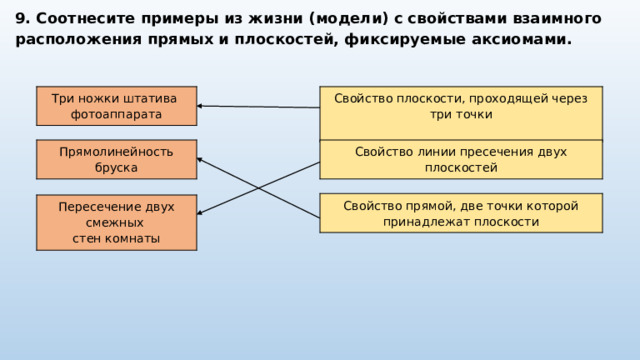
9. Соотнесите примеры из жизни (модели) с свойствами взаимного расположения прямых и плоскостей, фиксируемые аксиомами.

Три ножки штатива

Свойство плоскости, проходящей через три точки

фотоаппарата

Прямолинейность бруска

Свойство линии пресечения двух плоскостей

Свойство прямой, две точки которой принадлежат плоскости

Пересечение двух смежных

стен комнаты

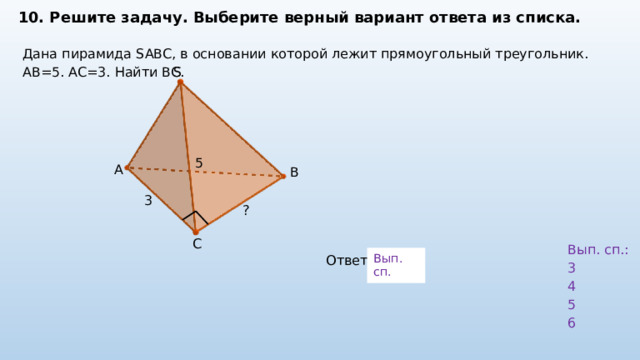
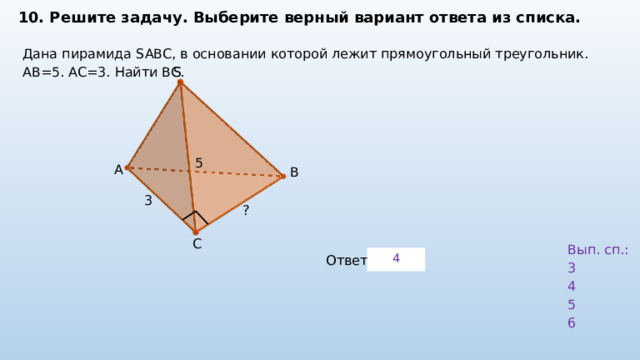
10. Решите задачу. Выберите верный вариант ответа из списка.

Дана пирамида SABC, в основании которой лежит прямоугольный треугольник. AB=5. AC=3. Найти ВС.

S

5

A

B

3

?

C

Вып. сп.:

3

4

5

6

Вып. сп.

Ответ:

10. Решите задачу. Выберите верный вариант ответа из списка.

Дана пирамида SABC, в основании которой лежит прямоугольный треугольник. AB=5. AC=3. Найти ВС.

S

5

A

B

3

?

C

Вып. сп.:

3

4

5

6

4

Ответ: