Решение задач по теме ускорение 1 курс спо

Решение задач по теме : ускорение

Цель: закрепить знания об ускорении и движении с постоянным ускорением путём решения задач.

Разминка.

По два веселых вопроса:

1. Варит отлично твоя голова: пять плюс один получается… (не два, а шесть)

2. Вышел зайчик погулять, лап у зайца ровно… (не пять, а четыре)

3. Ходит в народе такая молва: шесть минус три получается… (не два, а три)

4. Говорил учитель Ире, что два больше, чем… (один, а не четыре)

5. Меньше в десять раз, чем метр, всем известно… (дециметр)

6. Ты на птичку посмотри: лап у птицы ровно … (две, а не три)

7. У меня собачка есть, у нее хвостов аж… (один, а не шесть)

8. У доски ты говори, что концов у палки… (два, а не три)

9. Отличник тетрадкой своею гордится: внизу, под диктантом, стоит… (не единица, а пять)

10. На уроках будешь спать, за ответ получишь… (два, а не пять)

11. Вот пять ягодок в траве. Съел одну, осталось -… (не две, а четыре)

12. Мышь считает дырки в сыре: три плюс две – всего… (пять, а не четыре).

Опорное повторение:

Вспомним формулы необходимые для практической части нашего урока.

1.Формула площади треугольника

2.Формула площади прямоугольника

3.Формула ускорения

4.Квадратное уравнение

5.Уравнение координаты

1. Практическое задание:

Теперь приступим к практическому заданию.

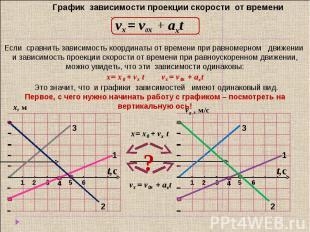
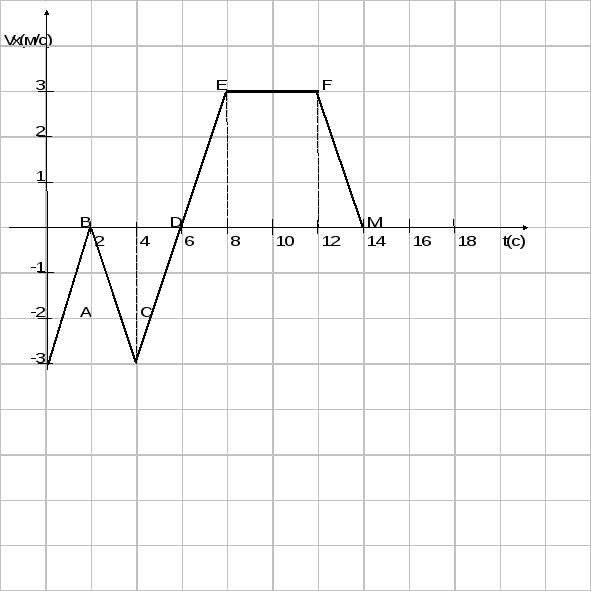
Итак, на рисунке изображен график зависимости проекции скорости от времени движения. Постройте график зависимости координаты от времени, если начальная координата тела х0 = 5 м. Определите ускорение тела по модулю и путь пройденный телом за все время движения.

1. Задание

Дайте характеристику движения тела на каждом участке графика.

Ответ:

АВ – равнозамедленно

СД – равнозамедленно

ЕФ – равномерно

ВС – равноускоренно

ДЕ – равноускоренно

ФМ – равнозамедленно

1. Задание

Чему равно ускорение тела по модулю?

Ответ: Ускорение на всех участках графика (кроме ЕФ) равно а=1,5 м/с². На участке ЕФ ускорение равно нулю, так как скорость тела не изменялась в течение 4 с.

1. Задание

Определите координаты тела через каждые 2 секунды.

Ответ:

1.Первые 2 секунды тело двигалось равнозамедленно противоположно оси Х. Изменение координаты тела численно равно площади треугольника АОВ.

Δх1=1/2*2(-3)=-6/2=-3 м

Поэтому координата в конце 2-й секунды будет равна:

Х1 = х0+Δх1; х1=5-3=2м х1=2м

Графиком координаты на этом отрезке времени является ветвь параболы А1В1, где точка В1 – вершина этой параболы

2.В следующие 2 секунды тело двигалось равноускоренно, но в том же направлении, что и в начале. Изменение координаты за этот интервал времени будет таким же что и в первом участке движения:

Δх2=1/2*2(-3)=-6/2=-3

А координата к концу 4 секунды будет:

Х2= х1+ Δх2; х2=2 -3=-1м х2=-1м

Графиком координаты на данном интервале времени является ветвь параболы В1С1.

3.В интервале времени от 4-й до 6-й секунды тело двигалось равнозамедленно и в прежнем направлении, поэтому

Δх3=1/2*2(-3)=-6/2=-3

А координата тела к концу 6-й секунды будет:

Х3= х2+ Δх3; х3=-1 -3=-4м х3=-4м

Графиком координаты на интервале времени от 4 до 6 с представляется парабола С1Д1, где Д1- вершина параболы

4.С 6-й с до 8-й с тело двигалось равноускоренно в положительном направлении оси Х. Изменение координаты за этот интервал времени будет:

Δх4=1/2*2*3=6/2=3 м

Координата тела к концу 8-й секунды будет:

Х4= х3+ Δх4; х4=-4+3=-1м х4=-1м

Графиком координаты на этом отрезке времени является ветвь параболы Д1Е1.

5.На отрезке времени от 8 с до 12 с тело двигалось с постоянной скоростью 3 м/с в течении 4 с. Изменение координаты за этот промежуток времени будет:

Δх5=3*4=12 м

Тогда координата тела к концу 12-й секунды будет:

Х5=х4+ Δх5; х5=-1+12=11м х5=11 м

График – прямая Е1Ф1 – движение равномерное.

6. И на последнем отрезке времени движение было равнозамедленным в том же положительном направлении. Изменение координаты за последние 2 с будет:

Δх6=1/2*2*3=6/2=3 м

Тогда координата тела к концу 14-й секунды будет:

Х6=х5+ Δх6; х6=11+3=14м х6=14 м

График – парабола Ф1М1

1. Задание

По точкам постройте график зависимости координаты тела от времени.

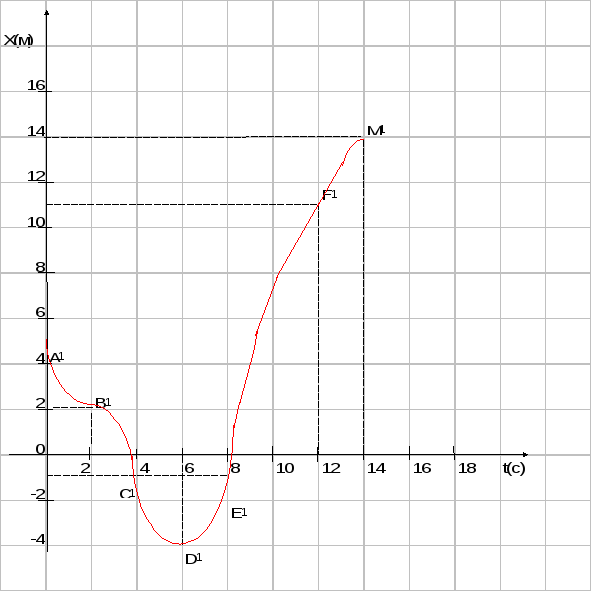
1. Задание

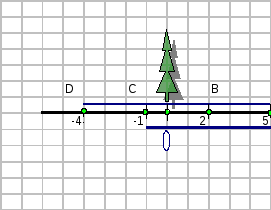
Указать положение тела на дороге.

Ответ: направим ось х вдоль дороги, за начало отсчета выберем дерево, или можно столб.

1. Задание

Определить путь, пройденный телом за 14 с. движения. Рассмотрим площади фигур, ограниченных графиком скорости.

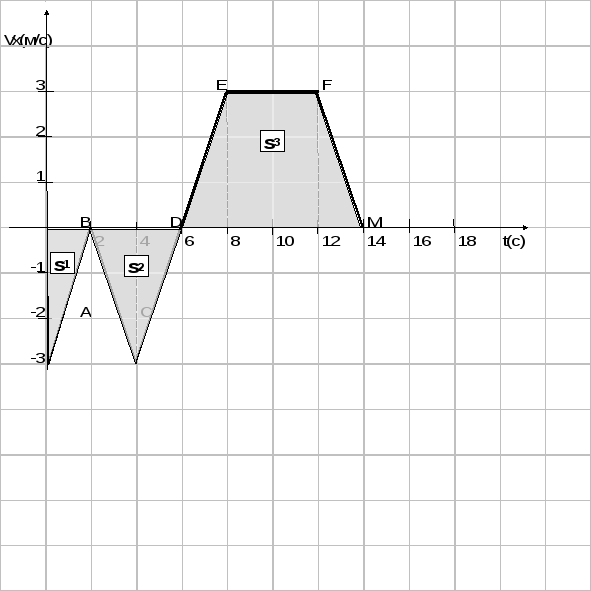
s1=1/2*2*3=6/2=3 м (треугольник)

s2=1/2*4*3=12/2=6 м (треугольник)

s3=(4+8)/2*3=12/2*3=6*3=18 м (трапеция)

s общ=s1+s2+s3=3+6+18=27 м

ответ: 27 м