Абитуриент, проверь себя!
(характерные ошибки и разбор методов решения),
На вступительных экзаменах по математике встречаются задания, в которых требуется решить уравнение. К решению уравнений в конечном итоге сводится многие геометрические и текстовые задачи. Процесс решения уравнения, как правило, состоит в последовательной замене сложного уравнения более простым или в замене совокупностью уравнений (неравенств, систем). Основной источник ошибок при решений уравнений – это потеря корней и появление новых корней, не являющихся решением исходного уравнения.
1.Иррациональные уравнения:
Пример1. Решить уравнение 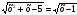
Решение. Возведем обе части данного уравнения в квадрат. Получим уравнение х2+х – 5 = х-1 или х2-4 = 0. Находим корни х 1 = 2 и х 2 = -2. Подставляя решение в исходное уравнение, замечаем, что корень х2 = -2 не является его решением, так как при х = -2 правая часть уравнения 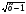 не определена. Дело в том, что возведение в квадрат привело нас к уравнению, которое не будет равносильно исходному. Таким образом, не сделав проверку, мы бы решили задачу неправильно.
не определена. Дело в том, что возведение в квадрат привело нас к уравнению, которое не будет равносильно исходному. Таким образом, не сделав проверку, мы бы решили задачу неправильно.
Ответ. х=2
Пример 2.Решить уравнение 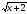 - х+1 =0,
- х+1 =0,
Решение. О.Д.З. х -2, х1=
-2, х1=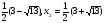 . Оба корня удовлетворяет О.Д.З., но только один корень удовлетворяет дополнительному ограничению х
. Оба корня удовлетворяет О.Д.З., но только один корень удовлетворяет дополнительному ограничению х 1, поэтому
1, поэтому
Ответ: 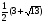
Ошибки:
* неправильно указано или не указано О.Д.З. Не учтено, что выражение под знаком корня четной степени должно быть неотрицательным;
* не учтено, что квадратный арифметический корень – неотрицательная величина, то он определен только для неотрицательных чисел;
* при возведении уравнения в квадрат не учтены знаки обеих его частей;
2.Дробно – рациональные уравнения:
Пример 1. Решить уравнение 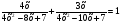 .
.
Решение. При х = 0 левая часть уравнения превращается в нуль, а правая часть отлична от нуля. Следовательно, х 0. Разделим числитель и знаменатель каждого из дробных членов левой части уравнения на х
0. Разделим числитель и знаменатель каждого из дробных членов левой части уравнения на х
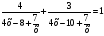
Предположим, 4х+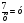 . Тогда данное уравнение преобразуется к виду
. Тогда данное уравнение преобразуется к виду
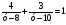 , откуда получим корни. Подставим эти значения в выражение для у, найдем корни заданного уравнения.
, откуда получим корни. Подставим эти значения в выражение для у, найдем корни заданного уравнения.
Ответ: х1 =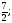 х2 =
х2 =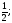
Пример 2. Решить уравнение: 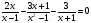 ;
;
Решение. О.Д.З. х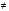 -1, х
-1, х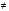 1. Приведем дроби к общему знаменателю и отбросим знаменатель 2х(х+1) – (3х+1) -3(х-1) = 0, 2х2 -4х + 2 = 0, х2+2х+1=0,
1. Приведем дроби к общему знаменателю и отбросим знаменатель 2х(х+1) – (3х+1) -3(х-1) = 0, 2х2 -4х + 2 = 0, х2+2х+1=0,
(х-1)2 = 0, х1 = х2 = 1, но х=1 О,Д,З
О,Д,З
Ответ: решений нет.
Ошибки:
*при получении ответа не учитывается О.Д.З.
* нерациональность в приведении к общему знаменателю;
Ошибка, общий знаменатель не должен обращаться нуль, х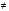 -1, х
-1, х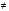 1 не входят в О.Д.З. поэтому ответ: решений нет.
1 не входят в О.Д.З. поэтому ответ: решений нет.
3.Алгебраические уравнения и неравенства.
Пример 1. Решить неравенство: –х2 - 5х - 6 0
0
Решение. Нужно отметить значения х, при которых график находится выше оси Ох. Приравнивая к нулю, находим нули функции. Следовательно, получаем ответ: -3 х
х -2
-2
Ошибки:
* неправильно изображен график квадратного трехчлена;
* неправильно определены значения аргумента, при которых неравенство выполняется;
* неверно использована теорема Виета и формула для нахождения корней;
Пример2. Решить неравенство: х2-2х 0
0

Решение. График функции у = х2 -2х – парабола, ветви направлены вверх. Находим нули функции, решая уравнение х2-2х = 0, х1 = 0, х2 = 2, график нашей функции проходит через эти точки.








х

0 ˚ ˚2
Ответ: (- ; 0)
; 0) (2;+
(2;+  )
)
Ошибки:
* деление на выражение, содержащее неизвестную величину;
* неправильно включены или не включены концы интервалов в
окончательный ответ.
Уравнения с модулем:
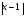 = 4, если х
= 4, если х 1, тогда уравнение
1, тогда уравнение
примет вид:
х -1 = 4, х = 5, если х 1, тогда уравнение примет вид
1, тогда уравнение примет вид
-х + 1 = 4, х = -3.
Ответ: -3; 5.
Ошибки:
*при снятии знака модуля не учтено, при каких условиях был
получен соответствующий корень;
* неправильно снят знак модуля, неверно использовано определение
модуля;
Текстовые задачи:
а) задачи на движение
Ошибки:
* неправильно введены неизвестные величины: введены неизвестные
величины, с помощью которых невозможно или трудно получить
ответ;
* неправильно поняты термины «позже», «раньше» и т.д.
* неправильно применены формулы средней скорости, пути;
* не учитывается, что скорость не может быть отрицательной;
* при выполнении преобразовании с величинами в разных единицах
Классификация по типам преобразования:
* неправильно раскрыли скобки;
* при переносе слагаемых из одной части в другую часть уравнения
или неравенства не сменили его знак на противоположный;
* неправильно привели подобные;
* неправильный порядок действий;
* неправильное применение формул сокращенного умножения;
* перепутаны степень и коэффициенты;
* разложение на множители или тождественные преобразования
иррациональных выражений;
* алгебраические ошибки при сложении и вычитании чисел с
одинаковыми и разными знаками, с дробями.
Грубые ошибки допускают при выполнении заданий базового уровня сложности по темам:
* преобразование логарифмических выражений;
* решение логарифмических неравенств с основаниями 0 а
а 1;
1;
* в формулах приведения получили неверный знак или функцию;
* неправильное преобразование сложной функции;
* использование неправильной области определения или свойств
функции sinx, cosx;
Учащиеся допускают ошибки в преобразовании разности логарифмов, частного, элементарных методов исследования свойств функций.
В перспективе на основе проделанной работы можно создать систему контроля и оценки уровня знаний учащихся.
Преподаватель математики: Сулейменова

 Получите свидетельство
Получите свидетельство Вход
Вход



 n, n
n, n x = ± arccos a + 2
x = ± arccos a + 2 Cos x =
Cos x = 

 n. n
n. n +
+ 2
2 2
2 Cos 3x = -
Cos 3x = -  +
+  n, n
n, n + 2
+ 2 , n
, n , x = (-1)n+1
, x = (-1)n+1
 2
2
 R
R ; у1,2 =
; у1,2 =  ; у1 =
; у1 = 
 возвращаемся к нашей замене sin x = y, sin x = 2,5 >1, нет решений
возвращаемся к нашей замене sin x = y, sin x = 2,5 >1, нет решений ; t1= 1,5; t = -1
; t1= 1,5; t = -1 . Уравнение
. Уравнение 2
2

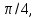
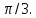
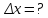
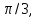 х=
х= 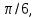 если
если  n, n
n, n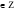
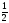 Cos x =
Cos x = 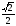

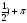 n. n
n. n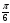 +
+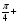 2
2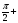 2
2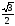 Cos 3x = -
Cos 3x = - 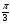 +
+ 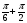
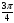 + 2
+ 2








 Решение тригонометрических уравнений введением новой переменной, применением формул. (140.63 KB)
Решение тригонометрических уравнений введением новой переменной, применением формул. (140.63 KB)
 0
0 1091
1091 10
10 Нравится
0
Нравится
0


