«Тождественные преобразования выражений»
Содержание.
| Введение | 3 |
| 3 |
|
4 |
| 4 |
| 5 |
| 5 |
| 9 |
| 9 |
| 10 |
|
12 |
| Заключение | 15 |
ВВЕДЕНИЕ.
Простейшие преобразования выражений и формул, опирающиеся на свойства арифметических операций, производятся в начальной школе и 5 и 6 классах. Формирование умений и навыков выполнения преобразований происходит в курсе алгебры. Это связано как с резким увеличением числа и разнообразия совершаемых преобразований, так и с усложнением деятельности по их обоснованию и выяснению условий применимости, с выделением и изучением обобщенных понятий тождества, тождественного преобразования, равносильного преобразования.
Понятие тождества.
Тождество – это равенство, верное при любых значениях переменных.
Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.
Тождественное равенство обозначают символом «≡» (тройное равенство).
Тождественное преобразование выражения – это замена исходного выражения на выражение, тождественно равное ему.
Часто в этом словосочетании слово «тождественное» опускается, и говорят просто «преобразование выражения», при этом подразумевают, что речь идет именно о тождественном преобразовании.
Для тождественных преобразований используют формулы сокращенного умножения, законы арифметики и другие тождества.
При выполнении тождественных преобразований алгебраических выражений необходимо знать порядок выполнения действий, действия с дробями и степенными выражениями, формулы сокращенного умножения и др.
Следует иметь в виду, что при тождественных преобразованиях остаются неизменными:
- величина допустимых изменений буквенных величин;
- область допустимых значений каждой из буквенных величин.
Однако это не значит, что мы должны отказываться от таких преобразований, которые изменяют области допустимых значений величин. Напротив, мы ими часто пользуемся и при упрощении выражений и при решении уравнений. Нужно только при каждом таком преобразовании указать, как изменились области допустимых значений буквенных величин.
Порядок выполнения действий при тождественных преобразованиях.
Порядок выполнения действий:
- действия с одночленами;
- действия в скобках;
- умножение или деление (в порядке появления);
- сложение или вычитание (в порядке появления).
Основные тождественные преобразования.
Существует ряд наиболее часто используемых тождественных преобразований, которые проводятся с выражениями различных видов.
Такие преобразования назовем основными:
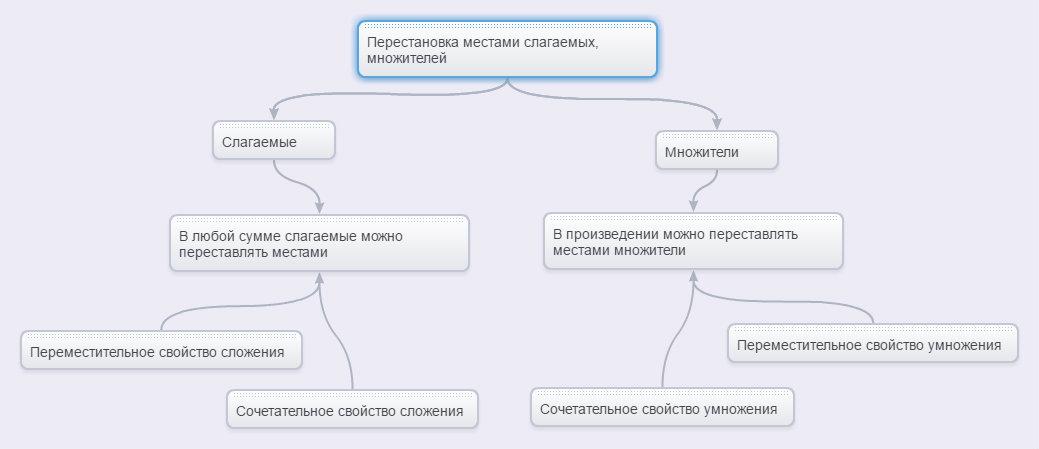
Перестановка местами слагаемых, множителей
Справедливо правило: в любой сумме слагаемые или в любом произведении множители можно переставлять местами.
Это правило вытекает из переместительного и сочетательного свойств сложения и произведения. Из этих свойств следует, что все выражения, полученные после перестановки местами слагаемых (или множителей), тождественно равны исходному выражению. Поэтому, перестановка местами слагаемых в сумме (или множителей в произведении) является тождественным преобразованием.
Раскрытие скобок.
Числовые выражения и выражения с переменными в своей записи могут содержать скобки. Эти выражения можно заменить тождественно равными выражениями, в которых будет меньшее количество скобок или их не будет вовсе.
Правило раскрытия скобок, в которые заключены одиночные положительные числа: пусть a – положительное число, тогда (a) заменяется на a, +(a) заменяется на +a и −(a) заменяется на −a.
Правило раскрытия скобок, в которых содержатся одиночные отрицательные числа: +(−a) заменяется на −a, а −(−a) заменяется на +a, если же выражение начинается с отрицательного числа (−a), записанного в скобках, то скобки, содержащие это число, просто опускаются, и вместо (−a) остается −a.
Правило раскрытия скобок в произведении двух чисел.
Пусть a и b – положительные числа. Тогда произведение двух отрицательных чисел −a и −b вида (−a)·(−b) заменяется на (a·b), а произведения двух чисел с противоположными знаками вида (−a)·b и a·(−b) заменяются на (−a·b).
Иными словами, умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.
Аналогичное правило справедливо и для частного двух чисел, так как деление можно рассматривать как умножение на обратное число.
| Раскрытие скобок | ||||
| При сложении | При умножении | |||
| Положительных чисел | Отрицательных чисел | Чисел с одинаковыми знаками | Чисел с разными знаками | |
| (а) + … = а + … | (-а) + …= -а + … | (а)∙(b) = (a∙b) = = a∙b | (- а)∙(b) = (- a∙b) = = - a∙b | |
| … + (а) = … + а | … + (-а) = … - а | (-a)∙(-b) = (a∙b) = = a∙b | (а)∙(- b) = (- a∙b) = = - a∙b | |
|
| … - (-а) = … + а |
|
| |
Для раскрытия скобок, содержащих произведение нескольких отрицательных чисел, следует руководствоваться следующим правилом:
Если количество отрицательных чисел четно, то можно опустить скобки, заменив эти числа противоположными, после чего заключить полученное выражение в новые скобки; если же количество отрицательных чисел нечетно, то нужно опустить скобки, заменить эти числа на противоположные, поставить минус перед полученным выражением и заключить его в скобки.
Раскрытие скобок при умножении числа на скобку, выражения на скобку.
Раскрытие скобок в этих случаях проводится с использованием формул вида
 ,
,
где  и
и  – некоторые числа или выражения.
– некоторые числа или выражения.
Умножение скобки на скобку
Чтобы умножить одну сумму на другую, надо каждое слагаемое первой суммы умножить на каждое слагаемое второй суммы и сложить полученные произведения:

=
+
+
Деление скобки на число и скобки на скобку.
При делении скобки на число можно раскрыть скобки, разделив на это число каждое из заключенных в скобки слагаемых.
Не менее удобно предварительно деление заменить умножением, после чего воспользоваться соответствующим правилом раскрытия скобок в произведении. Это правило позволяет раскрывать скобки и при делении скобки на скобку.
Порядок раскрытия скобок.
Порядок раскрытия скобок в алгебраических выражениях согласован с порядком выполнения действий:
сначала выполняется возведение скобок в натуральную степень,
дальше раскрываются скобки в произведениях и частных,
наконец, когда скобок в произведениях не остается, раскрываются скобки в суммах и разностях.
Задание для интерактивной доски: необходимо соотнести выражения и тождественно равными им.

Группировка слагаемых, множителей
К суммам трех и большего количества слагаемых применимо тождественное преобразование, получившее название группировка слагаемых. Под группировкой слагаемых понимают объединение нескольких слагаемых в группу, путем их перестановки и заключения в скобки. То есть, при группировке слагаемые переставляются местами так, чтобы группируемые слагаемые оказались рядом, после чего они заключаются в скобки.
Аналогично в произведениях трех, четырех и т.д. множителей может быть проведена группировка множителей.
Вынесение за скобки общего множителя
Когда слагаемые в выражении имеют одинаковый множитель, то с таким выражением можно провести преобразование, которое называется вынесением за скобки общего множителя. При этом преобразовании исходное выражение представляется в виде произведения общего множителя и выражения в скобках, состоящего из исходных слагаемых без общего множителя.
В основе вынесения общего множителя за скобки лежит распределительное свойство умножения относительно сложения, которое задается равенством a·(b+c)=a·b+a·c. Поменяв в этом равенстве местами левую и правую часть, оно примет вид a·b+a·c=a·(b+c), откуда становится видно, что правая его часть равна левой части, в которой вынесен за скобки общий множитель a.
Задание для интерактивной доски:

Приведение подобных слагаемых
Данное тождественное преобразование относится к суммам, содержащим подобные слагаемые, то есть одинаковые слагаемые или слагаемые, отличающиеся только числовым коэффициентом. Оно получило название приведение подобных слагаемых.
Суть приведения подобных слагаемых заключается в вынесении общей буквенной части подобных слагаемых за скобки, и в последующем вычислении суммы числовых коэффициентов в скобках.
Задание для интерактивной доски:
Соотнести тождественные выражения:
Памятка «Тождественные преобразования алгебраических выражений».
Действия с дробями:
| Сложение | Вычитание | Умножение | Деление |
|
|
|
|
|
Перестановка членов пропорции:
|
|
|
|
|
Производные пропорции.
Дана пропорция  , справедливы следующие пропорции:
, справедливы следующие пропорции:
|
|
|
Формулы сокращенного умножения:
|
| |
| | |
|
где
| |
Формулы корней квадратного уравнения
|
| ||
| | | |
| | | Среди действительных чисел корней нет |
Формулы корней приведенного квадратного уравнения
|
| ||
| | | |
| | | Среди действительных чисел корней нет |
Теорема Виета. В приведенном квадратном уравнении
сумма корней равна коэффициенту при
, взятому с противоположным знаком, а их произведение – свободному члену:
Если задано квадратное уравнение в общем виде: , то делением уравнения на
можно свести к приведенному,
где ,
Действия со степенями:
| | | |
| | | |
При работе с модулями используют различные свойства модулей, например:
| | | | | |
Действия с корнями (корни предполагаются арифметическими):
| | | |
| | | |
| | | |
Свойства числовых неравенств
пусть ,
, тогда
пусть ,
, тогда
Заключение.
Тождественные преобразования представляют из себя одну из главных линий школьного курса математики. На их основании у обучащихся формируется представления об аналитических методах математики. Как правило, при выполнении практически любого задания по алгебре выполняется тождественные преобразования.
Необходимо иметь ввиду: в школьном курсе математики очень часто делают неравносильные преобразования, и при этом происходит расширения или сужение области определения. Обучащиеся должны понимать, что в данном случае нужно сделать проверку при решении или уравнения или найти область определения при решении неравенства.
4

 Получите свидетельство
Получите свидетельство Вход
Вход












 Реферат на тему "Тождественные преобразования выражений" (599.23 KB)
Реферат на тему "Тождественные преобразования выражений" (599.23 KB)
 0
0 3313
3313 65
65 Нравится
0
Нравится
0






