Проектирование системы равносильных преобразований в классе иррациональных уравнений

2.4. Проектирование системы равносильных преобразований в классе иррациональных уравнений.

В классе иррациональных уравнений деятельность по использованию равносильных преобразований состоит из следующих базовых действий:

1. Выделить систему равносильных преобразований иррациональных уравнений стандартного вида.

2. Выделить систему равносильных преобразований, приводящих к иррациональным уравнениям стандартного вида.

Деятельность по формированию равносильных преобразований иррациональных уравнений стандартного вида состоит из следующих базовых действий:

1. Уравнение 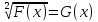равносильно системе 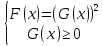, то есть уравнению 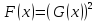на множестве M={x|}.

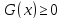2. Уравнение 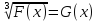равносильно системе .

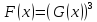Деятельность по формированию равносильных преобразований приводящих к иррациональным уравнениям стандартного вида состоит из следующих базовых действий:

1. Уравнение 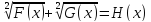(1) равносильно уравнению 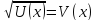(2) на множестве M={x|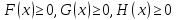}, где U(x)=F(x)∙G(x), .

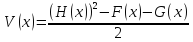2. Уравнение 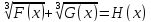(3) равносильно уравнению 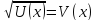(4) на множестве M={x|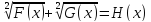}, где U(x)=F(x)∙G(x), .

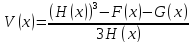Действия по формированию выделенных свойств равносильности опираются на три различных понятия равносильности:

Опр. 1 Уравнения 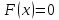и 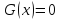называются равносильными на М, если множества их решений на множестве М совпадают.

Опр. 2 Уравнение 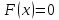равносильно совокупности уравнени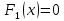й и 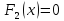, если множество решений 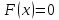совпадает с объединением множеств решени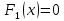й и .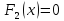

Опр. 3 Уравнения 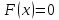и 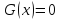называются равносильными если:

1. Область определения уравнений совпадает

2. Множество их решений совпадают

Представим поэтапное формирование действия равносильного преобразования уравнения, содержащего сумму иррациональных уравнений с чётной степенью радикала к иррациональному уравнению стандартного вида I.

Данное действие в школьном курсе представлено в виде теоремы:

Уравнение 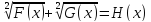(1) равносильно уравнению 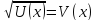(2) на множестве M={x|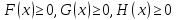}, где U(x)=F(x)∙G(x), .

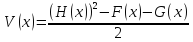Формирование данного равносильного преобразования заключается в обосновании равносильного перехода от одного иррационального уравнения к другому на области определения М многочленов.

Представим процесс поэтапного формирования данного действия на трех последовательных уровнях сформированности на множестве М.

Методическая задача формирования деятельности в классе иррациональных уравнений вида 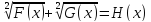(1) на материализованном уровне имеет следующую формулировку:

Сформировать понятие равносильного перехода от уравнения (1) к уравнению (2).

Реализация данной методической задачи на материализованном уровне с учётом его критериальных признаков осуществляется в дидактической задаче:

Установить равносильность уравнения (5) и (6) на множестве М={x|} в содержании полного операционного состава, то есть для уравнений (5) и (6)

установить:

1. способ перехода от уравнения (5) к уравнению (6) и его цель;

2. будут ли решения уравнения (6) решениями уравнения (5);

3. что в уравнении (5) других решений нет;

4. равносильность или не равносильность уравнений (5) и (6).

а) Для решения уравнения (5) необходимо осуществить переход на множестве М={x|} к уравнению (6) стандартного вида, имеющему общий способ решения. Данный переход позволяет множество решений уравнения (6) рассматривать в качестве множества решений уравнения (5). Переход осуществляется с помощью возведения в квадрат обеих частей уравнения (5).

б) на основании метода решения иррациональных уравнений стандартного вида установлено, что х=1- решение иррационального уравнения (6). Проверим, является ли данное значение решением уравнения (5) на множестве М={x|}. Подстановка значения показывает, что решение уравнения (6) является решением уравнения (5).

в) Предположим, что x=a – решение уравнения (5). Тогда при подстановке числа a в уравнение (5), оно обращается в верное числовое равенство . Возведём обе части уравнения в квадрат и перенесём в правую часть слагаемые не имеющие знака корня. Получим уравнение равносильное данному на множестве М={a|}: , откуда а=1. Таким образом, уравнение (5) на множестве М={x|} других решений не имеет.

г) Поскольку множество решений уравнения (5) и множество решений уравнения (6) совпадают на множестве М={x|}, то можно утверждать, что уравнения (5) и (6) равносильны на множестве М.

Согласно зафиксированному материализованному уровню сформулируем определение равносильности уравнений:

Уравнение равносильно уравнению , если на их общей области определения множества решений совпадают.

Операционный состав действия по проверке равносильности двух уравнений позволяет выделить «уровень имён». Дидактическая задача адекватная «уровню имён» действия реализуется в следующем операционном составе:

1. Связь уравнений и цель перехода.

2. Общие решения уравнений (5) и (6).

3. Отсутствие других решений уравнений (5) и (6).

4. Равносильность уравнений.

Сформированные материализованный уровень и «уровень имён» позволяют перейти к формированию внешнеречевого уровня действия равносильного преобразования уравнения, содержащего сумму иррациональных уравнений чётной степени к иррациональному уравнению стандартного вида I. Методическая задача данного уровня формулируется следующим образом:

На основе выделенного закономерного «уровня имен» установить способ равносильного перехода от иррационального уравнения, содержащего сумму иррациональных уравнений чётной степени, к иррациональному уравнению стандартного вида I и обосновать его общность на примере конкретного иррационального уравнения данного класса.

Исходя из методической задачи, формирование данной деятельности на внешнеречевом уровне характеризуется становлением общего способа деятельности вместе с процессом его конкретизации в системе следующих дидактических задач:

1. Установить общий способ обоснования равносильности уравнени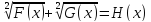й (1) и 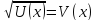(2) на множестве M={x|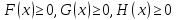}, где U(x)=F(x)∙G(x), , в системе последовательных действий.

2. Провести конкретизацию каждого действия в содержании следующей задачи: Установить равносильность уравнения (7) и (8) на множестве М={x|} в соответствии с общим способом обоснования равносильности.

1. О. Для решения уравнения 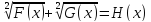(1) необходимо осуществить переход на множестве M={x|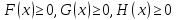} к уравнению 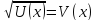(2) стандартного вида, имеющему общий способ решения. Для осуществления равносильного перехода от уравнения (1) к уравнению (2) на множестве M необходимо выполнить следующие равносильные преобразования:

1. возвести обе части уравнения в квадрат;

2. перенести в правую часть уравнения все выражения, не имеющие знака корня;

3. разделить обе части уравнения на 2.

Данный переход позволит множество решений уравнения (2) рассматривать в качестве множества решений уравнения (1).

К. Для решения уравнения (7) необходимо осуществить переход на множестве М={x|} к уравнению Это позволит множество решений уравнения (8) рассматривать в качестве множества решений уравнения (7). Данный переход осуществляется возведением обеих частей уравнения в квадрат.

2. О. Покажем, что множество решений уравнения (1) включается во множество решений уравнения (2). Пусть x=a включается в множество решений уравнения (2). Тогда , где U(a)=F(a)∙G(a), на множестве M={a|} – верное числовое равенство.

Подставим в уравнение (*) значения выражений U(a) и (**).

Умножив обе части уравнения (**) на (-2) получим уравнение равносильное данному: .

Перенесём в левую часть уравнения выражения F(а) и G(а) с противоположным знаком и получим уравнение равносильное данному:

- .

Так как F(a)≥0 и G(a)≥0,то по свойству арифметического квадратного корня , . Тогда уравнение примет вид:

.

Заменим левую часть уравнения тождественно равным выражением:

.

Данное уравнение на множестве равносильного преобразования равносильно уравнению: (1). Значит уравнение (1) тоже является верным числовым равенством. Следовательно, х=а – решение уравнения (1) на множестве M={x|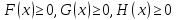}. Таким образом, множество решений уравнения (2) включается в множество решений уравнения (1).

К. Найдём все решения уравнения (8): х=1 и х=. Так как всякое решение уравнения (2) является решением уравнения (1), то х=1 и х= – решения уравнения (7).

3. О. Покажем, что уравнение (1) других решений, кроме найденных, не имеет. Предположим, что х=b включается во множество решений уравнения (1). Тогда для числа b уравнение – верное числовое равенство. Но уравнение равносильно уравнению . Значит, - верное числовое равенство. Следовательно х=b – решение уравнения (2). Таким образом, уравнение (1) других решений, кроме решений уравнения (2), не имеет.

К. Покажем, что уравнение (7) других решений, кроме найденных, не имеет. Предположим, что х=b включается во множество решений уравнения (7). Тогда для числа b уравнение – верное числовое равенство. Но уравнение равносильно уравнению . Значит, - верное числовое равенство. Следовательно х=b – решение уравнения (8). Но решениями уравнения (8) являются х=1 и х= . Следовательно, либо b=1 либо b=. Таким образом, уравнение (7) других решений, кроме решений уравнения (8), не имеет.

4. О. Если множество решений уравнения (1) совпадает с множеством решений уравнения (2) на множестве M={x|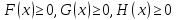}, то уравнения (1) и (2) равносильны. В противном случае уравнения неравносильны.

К. Поскольку множество решений уравнения (7) совпадает с множеством решений уравнения (8) на множестве М={x|}, то уравнения (7) и (8) равносильны.

Внешнеречевая (обобщенная) форма определения имеет вид:

Уравнение 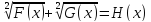равносильно уравнению 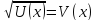, где U(x)=F(x)∙G(x), 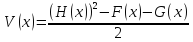, если на их общей области определения множества решений совпадают.

Внутренний уровень действия «равносильные преобразования уравнения, содержащего сумму иррациональных уравнений чётной степени, к иррациональному уравнению стандартного вида I» реализуется в методической задаче: осуществить перенос общего способа обоснования равносильности уравнения, содержащего сумму иррациональных уравнений чётной степени, и иррационального уравнения стандартного вида I на класс иррациональных уравнений с параметром и переменной.

Решение методической задачи осуществляется в следующей дидактической задаче:

1. На базе общего способа обоснования равносильности уравнений (1) и (2) на множестве M={x|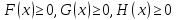} установить действия обобщённого способа обоснования равносильности уравнений (1’) и (2’) на множестве M={(a,x)|, где U(a,x)=F(a,x)∙G(a,x), .

2. Выделенное действие реализовать в обосновании равносильности уравнений с параметром и переменной:

(*) и на множестве M={(a,x)|.

1. Установить общий способ обоснования равносильности уравнений (1’) и (2’) с параметром и переменной.

В процессе решения дидактической задачи осуществляется достижение следующих частных методических задач:

1. по каждому из действий обобщенного способа обоснования равносильности иррационального уравнения, содержащего сумму иррациональных уравнений чётной степени, и иррационального уравнения стандартного вида I сформулировать гипотетическое аналоговое действие (деятельность) в классе иррациональных уравнений с параметром и переменной в форме конкретной цели (Ц);

2. на конкретных уравнениях с параметром и переменной осуществить действие для установления правильности выдвинутой гипотезы (К);

3. зафиксировать обобщенную форму действия для всех иррациональных уравнений с параметром и переменной вида (1’) (О).

1) Ц. Укажем цель и способ перехода от уравнения, содержащего в левой части сумму иррациональных выражений чётной степени, к иррациональному уравнению стандартного вида I.

К. Для решения уравнения (*) необходимо осуществить переход на множестве M={(a,x)| к уравнению

Это позволит множество решений уравнения (**) рассматривать в качестве множества решений уравнения (*).

О. Для решения уравнения (1’) необходимо осуществить переход на множестве M={(a,x)| к уравнению (2’), где U(a,x)=F(a,x)∙G(a,x), стандартного вида, имеющему общий способ решения. Для осуществления равносильного перехода уравнения (1’) к уравнению (1’) на множестве M необходимо выполнить следующие равносильные преобразования:

1. возвести обе части уравнения в квадрат;

2. перенести в правую часть уравнения все выражения не имеющие знака корня;

3. разделить обе части уравнения на 2.

2) Ц. Обосновать равносильность перехода, доказав включённость множества решений уравнения стандартного вида в множество решений уравнения, содержащего в левой части сумму иррациональных выражений, на множестве определения уравнений.

О. Покажем, что множество решений уравнения (1’) включается во множество решений уравнения (2’). Пусть x=c включается в множество общих решений уравнения (2’). Тогда , где U(a,c)=F(a,c)∙G(a,c), – верное числовое равенство.

Подставим в уравнение значения выражений U(a,c) и .

Умножив обе части этого уравнения на два, получим уравнение равносильное данному: .

Перенесём в левую часть уравнения выражения F(а,c) и G(а,c) с противоположным знаком и получим уравнение равносильное данному:

.

Так как F(a,c)≥0 и G(a,c)≥0,то по свойству арифметического квадратного корня , . Тогда уравнение примет вид:

.

Заменим левую часть уравнения тождественно равным выражением и получим равносильное уравнение:

.

Данное уравнение на множестве равносильного преобразования равносильно уравнению: (1). Значит уравнение (1’) тоже является верным числовым равенством. Следовательно, х=c – решение уравнения (1’) на множестве M={x|}. Таким образом, множество решений уравнения (2’) включается в множество решений уравнения (1’).

К. Найдём все общие решения уравнения : . Так как всякое решение уравнения (2’) является решением уравнения (1’), то – общее решения уравнения на множестве M={(a,x)|.

3. Ц. Обосновать равносильность перехода, доказав включённость множества решений уравнения, содержащего в левой части сумму иррациональных выражений, в множество решений уравнения стандартного вида на множестве определения уравнений.

О. Покажем, что уравнение (1’) других решений, кроме найденных, не имеет. Предположим, что х=d включается во множество решений уравнения (1’). Тогда для числа d уравнение – верное числовое равенство. Но уравнение равносильно уравнению . Значит, - верное числовое равенство. Следовательно х=b – решение уравнения (2’). Таким образом, уравнение (1’) других решений, кроме решений уравнения (2’), не имеет.

К. Покажем, что уравнение (*) других решений, кроме найденных, не имеет. Предположим, что х=n включается во множество решений уравнения (*). Тогда для числа n уравнение – верное числовое равенство. Но уравнение равносильно уравнению . Значит, - верное числовое равенство. Следовательно х=n – решение уравнения (**). Но общее решение уравнения (**) имеет вид . Следовательно, уравнение (*) других решений, кроме решений уравнения (**), не имеет.

4) Ц. Сделать вывод о равносильности уравнений на основе определения равносильности и на основе предыдущих пунктов.

К. Поскольку множество решений уравнения совпадает с множеством решений уравнения (**) на множестве M={(a,x)|, то уравнения (*) и (**) равносильны.

О. Если множество решений уравнения (1’) совпадает с множеством решений уравнения (2’) на множестве M={(a,x)|, где U(a,x)=F(a,x)∙G(a,x), , то по определению равносильности уравнений уравнения (3’) и (4’) равносильны. В противном случае уравнения неравносильны.

Внутренняя форма определения равносильности иррациональных уравнений с параметром имеет вид:

Уравнение для любого допустимого значения параметра а равносильно уравнению(2’), где U(a,x)=F(a,x)∙G(a,x), , если на их общей области определения множества решений совпадают.

Вторым действием в системе равносильных преобразований является действие по равносильному преобразованию на множестве М иррациональных уравнений с нечётной степенью радикала.

Указанное равносильное преобразование в математике школьного курса представлено теоремой:

Уравнение 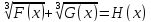(3) равносильно на множестве M={x|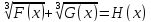} уравнению (4), где U(x)=F(x)∙G(x), .

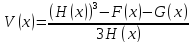Формирование данного равносильного преобразования заключается в обосновании равносильности перехода от иррационального уравнения, содержащего в левой части сумму иррациональных выражений нечётной степени радикала, к иррациональному уравнению стандартного вида I, на области определения М уравнений.

Целью действия выступает обоснование равносильности уравнения (3) и уравнения (4).

Представим процесс поэтапного формирования действия по равносильному преобразованию на множестве М одного иррационального уравнения к другому иррациональному уравнению на трех последовательных уровнях сформированности.

Методическая задача формирования деятельности в классе иррациональных уравнений вида 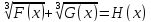(3) на материализованном уровне имеет следующую формулировку:

Сформировать понятие равносильного перехода от уравнения (3) к уравнению (4).

Реализация данной методической задачи на материализованном уровне с учётом его критериальных признаков осуществляется в дидактической задаче:

Установить равносильность уравнения (7) и (8) на множестве М={x|} в содержании полного операционного состава, то есть для уравнений (7) и (8)

установить:

1. способ перехода от уравнения (7) к уравнению (8) и его цель;

2. будут ли решения уравнения (8) решениями уравнения (7);

3. что в уравнении (7) других решений нет;

4. равносильность или не равносильность уравнений (7) и (8).

а) Для решения уравнения (7) необходимо осуществить переход на множестве М={x|} к уравнению стандартного вида, имеющему общий способ решения. Данный переход позволяет множество решений уравнения (8) рассматривать в качестве множества решений уравнения (7). Переход осуществляется с помощью возведения в третью степень обеих частей уравнения (7).

б) на основании метода решения иррациональных уравнений стандартного вида установлено, что х=-3, х=-1/2, х=2 - решения иррационального уравнения (8). Проверим, является ли данные значения решениями уравнения (7) на множестве М={x|}. Подстановка значения показывает, что решения уравнения (8) являются решениями уравнения (7).

в) Предположим, что x=a – решение уравнения (7). Тогда при подстановке числа a в уравнение (7), оно обращается в верное числовое равенство . Возведём обе части уравнения в третью степень и перенесём в правую часть слагаемые не имеющие знака корня. Получим уравнение равносильное данному на множестве М={a|}: , откуда a=-3, a=-1/2, a=2. Таким образом, уравнение (7) на множестве М={x|} других решений не имеет.

г) Поскольку множество решений уравнения (7) и множество решений уравнения (8) совпадают на множестве М={x|}, то можно утверждать, что уравнения (7) и (8) равносильны на множестве М.

Согласно зафиксированному материализованному уровню сформулируем определение равносильности уравнений:

Опр.1 Уравнение равносильно уравнению , если на их общей области определения множества решений совпадают.

Операционный состав действия по проверке равносильности двух уравнений позволяет выделить «уровень имён». Дидактическая задача адекватная «уровню имён» действия реализуется в следующем операционном составе:

1. Связь уравнений и цель перехода.

2. Общие решения уравнений (7) и (8).

3. Отсутствие других решений уравнений (7) и (8).

4. Равносильность уравнений.

Сформированные материализованный уровень и «уровень имён» позволяют перейти к формированию внешнеречевого уровня действия равносильного преобразования уравнения, содержащего сумму иррациональных уравнений нечётной степени к иррациональному уравнению стандартного вида I. Методическая задача данного уровня формулируется следующим образом:

На основе выделенного закономерного «уровня имен» установить способ равносильного перехода от иррационального уравнения, содержащего сумму иррациональных уравнений нечётной степени, к иррациональному уравнению стандартного вида I и обосновать его общность на примере конкретного иррационального уравнения данного класса.

Исходя из методической задачи, формирование данной деятельности на внешнеречевом уровне характеризуется становлением общего способа деятельности вместе с процессом его конкретизации в системе следующих дидактических задач:

1. Установить общий способ обоснования равносильности уравнений 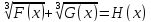(3) и (4) на множестве М={x|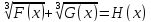}, где U(x)=F(x)∙G(x), 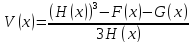в системе последовательных действий.

2. Провести конкретизацию каждого действия в содержании следующей задачи: Установить равносильность уравнения и (10) на множестве М={x|} в соответствии с общим способом обоснования равносильности.

1. О. Для решения уравнения 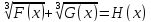(3) необходимо осуществить переход на множестве М={x|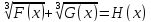} к уравнению (4) стандартного вида, имеющему общий способ решения. Для осуществления равносильного перехода уравнения (3) к уравнению (4) на множестве M необходимо выполнить следующие равносильные преобразования:

1. возвести обе части уравнения в третью степень;

2. перенести в правую часть уравнения все выражения не имеющие знака корня;

3. разделить обе части уравнения на 3H(x).

Данный переход позволит множество решений уравнения (4) рассматривать в качестве множества решений уравнения (3).

К. Для решения уравнения необходимо осуществить переход на множестве М={x|} к уравнению Это позволит множество решений уравнения (10) рассматривать в качестве множества решений уравнения (9). Данный переход осуществляется возведением обеих частей уравнения в квадрат.

2. О.

К. Найдём все решения уравнения (10): х= -1 и х= Так как всякое решение уравнения (4) является решением уравнения (3), то х=-1 и х= – решения уравнения .

3. О.

К. Покажем, что уравнение (9) других решений, кроме найденных, не имеет. Предположим, что х=b включается во множество решений уравнения (9). Тогда для числа b уравнение – верное числовое равенство. Но уравнение равносильно уравнению . Значит, - верное числовое равенство. Следовательно х=b – решение уравнения . Но решениями уравнения (10) являются х= -1 и х= . Следовательно, либо b=-1 либо b=. Таким образом, уравнение (9) других решений, кроме решений уравнения (10), не имеет.

4. О. Если множество решений уравнения (3) совпадает с множеством решений уравнения (4) на множестве М={x|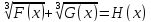}, то уравнения (3) и (3) равносильны. В противном случае уравнения неравносильны.

К. Поскольку множество решений уравнения совпадает с множеством решений уравнения (10) на множестве М={x|}, то уравнения (9) и (10) равносильны.

Внешнеречевая (обобщенная) форма определения имеет вид:

Уравнение 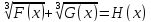(3) равносильно уравнению (4), где U(x)=F(x)∙G(x), , если на их общей области определения множества решений совпадают.

Внутренний уровень действия «равносильные преобразования уравнения, содержащего сумму иррациональных уравнений нечётной степени, к иррациональному уравнению стандартного вида I» реализуется в методической задаче: осуществить перенос общего способа обоснования равносильности уравнения, содержащего сумму иррациональных уравнений нечётной степени, и иррационального уравнения стандартного вида I на класс иррациональных уравнений с параметром и переменной.

Решение методической задачи осуществляется в следующей дидактической задаче:

1. На базе общего способа обоснования равносильности уравнений (3) и (4) на множестве М={x|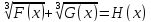} установить действия обобщённого способа обоснования равносильности уравнений (3’) и (4’) на множестве M={(a,x)|}, где U(a,x)=F(a,x)∙G(a,x), .

2. Выделенное действие реализовать в обосновании равносильности уравнений (11) и (12) с параметром и переменной:

(11)

(12)

1. Установить общий способ обоснования равносильности уравнений (3’) и (4’) с параметром и переменной.

В процессе решения дидактической задачи осуществляется достижение следующих частных методических задач:

1. по каждому из действий обобщенного способа обоснования равносильности иррационального уравнения, содержащего сумму иррациональных уравнений нечётной степени, и иррационального уравнения стандартного вида I сформулировать гипотетическое аналоговое действие (деятельность) в классе иррациональных уравнений с параметром и переменной в форме конкретной цели (Ц);

2. на конкретных уравнениях с параметром и переменной осуществить действие для установления правильности выдвинутой гипотезы (К);

3. зафиксировать обобщенную форму действия для всех иррациональных уравнений с параметром и переменной вида (3’) (О).

1) Ц. Укажем цель и способ перехода от уравнения, содержащего в левой части сумму иррациональных выражений, к иррациональному уравнению стандартного вида I.

К. Для решения уравнения (11) необходимо осуществить переход на множестве M={(a,x)| к уравнению (12).

Это позволит множество решений уравнения (12) рассматривать в качестве множества решений уравнения (11).

О. Для решения уравнения (3’) необходимо осуществить переход на множестве М={x|} к уравнению (4’) стандартного вида, имеющему общий способ решения. Для осуществления равносильного перехода уравнения (3’) к уравнению (4’) на множестве M необходимо выполнить следующие равносильные преобразования:

1. возвести обе части уравнения в третью степень;

2. перенести в правую часть уравнения все выражения не имеющие знака корня;

3. разделить обе части уравнения на 3H(x).

2) Ц. Обосновать равносильность перехода, доказав включённость множества решений уравнения стандартного вида в множество решений уравнения, содержащего в левой части сумму иррациональных выражений, на множестве определения уравнений.

К.

О.

3) Ц. Обосновать равносильность перехода, доказав включённость множества решений уравнения, содержащего в левой части сумму иррациональных выражений, в множество решений уравнения стандартного вида на множестве определения уравнений.

К.

О.

4) Ц. Сделать вывод о равносильности уравнений на основе определения равносильности и на основе предыдущих пунктов.

К. Поскольку множество решений уравнения (11) совпадает с множеством решений уравнения (12) на множестве M={(a,x)|, то уравнения (11) и (12) равносильны.

О. Если множество решений уравнения (3’) совпадает с множеством решений уравнения (4’) на множестве M={(a,x)|, где U(a,x)=F(a,x)∙G(a,x), , то по определению равносильности уравнений уравнения (3’) и (4’) равносильны. В противном случае уравнения неравносильны.

Внутренняя форма определения равносильности иррациональных уравнений с параметром имеет вид:

Уравнение для любого допустимого значения параметра а равносильно уравнению(4’), где U(a,x)=F(a,x)∙G(a,x), если на их общей области определения множества решений совпадают.

4