Презентация на тему : "Дискретное преобразование Фурье"

Дискретное преобразование Фурье

• Объект исследования преобразование Фурье.
• Предмет исследования дискретное преобразование Фурье.
• Целью исследования является исследование, систематизация, обобщение знаний о ДПФ и его применение в различных областях науки и техники.
• Перед началом работы были поставлены следующие задачи:
• рассмотреть и проанализировать библиографические источники по данной теме;
• рассмотреть такие понятия как: преобразования Фурье, дискретное преобразование Фурье (прямое и обратное), быстрое преобразование Фурье;
• выявить целесообразность использования дискретного преобразования Фурье, указать области его применения;
• разработать алгоритм дискретного и быстрого преобразования Фурье.

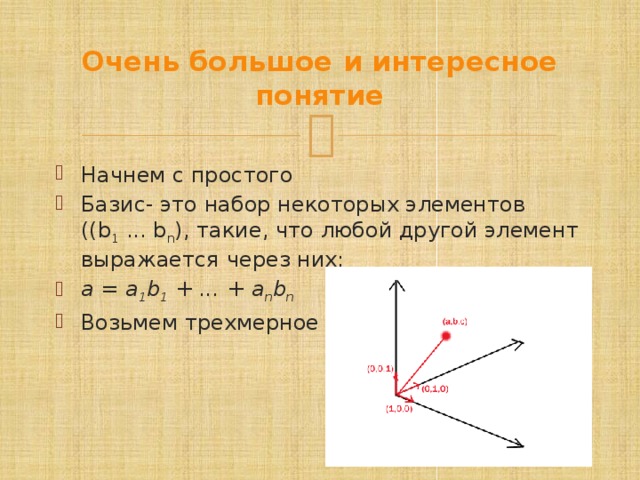
Очень большое и интересное понятие

• Начнем с простого
• Базис- это набор некоторых элементов ((b 1 ... b n ), такие, что любой другой элемент выражается через них:
• a = a 1 b 1 + ... + a n b n
• Возьмем трехмерное пространство

Элементы (1,0,0), (0,1,0) и (0,0,1) являются базисом

• (a, b, c) = a(1, 0, 0) + b(0, 1, 0) + c(0, 0, 1)
• (1,0,1), (0,1,1), (1,1,0).
• как можно произвольный элемент разложить в базис
• (a, b, c)(x, y, z) = ax + by + cz;

v 1 , v 2 и v 3 выполняется следующее: v 1 ( v 2 + v 3 ) = v 1 v 2 + v 1 v 3

• Если v 1 v 2 = 0, то эти элементы ортогональны
• b 1 b 2 = 0 b 1 b 3 = 0 b 2 b 3 = 0
• допустим наш элемент раскладывается в базис вот так: v = x b 1 + y b 2 + z b 3
• Как узнать x, y и z?
• vb 1 = (x b 1 + y b 2 + z b 3 ) b 1 = x b 1 b 1
• vb 2 = (x b 1 + y b 2 + z b 3 ) b 2 = y b 2 b 2
• vb 3 = (x b 1 + y b 2 + z b 3 ) b 3 = z b 3 b 3

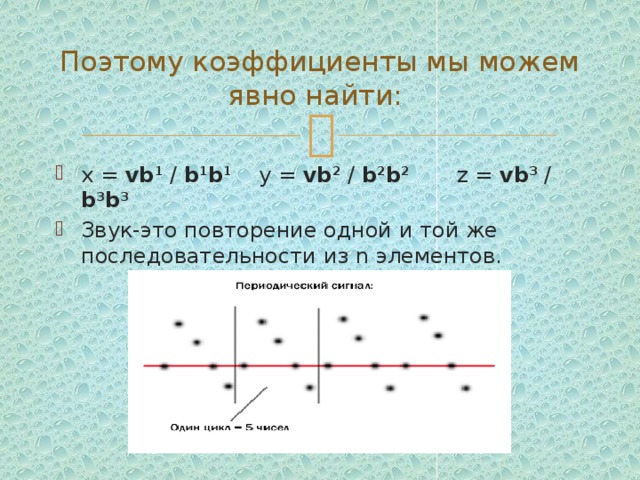
Поэтому коэффициенты мы можем явно найти:

• x = vb 1 / b 1 b 1 y = vb 2 / b 2 b 2 z = vb 3 / b 3 b 3
• Звук-это повторение одной и той же последовательности из n элементов.

(f 1 ... f n ) Прямое преобразование Фурье. (f 1 ... f n ) - (a 1 ... a n ) Обратное преобразование Фурье. Самое замечательное, что построенный базис ортогональный, относительно вот такого вот скалярного произведения: (c 1 ... c n )(d 1 ... d n ) = c 1 d 1 + ... + c n d n " width="640"

Таким образом, каждый сигнал (a 1 ... a n ) раскладывается в таком базисе: (a 1 ... a n ) = f 1 b 1 + ... + f n b n ;

• Значит, каждый периодический сигнал имеет два представления: одно - это (a 1 ... a n ), а другое - это (f 1 ... f n ). Переход от одного к другому и есть преобразование Фурье.
• (a 1 ... a n ) - (f 1 ... f n ) Прямое преобразование Фурье.
• (f 1 ... f n ) - (a 1 ... a n ) Обратное преобразование Фурье.
• Самое замечательное, что построенный базис ортогональный, относительно вот такого вот скалярного произведения:
• (c 1 ... c n )(d 1 ... d n ) = c 1 d 1 + ... + c n d n

Преобразование Фурье-разложение функций на синусоиды..

• Виды преобразования Фурье:
• 1. Непериодический непрерывный сигнал можно разложить в интеграл Фурье.
• 2. Периодический непрерывный сигнал можно разложить в бесконечный ряд Фурье.
• 3. Непериодический дискретный сигнал можно разложить в интеграл Фурье.
• 4. Периодический дискретный сигнал можно разложить в конечный ряд Фурье.

Ряд Фурье-матем.послед.

Комплексная запись ряда Фурье

• где   – круговая частота  n -ои гармонической составляющей,   – комплексная амплитуда  n -ой гармоники 
• В этой записи возникают как положительные, так и отрицательные частоты

Ряд Фурье можно записать

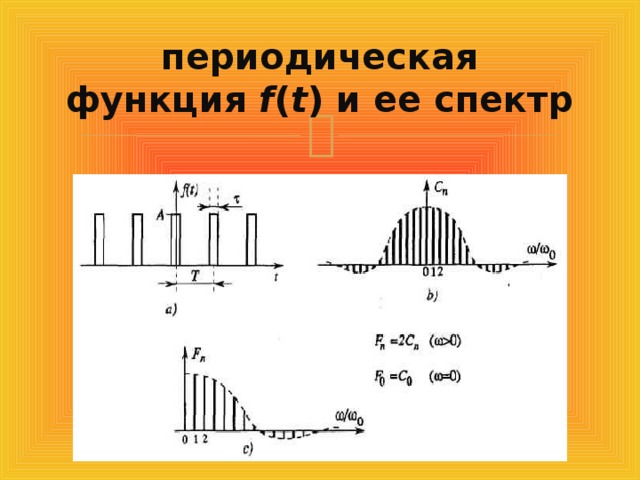
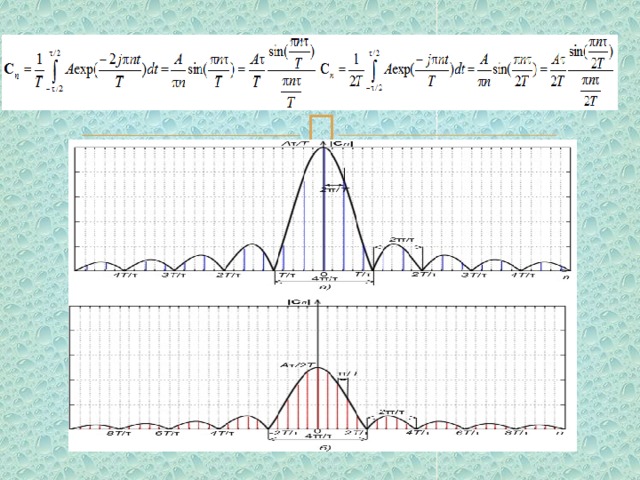
периодическая функция  f ( t ) и ее спектр

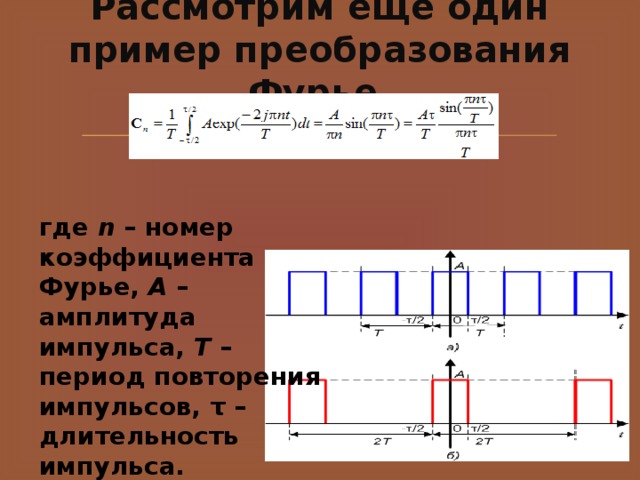
Рассмотрим еще один пример преобразования Фурье.

где  n  – номер коэффициента Фурье,  A  – амплитуда импульса,  T  – период повторения импульсов, τ – длительность импульса.

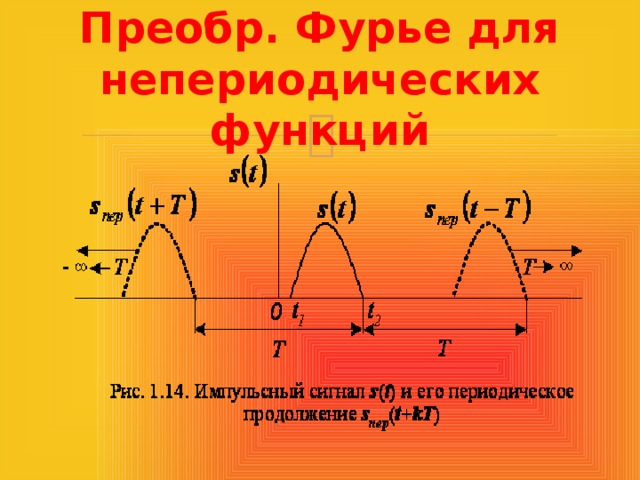
Преобр. Фурье для непериодических функций

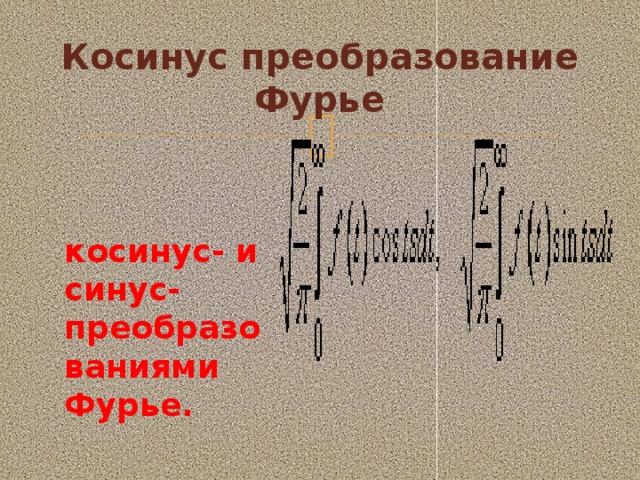
Косинус преобразование Фурье

косинус- и синус-преобразованиями Фурье.

Жан Батист Жозеф Фурье

• Преобразование Фурье вычисляется всякий раз, когда мы слышим звук.
• Преобразование Фурье стало мощным инструментом, применяемым в различных научных областях.
• Интересовался теплотой
• В 1807 французский математик и физик Жан Батист Жозеф Фурье представил во Французский Институт (Institut de France) доклад о синусоидальном представлении температурных распределений.

В чем суть?

• Вернувшись во Францию, Фурье сосредоточился на математических исследованиях, став профессором анализа в Политехнической школе, но в 1802 году вернулся на службу к Наполеону. Фурье был назначен префектом департамента Изер. Пытаясь устранить руины, оставшиеся после революционных событий 1789 года, он возглавил строительство французского участка дороги на Турин и осушил 80 000 км 2 малярийных болот. В этот же период он вывел уравнение, описывающее распространение тепла в твёрдом теле. К 1807 году Фурье изобрёл и метод решения этого уравнения: преобразование Фурье.

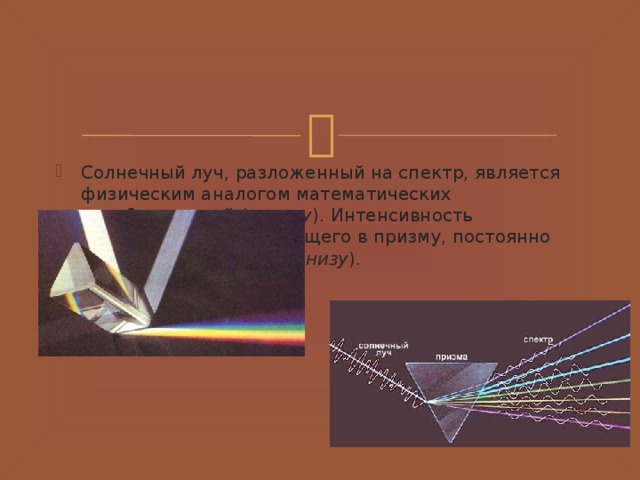
• Солнечный луч, разложенный на спектр, является физическим аналогом математических преобразований ( вверху ). Интенсивность солнечного луча, входящего в призму, постоянно меняется во времени ( внизу ).

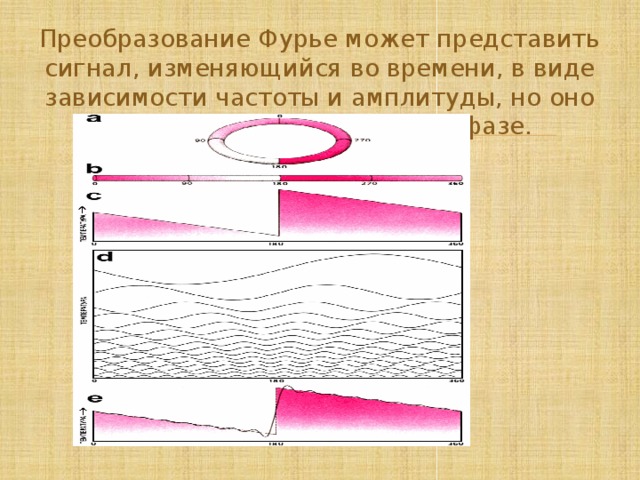
Преобразование Фурье может представить сигнал, изменяющийся во времени, в виде зависимости частоты и амплитуды, но оно даёт также информацию о фазе.

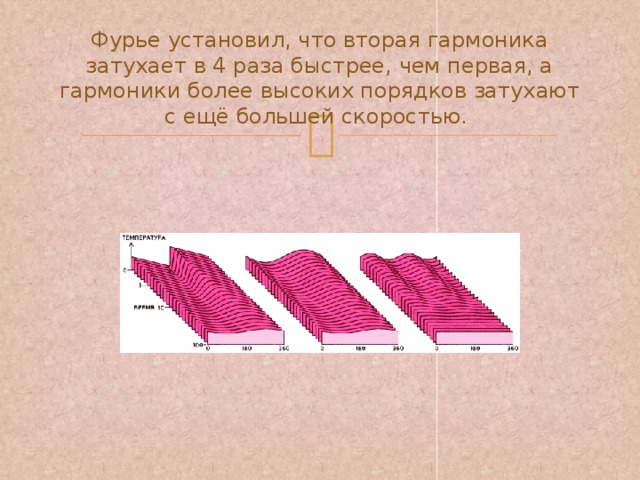
Фурье установил, что вторая гармоника затухает в 4 раза быстрее, чем первая, а гармоники более высоких порядков затухают с ещё большей скоростью.

Лагранж, Лаплас, Лежандр, Био и Пуассон

• Леонард Эйлер также считал идеи Фурье ошибочными, хотя к тому времени сам пришёл к выводу, что некоторые функции можно представить суммой синусоид

Вопрос о сходимости рядов Фурье снова возник в конце XIX века в связи с попытками предсказания интенсивности приливов и отливов.

• Лорд Кельвин

Преобразование Фурье — это функция, представляющая амплитуду и фазу, соответствующие каждой частоте.

• Преобразование можно получить двумя различными математическими методами, один из которых применяется, когда исходная функция непрерывна, а другой — когда она состоит из множества отдельных дискретных измерений.
• Если эта функция получена из значений с определёнными дискретными интервалами, её можно разбить на ряд синусоидальных функций с дискретными частотами — от самой низкой, главной частоты и далее с частотами, вдвое, втрое и т.д. выше главной. Такая сумма синусоид называется рядом Фурье.

Дискретное преобразование Фурье

• Превращает свертку в поточечное изображение

• Набор { f k } и называется дискретным преобразованием Фурье исходного набора { x k }. В качестве точек z k обычно выбирают корни n -й степени из единицы:
• .

• График аналогового сигнала

• Дис.сигнал с част.дис. 1024

• Автокорреляционная функция

Основные свойства ДПФ

• Линейность
• Спектр суммы сигналов равен сумме спектров этих сигналов. Если 
•   то спектр   равен:

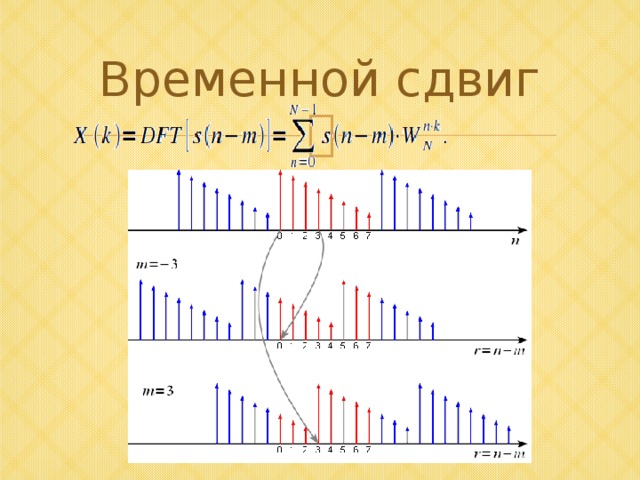
Временной сдвиг

ДПФ циклической свертки сигналов

• Пусть сигнал   есть результат  циклической свертки  сигналов   и   :

Спектр произведения двух сигналов

• Пусть сигнал   равен произведению сигналов    и   , причем   и   - спектры сигналов    и   соответственно.

Свойство частотного сдвига

• Пусть сигнал    имеет спектр  . Произведем циклический сдвиг спектра   и рассмотрим ОДПФ, тогда:

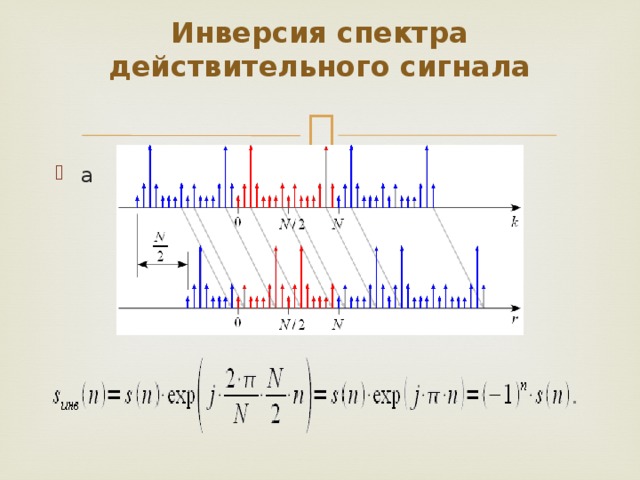
Инверсия спектра действительного сигнала

• а

Свойство двойственности

Дискретные косинус преобразования Фурье.

Матричное представление

• м

Дискретное преобразование Фурье

• Семейство преобразований Фурье (преобразование Фурье, ряды Фурье, дискретные ряды Фурье и дискретное преобразование Фурье)
• Единственный член этого семейства, который имеет отношение к цифровой обработке сигналов, – это дискретное преобразование Фурье (ДПФ), которое оперирует дискретной по времени выборкой периодического сигнала во временной области.
• Фундаментальное уравнение для получения N-точечного ДПФ выглядит следующим образом:

2.1.1 Прямое дискретное преобразование Фурье

• Прямое преобразование:

Обратное дискретное преобразование Фурье

Быстрое преобразование Фурье.

• Основным назначением алгоритма БПФ является разложение сложных негармонических сигналов на несколько гармонических чистых сигналов, частот.

форма двойной спирали ДНК была открыта в 1962 году с использованием дифракции рентгеновских лучей в сочетании с анализом Фурье.

КЕЛЬВИН сказал:

• «Теорема Фурье не только является одним из самых изящных результатов современного анализа , но и дает нам незаменимый инструмент в исследовании самых трудных вопросов современной физики»