Презентация на тему: "ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ"

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

В настоящее время разработано большое число методов численного интегрирования систем дифференциальных уравнений.

К их числу можно отнести метод Рунге-Кутта, явный и неявный методе Эйлера,

метод Милна и т. д.

Однако, несмотря на большое разнообразие этих методов, алгоритм программ для всех их примерно одинаков и состоит из следующих блоков, а именно:

Алгоритм программ

• блока исходных и расчета дополнительных данных;
• блока формирования начальных условий и итерационных циклов;
• блока формирования итерационных уравнений в зависимости от принятого метода численного интегрирования дифференциальных уравнений;
• блока формирования решения дифференциальных уравнений и обработки полученных результатов.

ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ

Основным элементом численных методов является производная функции.

Производная функции - есть предел отношения приращения функции к приращению независимой переменной при стремлении к нулю приращения независимой переменной

При численном нахождении производной заменяют отношение бесконечно малых приращений функций и аргумента

отношением конечных разностей. Очевидно, что чем меньше будет приращение аргумента, тем точнее численное значение производной.

Методы графического представления производной

В основе методов графического представления производной лежит геометрический смысл производной.

Для вычисления первой производной разработаны двухточечные методы численного дифференцирования.

Двухточечные методы

Для двухточечных методов при вычислении производных используется значение функции в двух точках. Приращение аргумента задается тремя способами, откладывая Δ x = h вправо, влево и в обе стороны от исследуемой точки. Соответственно получается три двухточечных метода численного дифференцирования

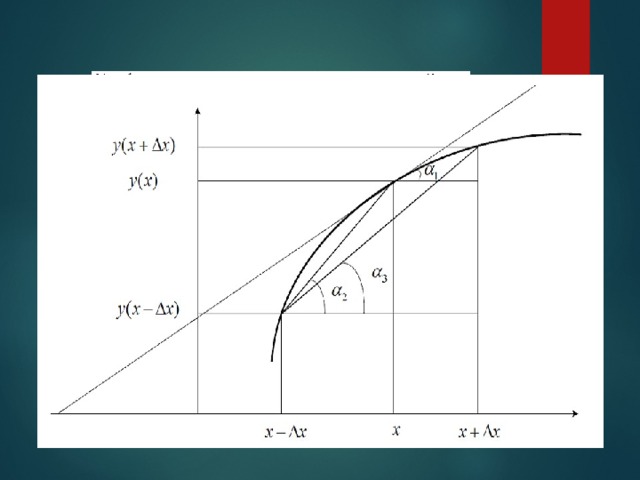
Метод 1

Метод 2

Метод 3

Численное решение дифференциальных уравнений

Дифференциальным уравнением первого порядка называется уравнение вида

или

Функция y ( x ), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.

Метод Эйлера

В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения

c начальными условиями

y 0 =y(x 0 )

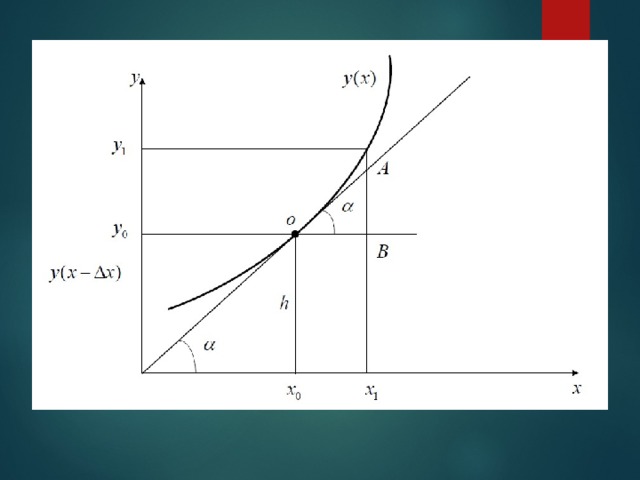
Варианты вывода формул

Существуют аналитический и графический варианты вывода расчетных формул метода Эйлера

Представим это уравнение в виде

Тогда можно записать:

Расчетные формулы 1-го шага

Тогда расчетные формулы для первого шага можно представить в виде:

Расчетные формулы i -го шага

Расчетные формулы i- го шага по аналогии с первым шагом можно записать в виде:

Если обозначить

то расчетные формулы можно записать в виде

Численное решение системы дифференциальных уравнений

Системой дифференциальных уравнений называется система вида

или

где x – независимый аргумент, y i – зависимая функция, y i|x=x0 =y i0 – начальные условия.

Функции y i ( x ), при подстановке которой система уравнений обращается в тождество, называется решением системы дифференциальных уравнений.

Метод Эйлера

Итеррацонные уравнения для численного

решения системы дифференциальных уравнений можно записать в виде:

Математическая модель двигателя постоянного тока

Математическое описания процессов электромеханического преобразования энергии в двигателе постоянного тока (ДПТ) содержит:

• систему уравнений равновесия напряжений, в которых в качестве переменных приняты значения токов в обмотках ОВ и ОЯ;
• уравнение механического равновесия;

• выражение для электромагнитного момента.

В результате определенного вида преобразований получают систему уравнений, описывающую электромеханические процессы в двигателе постоянного тока, в удобном для математического моделирования виде, в форме уравнений Коши:

Система уравнений ДПТ

Для реализации такой модели в среде Mathcad с использованием метода Эйлера 

необходимо:

  сформировать  исходные данные , которые включают в себя параметры двигателя, напряжения ОВ и ОЯ, суммарный момент инерции двигателя и момент статической нагрузки на валу двигателя;

определить и записать начальные условия для исследуемых переменных ДПТ;

определяют число итераций.

Система итерационных уравнений