Определенный интеграл. Формула Ньютона-Лейбница.

Повторение:

• Какая фигура называется криволинейной трапецией?
• Как найти площадь криволинейной трапеции?
• Назовите формулу Ньютона-Лейбница
• Как она связана с формулой площади криволинейной трапеции?

y = f(x)

y = g(x)

Площадь фигуры PDCM ?

y

D

C

M

P

x

b

0

a

A

B

y = f(x)

y = g(x)

Площадь фигуры PMCD ?

y

C

D

A

B

x

b

a

0

P

M

y = x 2

y = x + 2

Пример 1:

вычислить площадь фигуры,

ограниченной линиями y = x 2 , y = x + 2.

y

C

2

B

A

D

O

x

-1

2

y = (x – 2 ) 2

y = 2 √ 8 – x

вычислить площадь фигуры,

ограниченной линиями

y = ( x – 2) 2 , y = 2 √ 8 – x , х = 2, х = 8, у = 0

Пример 2:

y

4

D

B

C

A

4

0

x

8

2

Пример 2:

вычислить площадь фигуры,

ограниченной линиями

y = ( x – 2) 2 , y = 2 √ 8 – x , х = 2, х = 8, у = 0

Определенный интеграл от непрерывной функции y = f ( x ) на отрезке [ a ; b ] обозначается как

Читается как определенный интеграл от a до бэ эф от икс дэ икс.

.(Нижний и верхний пределы). Числа a и b – пределы интегрирования

Геометрический смысл определенного интеграла : Площадь криволинейной трапеции вычисляет по формуле:

Физический смысл определенного интеграла : масса m неоднородного стержня, плотностью ρ=ρ( x ) находящегося на отрезке [ a ; b ] вычисляется по формуле:

Перемещение S материальной точки , движущейся по прямой со скоростью V = V ( t ), за промежуток времени от t = a до t = b , вычисляется по формуле:

Определенный интеграл имеет множество других смыслов, и если хорошо понимать, что это такое, то он нам встречается на каждом шагу.

Теорема. Формула Ньютона – Лейбница.

Если функция y = f ( x ) непрерывна на отрезке [ a ; b ], то справедлива формула

где F ( x ) – первообразная для f ( x ).

Чаще всего встречается вот такая форма записи формулы:

Из теоремы следуют два важных свойства.

Свойство1 . Интеграл от суммы функции равен сумме интегралов функций.

Свойство2 . Постоянный множитель можно вынести за знак интеграла.

Пример. Вычислить определенный интеграл

Решение. Первообразной для служит

Воспользуемся формулой Ньютона – Лейбница

Ответ: 31/5

,

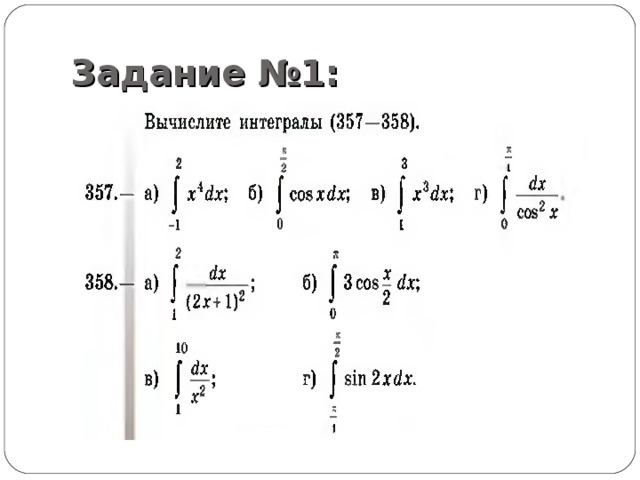
Задание №1:

Пример. Вычислить площадь фигуры, ограниченной функцией y = cos ( x ) на отрезке [0;π/2].

Решение. Давайте построим график косинуса на нашем отрезке

Площадь полученной фигуры вычисляется с помощью определенного интеграла, гда a =0, b = π/2, f ( x )= cos ( x )

Ответ: 1

Пример. Вычислить площадь фигуры, ограниченной линиями

Решение. Давайте построим требуемую фигуру на координатной плоскости.

Вычислим площадь нашей фигуры с помощью определенного интеграла.

Ответ: S=25.6

Задание №2

Задачи для самостоятельного решения.

1.Вычислить определенный интеграл

2. Вычислить площадь фигуры, ограниченной функцией y = sin ( x ) на отрезке [2 π;3π].

3. Вычислить площадь фигуры, ограниченной линиями

Дополнительное задание*:

Домашнее задание:

Образовательная среда, урок 9, задание «Вычислите интеграл»

Давайте обсудим

• Что мы сегодня на уроке повторили, закрепили?

• Чем мы сегодня на уроке занимались?

- Достигли ли мы цели урока?

• Понравился ли тебе урок?
• Какие задания понравились?
• Все ли у тебя получилось?
• Какую оценку ты бы себе поставил за работу на уроке?

Закодированное настроение

• Какие сведения вы храните в своей записной книжке? Как можно назвать записную книжку с точки зрения хранения информации?
• Перечислите достоинства и недостатки хранения информации в оперативной и долговременной памяти.

• Объясните своими словами, что такое носитель информации. Какие носители информации вам известны? Каким носителем информации вы пользуетесь чаще всего?

Спасибо за активную работу на уроке!!!