В презентации представлены: история развития логики, понятие "высказывание", определение "логические операции", задания и т.д.


В презентации представлены: история развития логики, понятие "высказывание", определение "логические операции", задания и т.д.


МАТЕМАТИЧЕСКАЯ ЛОГИКА
Высказывания и операции над ними

Основоположником логики является древнегреческий философ Аристотель . Им были открыты в 338 г. до н.э. три основных закона логики :
Логика Аристотеля на протяжении многих веков дополнялась, усовершенствовалась и развивалась.

В середине XIX в. большой вклад в развитие математической логики внес английский ученый физик Джордж Буль , разработав алгебру высказываний. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
К середине XX в. идеи математической логики проникли в технику, кибернетику, вычислительную математику.
На протяжении изучения математической логики мы будем оперировать различными высказываниями и из всех свойств высказываний нас будет интересовать только одно – ИСТИННО оно или ЛОЖНО .

Высказыванием называется повествовательное предложение, относительного которого можно однозначно сказать, истинно оно или ложно.
Пример:

Не всякое предложение является логическим высказыванием!
Высказываниями НЕ ЯВЛЯЮТСЯ , например, предложения:
«Ученик десятого класса» и «Информатика – интересный предмет» .
Первое предложение ничего не утверждает об ученике,
а второе использует слишком неопределенное понятие «интересный предмет».

Употребляемые в обычной речи слова и словосочетания, такие как
позволяют из уже заданных высказываний строить новые высказывания.
Такие слова и словосочетания называются логическими связками .

Высказывания, образованные из других высказываний с помощью логических связок, называются составными . Высказывания, не являющиеся составными, называются элементарными .
Пример:
из элементарных высказываний « Петров - врач », « Петров - шахматист » при помощи связки « и » можно получить составное высказывание: « Петров врач и шахматист ».
Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний .

Задание 1
Установите, какие из следующих предложений являются логическими высказываниями и определите их истинность:
а) Сириус является спутником Земли.
б) 2 + 3 ≥5.
в) Сегодня отличная погода.
г) Санкт-Петербург расположен на Неве.
д) Музыка Баха слишком сложна.
е) Сумма углов треугольника равна 360 0 .

Для удобства элементарные высказывания будем обозначать через
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
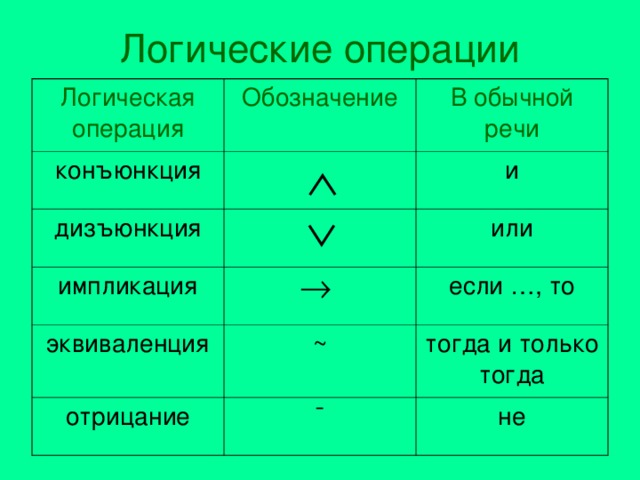
Логические операции
Логическая операция
Обозначение
конъюнкция
В обычной речи
дизъюнкция
и
импликация
или
эквиваленция
отрицание
~
если …, то
тогда и только тогда
¯
не

Конъюнкция
Конъюнкцией двух высказываний А и В называется третье высказывание С, обозначаемое , которое истинно истинны оба высказывания и А и В.
A
B
и
и
и
л
и
л
л
л
и
л
л
л

Дизъюнкция
Дизъюнкцией двух высказываний А и В называется третье высказывание С, обозначаемое ,
которое истинно истинно хотя бы одно из высказываний или А или В.
A
B
и
и
и
л
и
л
л
и
и
л
и
л

Импликация
Импликацией двух высказываний А и В называется третье высказывание С, обозначаемое ,
которое ложно высказывание А – истинно, а В – ложно.
A
B
и
и
и
л
и
л
л
л
и
л
и
и

Эквиваленция
Эквиваленцией двух высказываний А и В называется третье высказывание С, обозначаемое ,
которое истинно А и В имеют одинаковые значения.
A
B
и
и
и
л
и
л
л
л
и
л
л
и
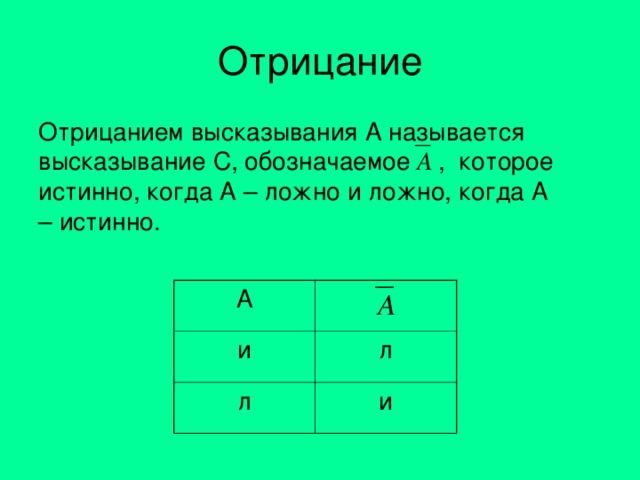
Отрицание
Отрицанием высказывания A называется высказывание С, обозначаемое , которое истинно, когда А – ложно и ложно, когда А – истинно.
A
и
л
л
и

Задание 2
Определите значения истинности следующих высказываний:
а) Кения находится в Африке и в Кирове есть метро.
б) Волк живёт в лесу или в квадрат нельзя вписать окружность.
в) Если 2*2=4, то Киров – столица России.
г) Если 2*2=4 и Киров – столица России, то белые медведи живут в Африке.
д) Мыши едят кошек или мамонты живут в Европе.
е) Если коровы летают, то крокодил умеет плавать.
 7 " width="640"
7 " width="640"
Задание 3
Сформулируйте отрицания следующих высказываний, укажите значения истинности данных высказываний и их отрицаний:
а) 4≤5
б) Не всякое уравнение имеет корень. в) Существуют иррациональные числа.
г) Нет человека, не имеющего матери. д) Неверно, что точка В не лежит на прямой а .
е) 37
 -75%
-75%
 Математическая логика. Высказывания и операции над ними (1.39 MB)
Математическая логика. Высказывания и операции над ними (1.39 MB)
 1
1 1216
1216 78
78 Нравится
0
Нравится
0
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
 Нравится
0
Нравится
0