Тема урока: «Формулы прямоугольников. Формула трапеций. Формула Симпсона.»
Регламент: 90 минут
Цели урока:
- образовательные:
познакомить с понятиями численное интегрирование;
изучить формулы интегрирования: формулы прямоугольников, трапеций, формулу Симпсона;
показать применение формул к решению задач;
формировать умения применять математические знания в практических задачах.
- развивающиеся:
способствовать развитию мыслительных операций: аналогия, систематизация, обобщение, наблюдение;
активизировать деятельность студентов на уроке;
развивать грамотное математическое мышление и культуру речи, умение формулировать свои мысли, пользоваться зрительной и слуховой видами памяти.
- воспитательные:
научиться работать в микрогруппе;
научиться принимать чужую точку зрения и отстаивать свою;
научиться слушать своих товарищей;
научиться защищать решение задачи.
Вид урока: лекция с элементами беседы, с работой на ИД.
Тип урока: урок изучения нового материала.
Технологии обучения: информационно-коммуникационная, проблемного обучения, развивающего обучения, здоровье сберегающая.
Обеспечение урока:
- техническое:
ноутбук, интерактивная доска, проектор, презентация «Численные методы»
- учебно-методическое:
Учебник: Омельченко В.П. Математика: учебное пособие для СПО, лекционный материал к уроку.
ХОД УРОКА
1. Актуализация ранее усвоенных знаний:
Сообщение темы и цели урока.
1.1. Проверка домашнего задания (фронтальная проверка, выборочно проверить в тетрадях).
2. Изучение нового материала: (методы, используемые при изучении: объяснительно – иллюстративный метод, демонстрационный; работа с литературой; фронтальная и индивидуальная работа с обучающимися).
2.1. Формулы прямоугольников. Формула трапеций. Формула Симпсона. Рассказ преподавателя с использованием интерактивной доски.
Основная задача дифференциального исчисления заключается в следующем: дана функция 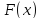 , требуется найти ее производную. При этом если производная существует в каждой точке
, требуется найти ее производную. При этом если производная существует в каждой точке 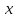 некоторого промежутка
некоторого промежутка 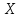 , то это также некоторая функция
, то это также некоторая функция 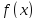 на
на 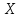 такая, что
такая, что 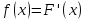 . Однако часто приходится решать и обратную задачу. Для решения обратной задачи служит операция интегрирования.
. Однако часто приходится решать и обратную задачу. Для решения обратной задачи служит операция интегрирования.
2.2. Самостоятельная работа с учебной литературой стр. 230 – 250. Конспектирование в тетрадь по группам:
1. Работает над формулой приближенного интегрирования - формулой прямоугольников;
2. Работает над формулой приближенного интегрирования – формулой трапеций;
3. Работает над формулой приближенного интегрирования – формулой параболических трапеций (формула Симпсона). Составить математическую модель прикладной задачи.
3. Закрепление изученного материала: (формы на данном этапе: фронтальная и индивидуальная работа; методы: наглядный, частично- поисковый, проблемный).
3.1. Фронтальная беседа с обучающимися. Обобщить этапы изучения темы.
3.2. Решение задач.
Все три группы одновременно вычисляют интеграл:
Пример 1
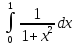 =
= 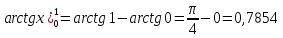 .
.
Блок 1
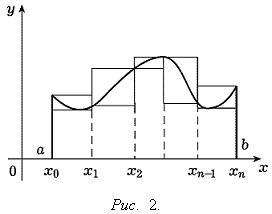
Разделим интервал интегрирования 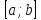 на
на 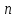 равных частей (частичных интервалов) и заменим данную трапецию ступенчатой фигурой, состоящей из
равных частей (частичных интервалов) и заменим данную трапецию ступенчатой фигурой, состоящей из 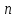 прямоугольников, опирающихся на частичные интервалы, причем высоты этих прямоугольников равны значениям функции
прямоугольников, опирающихся на частичные интервалы, причем высоты этих прямоугольников равны значениям функции 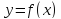 в начальных или конечных точках частичных интервалов. Значение площади этой фигуры и будет давать приближенное значение искомого интеграла
в начальных или конечных точках частичных интервалов. Значение площади этой фигуры и будет давать приближенное значение искомого интеграла 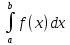 .
.
Если обозначить значения функции 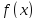 в точках деления через
в точках деления через 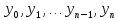 , то будем иметь следующую формулу - формулу прямоугольников :
, то будем иметь следующую формулу - формулу прямоугольников :
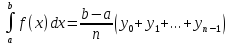 или
или 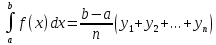
Блок 2
Оставим разбиение интервала 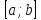 прежним, но заменим теперь каждую дугу линии
прежним, но заменим теперь каждую дугу линии 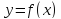 , соответствующую частичному интервалу . хордой, соединяющей конечные точки этой дуги. Таким образом, заменяем данную криволинейную трапецию
, соответствующую частичному интервалу . хордой, соединяющей конечные точки этой дуги. Таким образом, заменяем данную криволинейную трапецию 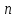 прямолинейными. Площадь каждой трапеции, построенной на частичном интервале, равна полу сумме площадей, соответствующих этому интервалу прямоугольников. Суммируя все эти площади, получим формулу трапеций:
прямолинейными. Площадь каждой трапеции, построенной на частичном интервале, равна полу сумме площадей, соответствующих этому интервалу прямоугольников. Суммируя все эти площади, получим формулу трапеций:
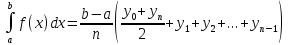
Блок 3
Разобьем интервал 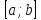 на
на 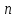 равных частей , но предположим, что
равных частей , но предположим, что 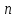 – четное число:
– четное число: . Заменим дугу линии
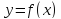 , соответствующую интервалу
, соответствующую интервалу , дугой параболы, ось которой параллельна оси ординат и которая проходит через следующие три точки дуги: начальную точку дуги
, среднюю точку
, конечную точку
. Площадь данной трапеции приближенно равна сумме площадей получающихся параболических трапеций и выражается формулой:
1 группа
Решает пример 1 по формуле прямоугольников : при
Таблица расчетов:
| | 0 | 1 | 2 | 3 | 4 | 5 |
| | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
| | 1 | 0,9615 | 0,8621 | 0,7353 | 0,6098 | 0,5 |
2 группа Решает пример 1 по формуле трапеций : при
Таблица расчетов:
| | 0 | 1 | 2 | 3 | 4 | 5 |
| | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
| | 1 | 0,9615 | 0,8621 | 0,7353 | 0,6098 | 0,5 |
3 группа Решает пример 1 по формуле параболических трапеций : при
Таблица расчетов:
| | 0 | 1 | 2 | 3 | 4 |
| | 0 | | | | |
| | 1 | | | |
|
Занесем итоги расчета в таблицу и сравним:
|
| значение интеграла | абсолютная погрешность | относительная погрешность |
| формула Н-Л | 0,7854 |
|
|
| фор-ла прям-ков | 0,8337 | | 6,1 % |
| фор-ла трапеций | 0,7837 | | |
| фор-ла Симпсона | 0,7854 | 0 | 0 |
= 6,1 %
Пример 2
Вычислить определенный интеграл по формуле Симпсона с точностью до 0,0001
1 группа вычисляет интеграл при
Вычислить шаг :
Расчетная таблица:
| | 0 | 1 | 2 |
| | -0,8 | -0,4 | 0 |
| | 0,61172 | 0,57833 | 0,57735 |
2 группа вычисляет интеграл при
Вычислить шаг :
Расчетная таблица:
| | 0 | 1 | 2 | 3 | 4 |
| | -0,8 | -0,6 | -0,4 | -0,2 | 0 |
| | 0,611724 | 0,584981 | 0,578338 | 0,577381 | 0,57735 |
Оценим погрешность : =
3 группа
Вычислить шаг :
Расчетная таблица:
| | | | | | |
| 0 | -0,8 | 0,611724 | 5 | -0,3 | 0,577584 |
| 1 | -0,7 | 0,594236 | 6 | -0,2 | 0,577381 |
| 2 | -0,6 | 0.584981 | 7 | -0,1 | 0,577351 |
| 3 | -0,5 | 0,589381 | 8 | 0 | 0,577350 |
| 4 | -0,4 | 0,578338 |
|
|
|
Оценим погрешность:
=
Полученная оценка погрешности меньше, чем требуемая точность.
Формула Симпсона дает практически точное вычисление определенного интеграла.
Приведенные правила численного интегрирования помогают решать прикладные задачи.
Прикладная задача
Ширина реки равна 20м; промеры глубины в некотором поперечном ее сечении через каждые 2м дали следующую таблицу:
|
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| | 0.2 | 0,5 | 0,9 | 1,1 | 1,3 | 1,7 | 2,1 | 1,5 | 1,1 | 0,6 | 0,2 |
Расстояние (в метрах) от одного из берегов обозначено через 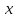 , соответствующая глубина реки ( также в метрах) – через
, соответствующая глубина реки ( также в метрах) – через Требуется найти площадь
поперечного сечения реки.
По формуле Симпсона находим:
4. Итог урока. Оценка деятельности (выставление оценок, оценка работы обучающихся).
5. Домашнее задание: Гл.3, П.1.1-1.3, Стр. 230-250, пример 3.6.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект урока из раздела "Численное дифференцирование и интегрирование" (51.75 KB)
Конспект урока из раздела "Численное дифференцирование и интегрирование" (51.75 KB)
 0
0 712
712 69
69 Нравится
0
Нравится
0


