ЕГЭ профильный уровень: задание 10. Формулы и функции

Задание 10 (ЕГЭ профильный уровень).

Формулы и функции.

Все задания делятся на три большие категории в порядке возрастания сложности:

1. Функции;

2. Формулы;

3. Комбинированные.

Работа с формулами

Если в задание дано уравнение, которое содержит несколько переменных, ни одна из которых не рассматривается как «основная» — перед нами задача на работу с формулами. Например:

Как видно, формулы могут связывать по три, а то и по четыре переменных. Но решаются такие задачи всегда одинаково: значения переменных, входящих в формулу, указаны прямо в тексте. За исключением одной — ее-то и требуется найти. Таким образом, решение задания с формулой состоит из трех шагов:

1. Найти и выписать из текста все известные переменные. Не забудьте перевести все в единую систему измерений. Если одна величина указана в км/ч, а другая — в м/с, то все надо перевести в м/с.

2. Подставить эти переменные в формулу. Получится уравнение с одной неизвестной.

3. Решить полученное уравнение — получим ответ.

Прежде чем решать задание, постарайтесь преобразовать исходную формулу в максимально простой вид — избавляйтесь от корней, дробей и т.д.

Задача 1. В электросеть включен предохранитель, рассчитанный на силу тока 20 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Сила тока в цепи I связана с напряжением U соотношением: , где R — сопротивление прибора. Ответ выразите в Омах.

Решение:

Для начала перепишем формулу: U = I · R. По условию, нам известно напряжение U = 220 В и сила тока I = 20 А. Ничего переводить в другую систему счисления не надо — все и так переведено. Поэтому находим R:

220=20R;
R = 11.

Ответ: 11

Задача 2. Если наблюдатель находится на небольшой высоте h над поверхностью Земли, то расстояние от него до линии горизонта можно найти по формуле: , где R = 6400 км — радиус Земли. Найдите наименьшую высоту, с которой должен смотреть наблюдатель, чтобы он видел линию горизонта на расстоянии не менее 6,4 км. Ответ выразите в метрах.

Решение

Перепишем формулу: l² = 2Rh. Поскольку нам известны две величины  l = 6,4 км и R = 6400 км — и обе выражены в километрах, можно подставить в формулу и найти h:

6,4²=2·6400h;
40,96=12800·h;
h = 0,0032.

Итак, h = 0,0032 км. Но ответ просят дать в метрах. В одном километре 1000 метров, поэтому имеем:

h = 0,0032 · 1000 = 3,2 м.

Ответ: 3,2

Задача 3. Коэффициент полезного действия некоторого двигателя определяется по формуле:

. При каком наименьшем значении температуры нагревателя T₁ КПД этого двигателя будет не меньше 70%, если температура холодильника T₂ = 150?

Решение

Перепишем формулу, избавившись от дроби: η · T₁ = (T₁ − T₂) · 100. В этой формуле известны КПД η = 70 и температура холодильника T₂ = 150. Подставляем — получаем уравнение относительно T₁:

70·T₁=(T₁−150)·100;
70·T₁=100·T₁−15000;
−30·T₁=−15000;
T₁ = 500.

Ответ: 500

Задача 4. В розетку электросети подключены приборы, общее сопротивление которых составляет 60 Ом. Параллельно с ними в розетку хотят подключить обогреватель. Определите наименьшее допустимое сопротивление этого обогревателя, если для нормального функционирования электросети общее сопротивление в ней должно быть не менее 10 Ом. При этом известно, что при параллельном соединении двух проводников с сопротивлениями R₁ и R₂ их общее сопротивление определяется по формуле: .

Решение

Преобразуем формулу, избавившись от дроби: R · (R₁ + R₂) = R₁ · R₂.

Общее сопротивление должно быть не менее 10 Ом — значит, R = 10. Что касается R₁ и R₂, то положим R₁ = 60. Соответственно, R₂ — сопротивление обогревателя, которое требуется найти. Имеем:

10 · (60 + R₂) = 60 · R₂;
600 + 10 · R₂ = 60 · R₂;
50 · R₂ = 600;
R₂ = 12.

Ответ: 12

Задача 5. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 30 см. Расстояние d₁ от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d₂ от линзы до экрана — в пределах от 180 до 210 см. Изображения на экране будет четким, если выполнено соотношение: 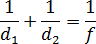. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было четким. Ответ выразите в сантиметрах.

Решение

Перепишем формулу, избавившись от дробей:
f · (d₁ + d₂) = d₁ · d₂.

Нам нужно найти d₁. При этом значение f = 30, а d₂ изменяется от 180 до 210. Получим два уравнения:

30 · (d₁ + 180) = d₁ · 180; 30 · (d₁ + 210) = d₁ · 210;
30 · d₁ + 5400 = 180 · d₁; ... (решается аналогично предыдущему)
150 · d₁ = 5400; d₁ = 35.
d₁ = 36.

По условию, оба значения d₁ допустимы, поэтому выбираем наименьшее: d₁ = 35.

Ответ: 35

Задание, сводящиеся к линейным уравнениям

Линейные уравнения — простейшие конструкции, которые изучаются в школьном курсе математики. Многие задания 10, которые встречаются в ЕГЭ и выглядят достаточно "угрожающе", в итоге сводятся к  линейным уравнениям.

Линейные уравнения возникают, если:

1. При подстановке переменных в исходную формулу задачи сводится к пропорции. В этом случае достаточно вспомнить основное свойство пропорции — умножение «крест-накрест» — и мы получим классическое линейное уравнение;

2. Формула изначально была линейной, записываем уравнение, решаем, находим ответ.

В любом случае, помните основное правило, одинаково полезное для решения всех заданий 10:

Избавляйтесь от дробей и отрицательных степеней в формулах. Если можно умножить — умножайте; можно сократить — сокращайте. Дроби (особенно десятичные) можно записывать только в ответе.

Задача 6. Некоторая компания продает свою продукцию по цене p = 700 руб. за единицу, переменные затраты на производство одной единицы продукции составляют v = 400 руб., постоянные расходы предприятия f = 800 000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле: π (q) = q(p − v) − f. Определите наименьший месячный объем производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 1 000 000 руб.

Решение

По условию, нам известно следующее:

π (q) = q(p − v) − f; p = 700; v = 400; f = 800 000.

Требуется, чтобы месячная операционная прибыль π (q) = 1 000 000. Подставляем значения переменных p, v и f в формулу и решаем уравнение:

1 000 000 = q(700 − 400) − 800 000;
1 000 000 + 800 000 = q · 300;
300q = 1 800 000;
q = 6000.

Ответ: 6000

Задача 7. Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: , где U — напряжение в вольтах, R — сопротивление электроприбора в Омах. В электросеть включен предохранитель, который плавится, если сила тока превышает 11 А. Определите, какое минимальное сопротивление (в Омах) должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать.

Решение

Избавимся от дробей в формуле, переписав ее в виде I · R = U. Далее подставим в эту формулу известные величины: силу тока I = 11 и напряжение U = 220 (единицы измерения писать не надо). Имеем:

11 · R = 220 ⇒ R = 20.

Ответ: 20

Задача 8. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой: , где T₁ — температура нагревателя (в градусах Кельвина), T₂ — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя T₁ КПД этого двигателя будет не меньше 35%, если температура холодильника T₂ = 260 К? Ответ выразите в градусах Кельвина.

Решение

Избавляемся от дроби в формуле. Получим:

η · T₁ = (T₁ − T₂) · 100%

Нам известны КПД двигателя η = 35 и температура холодильника T₂ = 260. Единицы измерения писать не надо, т.к. по условию все числа уже приведены в СИ.

35 · T₁ = (T₁ − 260) · 100;
35T₁ = 100T₁ − 26 000 — раскрыли скобки;
26 000 = 100T₁ − 35T₁;
26 000 = 65T₁;
T₁ = 400

Ответ: 400

Задача 9. При температуре 0 °C рельс имеет длину l₀ = 15 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону: l(t°) = l₀(1 + α · t°), где α = 1,2 · 10⁻⁵ (°C)⁻¹ — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 6,3 мм? Ответ выразите в градусах Цельсия.

Решение

Для начала выясним, что означает фраза «рельс удлинится на 6,3 мм». Итак, был рельс длиной 15 метров. Затем рельс удлинился на 6,3 мм = 6,3 · 10⁻³ метра (т.к. 1 мм — это 10⁻³ метра), и теперь общая длина равна 15 + 6,3 · 10⁻³ метра.

Имеем: l₀ = 15; l(t°) = 15 + 6,3 · 10⁻³; α = 1,2 · 10⁻⁵. Подставляем в исходную формулу — получаем:

15 + 6,3 · 10⁻³ = 15 · (1 + 1,2 · 10⁻⁵ · t);
15 + 6,3 · 10⁻³ = 15 + 15 · 1,2 · 10⁻⁵ · t — раскрыли скобки;
6,3 · 10⁻³ = 18 · 10⁻⁵ · t — убрали 15 с обеих сторон;
6,3 · 10⁻³ · 10⁵ = 18 · 10⁻⁵ · 10⁵ · t — умножили все на 10⁵;
6,3 · 10² = 18 · t — избавились от отрицательных степеней;
18t = 630 — получили нормальное уравнение;
t = 35

Ответ: 35

Комбинированные задания

Часто бывает, что в одном задании10 присутствует и функция, и формула. В таких заданиях кроме основной переменной присутствуют дополнительные неизвестные, значения которых надо искать где-то в тексте.

Общая схема решения почти ничем не отличается от задач с формулами: найти в тексте числа и подставить их в исходную формулу. Если все сделать правильно, получится стандартное уравнение с одной переменной.

Задача 10. В ходе распада радиоактивного изотопа его масса уменьшается по закону: , где m₀ (мг) — начальная масса изотопа, t (мин) — время, прошедшее от начального момента, T (мин) — период полураспада. В начальный момент времени масса изотопа m₀ = 56 мг. Период его полураспада T = 7 мин. Через сколько минут масса изотопа будет равна 7 мг?

Решение

По условию, известны следующие величины: m₀ = 56; T = 7. Подставим их в функцию — получим m(t) = 56 · 2^−t/7. Требуется найти момент, когда m(t) = 7 мг. Составим и решим уравнение:

56 · 2^−t/7 = 7;
2^−t/7 = 1/8 — разделили все на 56;
2^−t/7 = 2⁻³ — представили 1/8 как 2⁻³;
−t/7 = −3;
t = 21.

Ответ: 21

Задача 11. Для одного из предприятий-монополистов зависимость объема спроса на продукцию q (единиц в месяц) от ее цены p (тыс. руб.) задается формулой: q = 75 − 5p. Определите максимальный уровень p цены (в тыс. руб.), при котором значение выручки предприятия за месяц r = q · p составит не менее 270 тыс. руб.

Решение

Итак, у нас есть функция r = q · p, причем q — неизвестная величина. Более того, переменная q сама является функцией: по условию, q = 75 − 5p. Подставим это выражение в функцию r. Получим:

r = (75 − 5p) · p = 75p − 5p².

Теперь у нас есть функция, выражающая прибыль через цену. Все цены установлены в тысячах рублей — это следует из условия. Также, по условию, прибыль должна быть не менее 270 тыс. руб., поэтому можно написать r = 270. Составим и решим уравнение:

270 = 75p − 5p²;
5p² − 75p + 270 = 0 — перенесли все влево;
p² − 15p + 54 = 0 — разделили все на 5;
... (решаем квадратное уравнение)
p₁ = 6; p₂ = 9.

Поскольку нас интересует наибольшая цена, выбираем p₂ = 9.

Ответ: 9

Задача12. При температуре 0 °С рельс имеет длину l₀ = 20 метров. При прокладке путей между рельсами оставили зазор в 9 мм. При возрастании температуры будет происходить тепловое расширение рельса, и его длина будет меняться по закону l(t) = l₀ · (1 + a · t), где a = 1,2 · 10⁻⁵ (°C)⁻¹ — коэффициент теплового расширения, t — температура (в градусах Цельсия). При какой минимальной температуре зазор между рельсами исчезнет? Ответ выразите в градусах Цельсия.

Решение

Изначально нам известны две величины: l₀ = 20 и a = 1,2 · 10⁻⁵. Самый тонкий момент — понять, чему равно l(t). А именно: зазор исчезнет, когда рельс удлинится на эти самые 9 мм. Была длина 20 метров, а стала — 20 метров + 9 мм.

Переведем все в метрическую систему. В одном метре 1000 мм, поэтому 9 мм = 9 · 10⁻³ м. Итого, l(t) = 20 + 9 · 10⁻³. Оставим эту запись именно в таком виде, не будем складывать. Получилось уравнение:

20 + 9 · 10⁻³ = 20 · (1 + 1,2 · 10⁻⁵ · t).

Раскроем скобки — и после очевидных преобразований уравнение станет совсем простым:

20 + 9 · 10⁻³ = 20 + 20 · 1,2 · 10⁻⁵ · t;
9 · 10⁻³ = 24 · 10⁻⁵ · t — убрали с обеих сторон число 20.

Умножим обе стороны на 10⁵ и получим:

9 · 10^{−3 + 5} = 24 · 10^{−5 + 5} · t;
9 · 10² = 24t — обычное линейное уравнение;
t = 900/24 = 37,5.

Ответ: 37,5

Общие выводы из приведенных решений:

1. Иногда в задачах о радиоактивных изотопах указывают название вещества — не обращайте внимания на это. Хоть медь-64, хоть ксенон-133 — что угодно. Эти числа не участвуют в решении, а только засоряют текст задачи.

2. В задачах о предприятиях-монополистах не стоит пугаться единиц измерений. Даже если это сотни тысяч рублей, не надо приписывать нули к указанным в задаче числам.

3. Когда речь идет о рельсах, важно понимать, что l(t) — это длина всего рельса, а не только его удлинение. Само удлинение (или зазор) надо перевести в метры. Например, 4,5 мм — это 4,5 · 10⁻³ м. Кроме того, не спешите складывать длину рельса и зазор. Лучше раскройте скобки — формула сложная, но объем вычислений сократится многократно. И не надо вычислять 10⁻⁵, а то получится одна стотысячная и будет очень грустно.

Сложные задания

Существуют еще более сложные задачи, требующие действительно грамотных размышлений.

Задача 13. Для определения эффективной температуры звезд используют закон Стефана — Больцмана, согласно которому мощность излучения нагретого тела прямо пропорциональна площади его поверхности и четвертой степени температуры: , где σ = 5,7 · 10⁻⁸ — постоянная, площадь измеряется в квадратных метрах, температура — в градусах Кельвина, а мощность — в ваттах. Известно, что некоторая звезда имеет площадь S = (1/128) · 10²⁰ м², а излучаемая ею мощность P не менее 1,14 · 10²⁵ Вт. Определите наименьшую возможную температуру этой звезды. Ответ дайте в градусах Кельвина.

Решение

Нам известна мощность P, площадь S и постоянная σ. Подставим их в формулу — получим:

1,14 · 10²⁵ = 5,7 · 10⁻⁸ · (1/128) · 10²⁰ · T ⁴.

Единицы измерения не пишем — они только засоряют уравнение. Чтобы упростить решение, умножим обе стороны на 128, а затем по возможности сократим количество множителей. Имеем:

1,14 · 10²⁵ · 128 = 5,7 · 10⁻⁸ · (1/128) · 10²⁰ · T ⁴ · 128;
1,14 · 128 · 10²⁵ = 5,7 · 10⁻⁸ · 10²⁰ · T ⁴ — сократили множители, отмеченные красным;
1,14 · 128 · 10²⁵ = 5,7 · 10¹² · T ⁴;
1,14 · 128 · 10^{25 − 12} = 5,7 · 10^{12 − 12} · T ⁴ — разделили все на 10¹²;
1,14 · 128 · 10¹³ = 5,7 · T ⁴;
1,14 · 128 · 10¹³ : 5,7 = 5,7 · T ⁴ : 5,7 — делим все на 5,7;
0,2 · 128 · 10¹³ = T ⁴ — потому что 1,14 : 5,7 = 0,2;
2 · 10⁻¹ · 128 · 10¹³ = T ⁴ — записали 0,2 = 2 · 10⁻¹;
256 · 10¹² = T ⁴ — группируем двойки и десятки;
T ⁴ = 10¹² · 2⁸ — поскольку 256 = 2⁸;
T = 10³ · 2² = 1000 · 4 = 4000..

Действительных корней в уравнении будет два: T₁ = 4000 и T₂ = −4000. Но температура в Кельвинах не может быть отрицательной, поэтому второй вариант нас не интересует.

Ответ: 4000

Задача 14. В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону: , где t — время в секундах, прошедшее с момента открытия крана, H₀ = 20 м — начальная высота столба воды, k = 1/50 — отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения (считайте g = 10 м/с²). Через сколько секунд после открытия крана в баке останется четверть первоначального объема воды?

Решение

Для начала выясним, чему равно искомое H(t). По условию, в баке должна остаться четверть первоначального объема воды. Поэтому H(t) = (1/4) · 20 = 5 м.

Теперь, когда все параметры известны, подставим числа в функцию. Чтобы не усложнять выкладки, заметим следующее:

Таким образом, вместо корня можно смело писать число 20. Имеем:

5 = 20 − 20 · (1/50) · t + (10/2) · (1/50)² · t²;
0 = 15 − 20 · (1/50) · t + 5 · (1/50)² · t² — перенесли все в одну сторону;
(1/50)² · t² − 4 · (1/50) · t + 3 = 0 — разделили все на 5.

Сделаем замену переменной: (1/50) · t = x. Тогда (1/50)² · t² = x², и все уравнение перепишется следующим образом:

x² − 4x + 3 = 0;
(x − 3) · (x − 1) = 0 — корни квадратного уравнения легко угадываются без всякого дискриминанта;
x₁ = 3; x₂ = 1.

Теперь вспоминаем, что такое x. Поскольку мы выполняли замену x = (1/50) · t, имеем:

t = 50x;
t₁ = 50 · 3 = 150;
t₂ = 50 · 1 = 50.

Итак, у нас два ответа: числа 50 и 150. Заметим, что в момент времени t = 100 высота столба воды равна:

H(100) = 20 − 20 · (1/50) · 100 + 5 · (1/50)² · 100² = 20 − 40 + 20 = 0.

Другими словами, через t = 100 секунд вода полностью вытечет из бака, и уравнение H(t) теряет физический смысл. Поэтому вариант t = 150 нас не интересует. Остается только t = 50.

Ответ: 50

Типичные задания с функциями

Говоря простым языком, функции — это когда одна переменная зависит от другой. В заданиях функции всегда задаются формулами и обозначаются разными буквами: f(x), h(t), m(t)...

1. Найти в тексте задачи, чему должна быть равна функция. Пусть это будет число K.

2. Решить уравнение f(x) = K. Ну, или h(t) = K — в зависимости от того, как называется функция.

3. Если корень один — это и есть ответ. Если корней два и более — надо немного подумать. Например, время не может быть отрицательным, масса — нулевой, и так далее.

Задача 15. Высота, на которой находится камень, брошенный с земли вертикально вверх, меняется по закону h(t) = 2 + 12t − 5t², где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд камень будет находиться на высоте более 6 метров?

Решение

Из условия следует, что надо решить уравнение h(t) = 6. Получаем обычное квадратное уравнение:

2 + 12t − 5t² = 6;
5t² − 12t + 4 = 0 — собрали все с одной стороны;
... (решаем обычное квадратное уравнение)
t₁ = 0,4; t₂ = 2.

Итак, у нас два корня. Что это значит? В момент времени t₁ = 0,4 камень был на высоте 6 метров, затем — очевидно, больше 6, и, наконец, в момент t₂ = 2 снова 6 метров. Короче говоря, в период с t₁ = 0,4 до t₂ = 2 камень находился на высоте более 6 метров. Найдем длину отрезка:

l = t₂ − t₁ = 2 − 0,4 = 1,6.

Ответ: 1,6

Задача 16. Камень брошен вниз с высоты 24 метра. Пока камень не упал, его высоту можно находить по формуле h(t) = 24 − 7t − 5t², где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд камень будет падать?

Решение

Что значит, что камень упал? Это означает, что его высота над поверхностью земли стала равна нулю. Итак, надо решить уравнение h(t) = 0. Имеем:

24 − 7t − 5t² = 0 — обычное квадратное уравнение;
... (решаем квадратное уравнение)
t₁ = 1,6; t₂ = −3;

Очевидно, корень t₁ = −3 нам не подходит, поскольку время не может быть отрицательным. Поэтому камень будет падать 1,6 секунды.

Ответ: 1,6

Задача 17. В боковой стенке цилиндрического бака вблизи дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем меняется по закону: H(t) = 5 − 1,6t + 0,128t², где t — время в минутах. В течение какого времени вода будет вытекать из бака?

Решение

Вода будет вытекать из бака до тех пор, пока высота столба не станет равной нулю. Поэтому H(t) = 0. Подставляем это значение в функцию и решаем уравнение:

0 = 5 − 1,6t + 0,128t²;
0 = 625 − 200t + 16t² — умножили все на 125;
16t² − 200t + 625 = 0 — стандартное квадратное уравнение;

D = b² − 4ac = (−200)² − 4 · 16 · 625 = 40 000 − 40 000 = 0 — уравнение имеет ровно 1 корень.
t = −b : (2a) = −(−200) : (2 · 16) = 200 : 32 = 6,25.

Таким образом, вода перестанет вытекать из бака через 6,25 минуты.

Ответ: 6,25

Задача 18. После дождя уровень воды в колодце может повыситься. Мальчик определяет его, измеряя время падения t небольших камушков в колодец и рассчитывая по формуле h = −5t², где t измеряется в секундах, а h — в метрах. До дождя время падения камушков составляло 1,4 секунды. На какую минимальную высоту должен подняться уровень воды после дождя, чтобы измеряемое время изменилось больше чем на 0,1 секунды? Ответ выразите в метрах.

Решение

Это немного нестандартная задача с функцией. По условию, аргумент t может принимать 2 значения:

t₁ = 1,4 — исходное, дано в условии задачи;
t₂ = 1,4 − 0,1 = 1,3 — новое значение.

Теперь подставим эти значения в функцию h(t). Так мы найдем расстояние от верхней кромки колодца до поверхности воды до и после дождя. Имеем:

h(t₁) = −5 · (1,4)² = ... = −9,8;
h(t₂) = −5 · (1,3)² = ... = −8,45.

Итак, есть два значения: −9,8 метра и −8,45 метра. Если вычесть из большей высоты меньшую, получим искомую минимальную высоту Δh, на которую должен подняться уровень воды:

Δh = −8,45 − (−9,8) = 9,8 − 8,45 = 1,35

Ответ: 1,35

Самостоятельная работа

1 вариант

Начало формы

1. Зависимость объема спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задается формулой: q = 160 − 10p. Выручка предприятия за месяц r (тыс. руб.) задается формулой r(p) = q · p. Определите наибольшую цену p, при которой месячная выручка r(p) составит не менее 600 тыс. руб. Ответ приведите в тыс. руб.

2. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур дается выражением: T(t) = T₀ + bt + at², где T₀ = 1350 К, a = −15 К/мин, b = 180 К/мин². Известно, что при температуре нагревателя свыше 1650 К прибор может испортиться, поэтому его нужно отключать. Определите (в минутах), через какое наибольшее время после начала работы нужно отключать прибор.

3. Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: , где U — напряжение в вольтах, R — сопротивление электроприбора в Омах. В электросеть включен предохранитель, который плавится, если сила тока превышает 20 А. Определите, какое минимальное сопротивление (в Омах) должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать.

4. После дождя уровень воды в колодце может повыситься. Мальчик определяет его, измеряя время падения t небольших камушков в колодец и рассчитывая по формуле: h = −5t², где t измеряется в секундах, а h — в метрах. До дождя время падения камушков составляло 0,8 секунды. На какую минимальную высоту должен подняться уровень воды после дождя, чтобы измеряемое время изменилось больше чем на 0,2 секунды? Ответ выразите в метрах.

5. В ходе распада радиоактивного изотопа его масса уменьшается по закону: , где m₀ (мг) — начальная масса изотопа, t (мин) — время, прошедшее от начального момента, T (мин) — период полураспада. В лаборатории получили вещество, содержащее в начальный момент времени m₀ = 200 мг изотопа меди, период полураспада которого T = 2 мин. В течение скольких минут масса изотопа будет не меньше 12,5 мг?

6. Высота над землей подброшенного вверх мяча меняется по закону: h(t) = 1 + 11t − 5t², где t измеряется в секундах, а h — в метрах. Сколько секунд мяч будет находиться на высоте более трех метров?

7. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой: , где T₁ — температура нагревателя (в градусах Кельвина), T₂ — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя T₁ КПД этого двигателя будет не менее 75%, если температура холодильника T₂ = 280 К? Ответ выразите в градусах Кельвина.

8. Расстояние от наблюдателя, выраженное в километрах, находящегося на высоте h метров над землей, до видимой им линии горизонта вычисляется по формул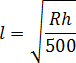е: , где

R = 6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 6,4 километра. К пляжу ведет лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек надо подняться человеку, чтобы он увидел горизонт на расстоянии не менее 11,2 километра?

9. В боковой стенке цилиндрического бака вблизи дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем меняется по закону:

H(t) = at² + bt + H₀, где H₀ = 2 м — начальный уровень воды, a = 1/50 м/мин² и b = −2/5 м/мин — постоянные. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.

10. Для определения эффективной температуры звезд используют закон Стефана — Больцмана, согласно которому мощность излучения нагретого тела прямо пропорциональна площади его поверхности и четвертой степени температуры: , где σ = 5,7 · 10⁻⁸ — постоянная, площадь измеряется в квадратных метрах, температура — в градусах Кельвина, а мощность — в ваттах. Известно, что некоторая звезда имеет площадь S = (1/81) · 10¹² м², а излучаемая ею мощность P не менее 46,17 · 10²¹ Вт. Определите наименьшую возможную температуру этой звезды. Ответ дайте в градусах Кельвина.

11. Некоторая компания продает свою продукцию по цене p = 400 руб. за единицу, переменные затраты на производство одной единицы продукции составляют v = 200 руб., постоянные расходы предприятия f = 200 000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле: π (q) = q(p − v) − f. Определите наименьший месячный объем производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не менее 300 000 руб.

12. При температуре 0 °С рельс имеет длину l₀ = 15 метров. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону:

l(t°) = l₀ · (1 + a · t°), где a = 1,2 · 10⁻⁵ (°C)⁻¹ — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 6,3 мм? Ответ выразите в градусах Цельсия.

Самостоятельная работа

2 вариант

1. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой: . При каком наименьшем значении температуры нагревателя T₁ КПД этого двигателя будет не менее 60%, если температура холодильника T₂ = 400?

2. В ходе распада радиоактивного изотопа его масса уменьшается по закону: 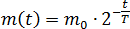, где m₀ (мг) — начальная масса изотопа, t (мин) — время, прошедшее от начального момента, T (мин) — период полураспада. В лаборатории получили вещество, содержащее в начальный момент времени m₀ = 60 мг изотопа золота, период полураспада которого T = 15 мин. В течение скольких минут масса изотопа будет не менее 15 мг?

3. Для определения эффективной температуры звезд используют закон Стефана — Больцмана, согласно которому мощность излучения нагретого тела прямо пропорциональна площади его поверхности и четвертой степени температуры: , где σ = 5,7 · 10⁻⁸ — постоянная, площадь измеряется в квадратных метрах, температура — в градусах Кельвина, а мощность — в ваттах. Известно, что некоторая звезда имеет площадь S = (1/256) · 10¹³ м², а излучаемая ею мощность P не менее 9,12 · 10²² Вт. Определите наименьшую возможную температуру этой звезды. Ответ дайте в градусах Кельвина.

4. При температуре 0 °С рельс имеет длину l₀ = 10 метров. При прокладке путей между рельсами оставили зазор в 3 мм. При возрастании температуры будет происходить тепловое расширение рельса, и его длина будет меняться по закону: l(t) = l₀ · (1 + a · t), где a = 1,2 · 10⁻⁵ (°C)⁻¹ — коэффициент теплового расширения, t — температура (в градусах Цельсия). При какой минимальной температуре зазор между рельсами исчезнет? Ответ выразите в градусах Цельсия.

5. В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону: , где t — время в секундах, прошедшее с момента открытия крана, H₀ = 5 м — начальная высота столба воды, k = 1/800 — отношение площадей поперечных сечений крана и бака, а g = 10 м/с² — ускорение свободного падения. К какому моменту времени в баке останется не более чем четверть первоначального объема воды? Ответ выразите в секундах.

6. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур дается выражением: T(t) = T₀ + bt + at², где T₀ = 1400 К, a = −50 К/мин, b = 400 К/мин². Известно, что при температуре нагревателя свыше 1750 К прибор может испортиться, поэтому его нужно отключать. Определите (в минутах), через какое наибольшее время после начала работы нужно отключать прибор.

7. Модель камнеметательной машины выстреливает камни под определенным углом к горизонту с фиксированной начальной скоростью. Траектория полета камня в системе координат, связанной с машиной, описывается формулой: y = ax² + bx, где a = −1/100 м⁻¹, b = 1 — постоянные параметры, x — расстояние от машины до камня, считаемое по горизонтали, y — высота камня над землей. На каком наименьшем расстоянии от крепостной стены высотой 8 метров надо расположить машину, чтобы камни пролетали над ней на высоте не менее 1 метра? Ответ выразите в метрах.

8. В розетку электросети подключены приборы, общее сопротивление которых составляет R = 50 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите (в Омах) наименьшее возможное сопротивление этого электрообогревателя, если для нормального функционирования электросети общее сопротивление в ней должно быть не менее 25 Ом. При этом известно, что при параллельном соединении двух проводников с сопротивлениями R_x и R_y их общее сопротивление дается формулой: .

9. После дождя уровень воды в колодце может повыситься. Мальчик определяет его, измеряя время падения t небольших камушков в колодец и рассчитывая по формуле: h = −5t², где t измеряется в секундах, а h — в метрах. До дождя время падения камушков составляло 0,6 секунды. На какую минимальную высоту должен подняться уровень воды после дождя, чтобы измеряемое время изменилось больше чем на 0,1 секунды? Ответ выразите в метрах.

10. По закону Ома для полной цепи сила тока, измеряемая в амперах, равна:

где ε — ЭДС источника (в вольтах), r = 2 Ом — его внутреннее сопротивление, R — сопротивление цепи (в Омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания I_кз = ε/r? Ответ выразите в Омах.

11. Операционная прибыль предприятия в краткосрочном периоде вычисляется по формуле:

π (q) = q(p − v) − f. Компания продает свою продукцию по цене p = 600 руб. за штуку, переменные затраты на производство одной единицы продукции составляют v = 300 руб. за штуку, постоянные расходы предприятия f = 700 000 руб. в месяц. Определите наименьший месячный объем производства q (шт.), при котором прибыль предприятия будет не менее 500 000 руб. в месяц.

12. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением a км/ч², вычисляется по формуле: .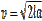

Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,4 километра, приобрести скорость не менее 160 км/ч. Ответ выразите в км/ч².