Муниципальное казенное общеобразовательное учреждение «Гирьянская средняя
общеобразовательная школа» Беловского района Курской области
Клейменова Валентина Ивановна учитель математики высшей квалификационной категории
Функциональный метод решения уравнений и неравенств
В соответствии с обязательным минимумом содержания среднего (полного) общего образования, утвержденным Министерством образования РФ (пр. №56 от 30.06.99), все учащиеся должны знать три основных метода решения уравнений:
разложение на множители,
замена переменных,
использование свойств функций.
К сожалению, в общеобразовательной школе очень мало времени уделяется решению уравнений и неравенств функциональным методом.
___________________________________________----
Рассмотрим нестандартные методы решения уравнений и неравенств, основанные на свойствах функций: области определения, области значения, монотонности, четности, периодичности .
Использование области определения функции Областью определения функции f(x) называется множество значений, которые принимает независимая переменная (аргумент). Областью определения уравнения f(x)=g(x) (ОДЗ) называются все значения переменной х при которых определена как функция f(x), так и функция g(x).
________________________________________________________
Пример1. Решите уравнение: 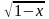 +
+ 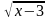 =5
=5
Решение.
 ОДЗ: 1-x
ОДЗ: 1-x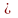 0, x
0, x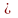 1, решений нет.
1, решений нет.
x-3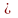 0 x
0 x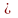 3
3
Ответ: Ø
_______________________________________________________________________________-
Пример2. Решите уравнение: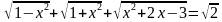
Решение: Первый радикал определен при 1-x2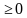 -1
-1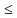 x
x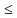 1.
1.
Второй определен для любых значений x .
Третий определен, если 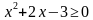 x -3 или x 1
x -3 или x 1
Т.О. 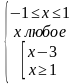
Проверка показывает, что x=1, корень.
Ответ: 1
_______________________________________________________________----
Пример3 Решить неравенство:
![]()
![]()
ОДЗ:
: 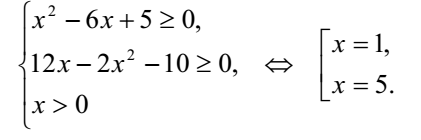
Подставляя полученные значения в данное неравенство, получим: при x 1 исходное неравенство примет вид 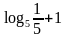 =0 , значит 1- не корень.
=0 , значит 1- не корень.
При x = 5 получим 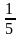 , значит 5 – корень.
, значит 5 – корень.
Ответ: 5
__________________________________________________________________----
Реши самостоятельно:
1).Реши неравенство ![]()
Ответ:.1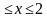
2).Реши уравнение: 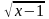 +
+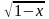 = x
= x - 1 Ответ:1
- 1 Ответ:1
_______________________-----____________-
Использование свойства монотонности :
Теорема 1. Если одна из функций y=f(x), y=g(x) убывает, а другая возрастает на
промежутке Х, то на этом промежутке уравнение f(x)=g(x) имеет не более одного корня.
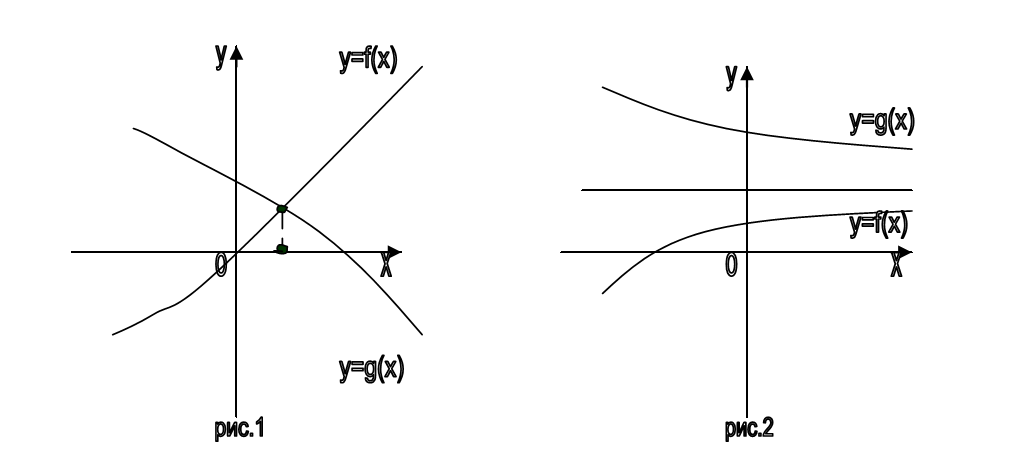
Теорема 2. Если f(x) возрастает на промежутке Х (или f(x) убывает на промежутке Х), то уравнение f(x)=C, где C=const, на промежутке Х имеет не более одного корня
то уравнение f(x)=C, где C=const, на промежутке Х имеет не более одного корня.
______________________________-
Пример 4. Решите уравнение:
Решение.
ОДЗ:
Функция х 2 +
убывает на промежутке (-
;-0], а
- постоянная функция.
Подбором находим, что x =- - 4. В силу теоремы 2, найденный корень единственный.
Ответ: - 4.
Пример5. Решите уравнение: 2 arcsin 2x = 3 arccos x
Данное уравнение есть уравнение вида f(x) = g(x), где f(x) = 2 arcsin2x и g(x)=3 arccos x f(x) возрастает на D (f), g(x) убывает на D (g). Следовательно, уравнение имеет не более одного
корня. Подбором находим, что x =- 0,5. Ответ: 0,5
Пример 6 Решите неравенства: 2x5+x3+5x-80
Решение: Рассмотрим функции f(x)= 2x5+x3+5x-80 и g(x)= Эти функции определены и дифференцируемы на R. Исследуем f(x) на монотонность: f(x) 10x 4 3x 2 5 0 , как сумма неотрицательных слагаемых и положительного слагаемого. Поэтому функция f(x) строго возрастает на R. Функция g(x) определена на R и дифференцируема на множестве , причем
,
Значит, функция g(x) убывает на R. Поскольку функция f(x) строго возрастает, а функция g(x) убывает на R, то уравнение f(x) g(x) имеет не больше одного корня. Подбором находим, что
x 2 является корнем этого уравнения,
Ответ: 2
Реши самостоятельно:
1) Решите уравнение
Ответ: 1.
2) Решите неравенство
Ответ: .
3) Решите неравенство .
Ответ:
Использование ограниченности функций.
Для использования ограниченности функции необходимо уметь находить множество значений функции и знать оценки области значений стандартных функций (например, 1 sin x 1 , .
Теорема 1: Если
Пример 7. Решите уравнение .
Решение. Перепишем уравнение в виде: .
Поскольку и , следовательно, данное уравнение равносильно системе
Ответ: -1.
Пример 8. Решите уравнение
Решение. Заметим, что и
Следовательно,неравенство может быть выполнено только при условии, что , а это достигается при
, что невозможно.
Ответ: нет решений.
Следствие теоремы 1: Если для любого справедливы неравенства
и
где А – некоторое число, то на множестве М уравнение
и неравенство
решений не имеют.
Роль числа А часто играет нуль, в этом случае говорят о сохранении знака функций f(x) и g(x) на множестве М.
Пример 9. Решите уравнение .
Решение. 1. Заметим, что . Воспользуемся этим неравенством для левой части уравнения:
.
2. В правой части уравнения получим: . Тогда .
Ответ: нет корней..
Пример 10. Найти все значения параметра а, при каждом из которых уравнение
имеет решения. Найдите эти решения
Решение. Перепишем уравнение в виде
При всех значениях х выражение
а выражение Следовательно получаем систему
Ответ: x= , a =
Реши самостоятельно: Найти все значения параметра а при которых уравнение
имеет решение.
Ответ:5
Метод оценок. Признаком применения этого метода является наличие в уравнении функций разной природы.
.
.

 Получите свидетельство
Получите свидетельство Вход
Вход













 Функциональный метод решения уравнений и неравенств (201.14 KB)
Функциональный метод решения уравнений и неравенств (201.14 KB)
 0
0 163
163 7
7 Нравится
0
Нравится
0


