Авторская программа элективного курса по математике
для учащихся 11 класса
«Применение метода координат при решение задач ЕГЭ уровня С2»
учителя математики 1 квалификационной категории МОУ Вохомская средняя общеобразовательная школа Вохомского района Костромской области
Адеевой Галины Витальевны.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Элективный курс«Применение метода координат при решение задач ЕГЭ уровня С2» разработан в рамках реализации концепции профильного обучения на старшей ступени общего образования и соответствует Государственному стандарту среднего образования по математике. При разработке данной программы учитывалось то, что элективный курс как компонент образования должен быть направлен на удовлетворение познавательных потребностей и интересов старшеклассников, на формирование у них новых видов познавательной и практической деятельности, которые не характерны для традиционных учебных курсов.
Программа элективного курса по теме ориентирована на коррекцию уровня подготовки, дополнение и углубление базового и предметного образования, компенсацию недостатков обучения по профильным предметам. Математика является обязательным предметом для сдачи ЕГЭ и о немалую часть материала единого государственного экзамена составляют задачи по геометрии. Результаты ЕГЭ показывают пробелы изучения геометрии в школе. Самыми трудными заданиями по математике являются геометрические задачи.
Особого внимания требуют вопросы, связанные с вычислением расстояний и углов в пространстве применительно к конкретной фигуре. Они остаются трудными для большинства учащихся, причем, даже в тех достаточно типичных ситуациях, которые используются в задачах повышенного уровня. Так, если в задачах высокого уровня сложности рассматривается угол между двумя плоскостями, которые зачастую являются плоскостями боковых граней или плоскостями проведенных сечений, то в задачах повышенного уровня это угол между плоскостью основания и плоскостью боковой грани пирамиды или плоскостью типичного сечения призмы. Задачи, связанные с такими ситуациями, из года в год присутствуют в вариантах ЕГЭ (как и в вариантах многих вступительных экзаменов в вузы), тем не менее, процент их верного решения невысок. Это объясняется двумя причинами. Первая причина связана с тем, что углы между плоскостями (а также другие вопросы, связанные с углами и расстояниями в пространстве) в учебниках часто рассматриваются и проходят первичное закрепление до изучения многогранников и тел вращения. Вторая причина связана с задачами, в которых рассматриваются углы между прямой и плоскостью или между плоскостями, где необходимо применять планиметрический материал, нередко усвоенный непрочно. В данном случае речь идет о решении прямоугольных (реже – косоугольных) треугольников.
В школьном курсе стереометрии упор делается на дополнительные построения, которые позволяют выделить искомый угол, а затем рассчитать его величину.
Здесь уместно вспомнить задачи на построение сечений многогранников, которые рассматриваются в 10 классе и у многих вызывают трудности. Существование формального алгоритма для таких построений совершенно не облегчает задачу, поскольку каждый случай достаточно уникален, а любая систематизация лишь усложняют процесс.
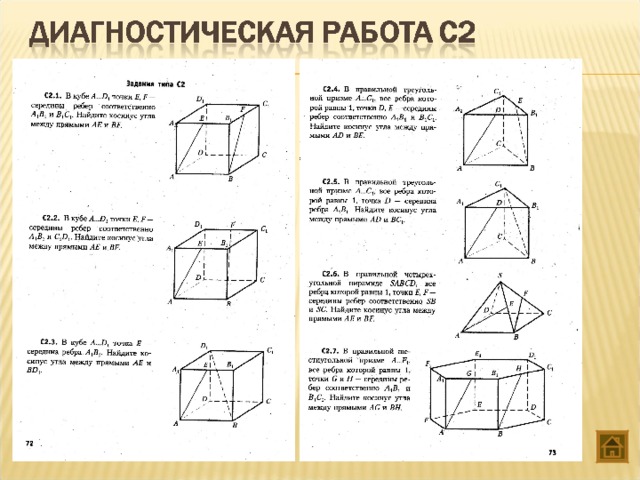
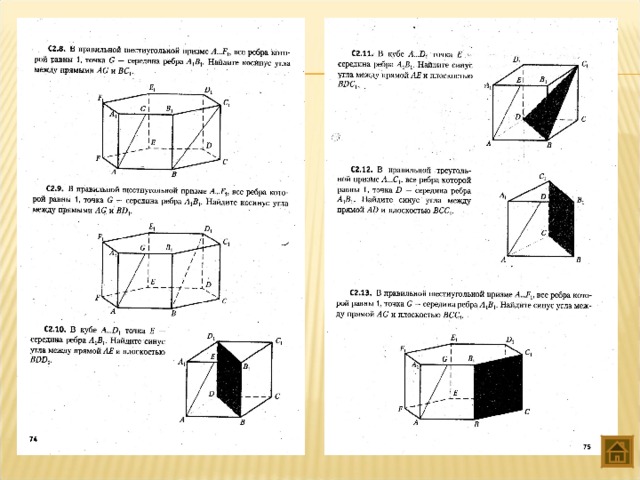
Именно поэтому задача C2 оценивается в два балла. Первый балл дается за правильные построения, а второй — за правильные вычисления и собственно ответ.
Преимущества традиционного решения:
Высокая наглядность дополнительных построений, которые подробно изучаются на уроках геометрии в 10-11 классах;
При правильном подходе значительно сокращается объем вычислений.
Недостатки:
Необходимо знать большое количество формул из стереометрии и планиметрии;
Дополнительные построения каждый раз приходится придумывать «с нуля». И это может оказаться серьезной проблемой даже для хорошо подготовленных учеников.
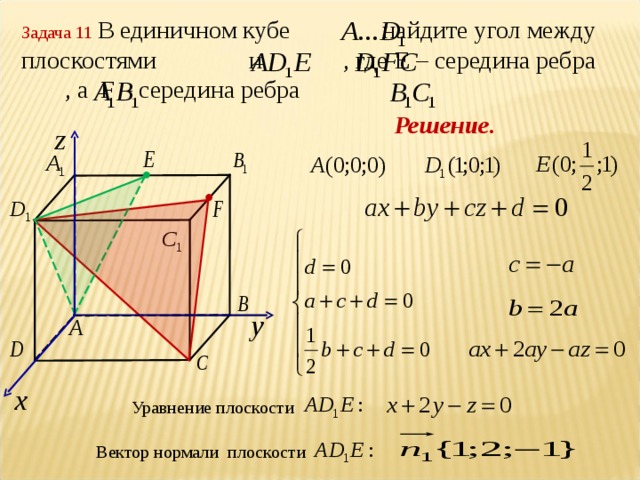
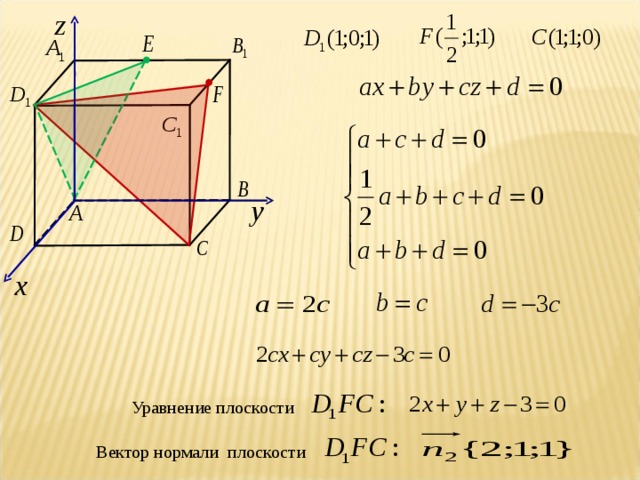
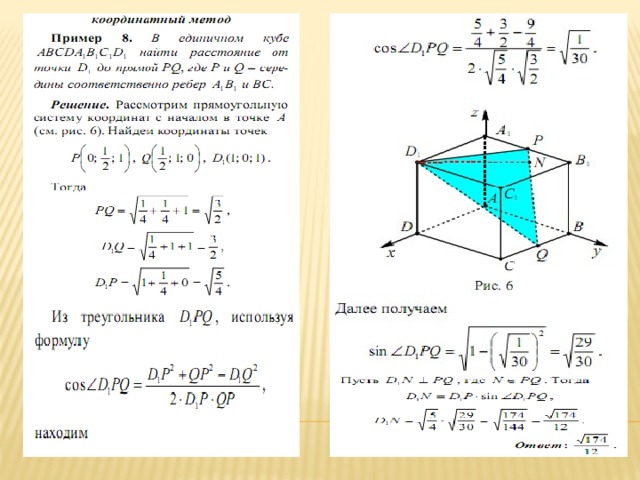
В методе координат главная нагрузка приходится на алгебраические выкладки, однако их целесообразность базируется на наглядном осмыслении задачи. Что же требуется , чтобы освоить метод координат? 1)знание определенных формул; 2) умение вычислять координаты вершин многогранников и точек, расположенных на их ребрах и гранях; 3)умение составлять уравнение плоскости, проходящей через три заданные точки.
Цели курса:
- углубить теоретическое и практическое содержание курса стереометрии;
- развивать пространственные представления и логическое мышление;
- развивать умение применять знания на практике, приводить аргументированное решение, анализировать условие задачи и выбирать наиболее рациональный способ решения.
- Формирование системы знаний по теме «Метод координат»
Задачи курса:
- расширить и углубить представления учащихся о приемах и методах решения стереометрических задач;
- создать условия для выдвижения различных гипотез при поиске решения задачи и доказательства истинности или ложности этих гипотез;
- развивать интерес и положительную мотивацию изучения геометрии, создавать условия для подготовки учащихся к успешной сдаче ЕГЭ по математике.
Основной тип занятий - практикум. Для наиболее успешного усвоения материала планируются различные формы работы с учащимися: лекционные и практические занятия, с использованием презентаций, групповые, индивидуальные формы работы.
Весь теретический и практический материал крса представлен в презентациях,которые прилагаются к данной рабочей программе.
В результате изучения курса учащиеся должны уметь:
- выполнять чертежи по тексту задачи; находить углы и расстояния в пространстве
- точно и грамотно формулировать теоретические положения и излагать собственные рассуждения в ходе решения задач;
- уметь анализировать задачу и выбирать наиболее рациональный способ ее решения.
УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН
| № п/п | Наименование тем курса | Всего часов |
| 1 | Метод координат. Повторение основных понятий. | 1 |
| 2 | Введение системы координат | 1 |
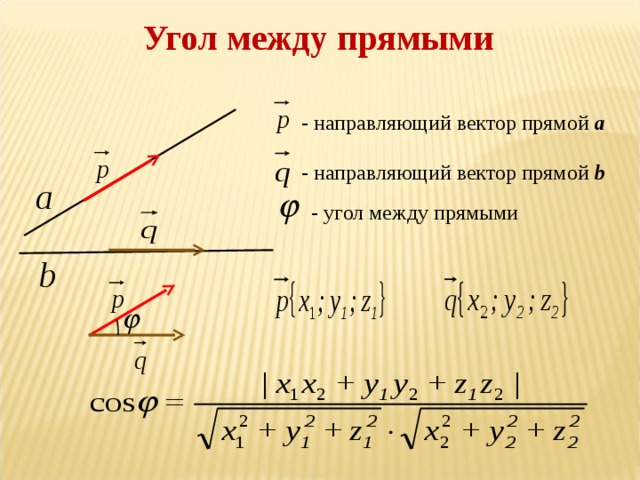
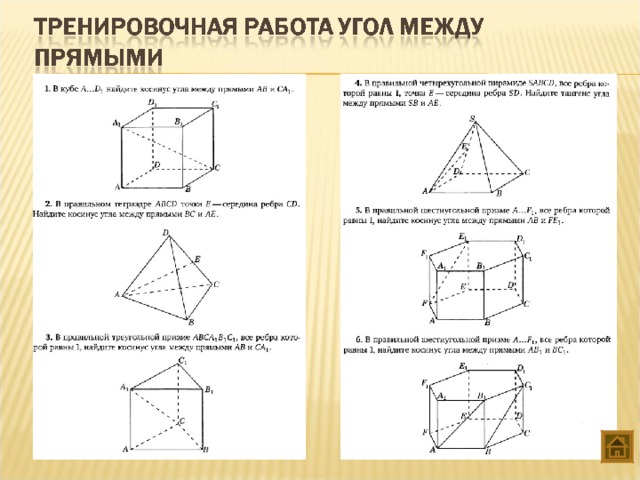
| 3 | Угол между прямыми | 2 |
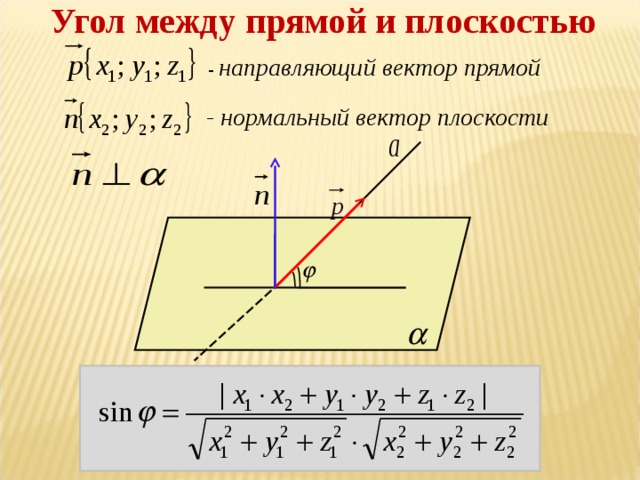
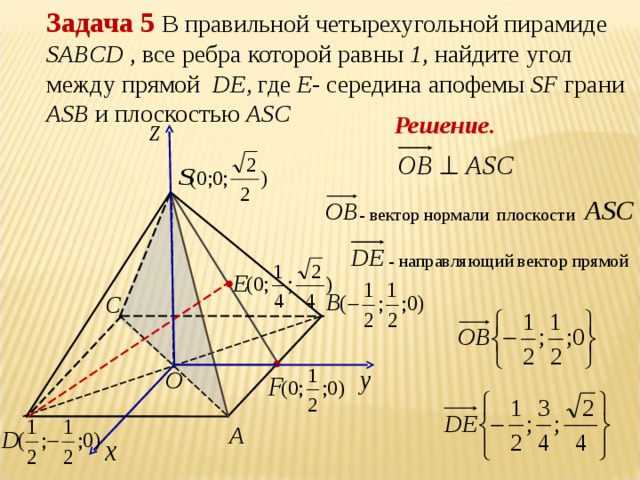
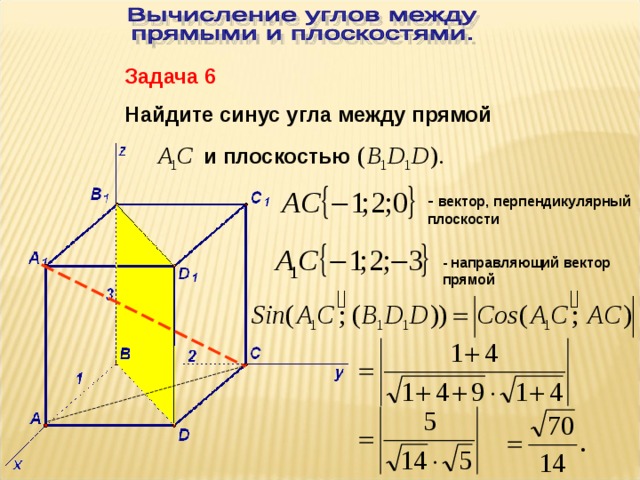
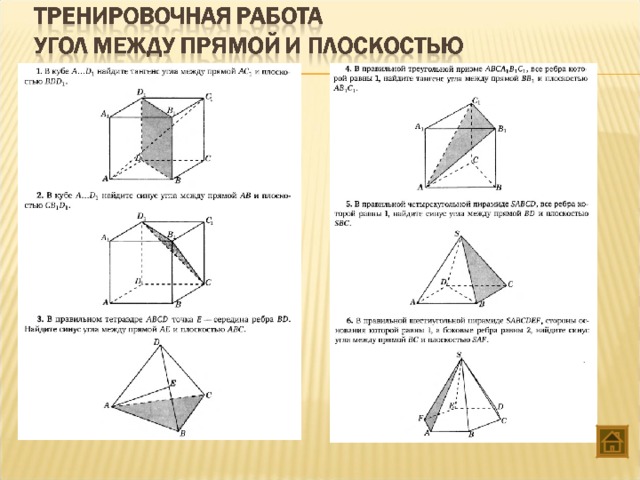
| 4 | Угол между прямой и плоскостью | 2 |
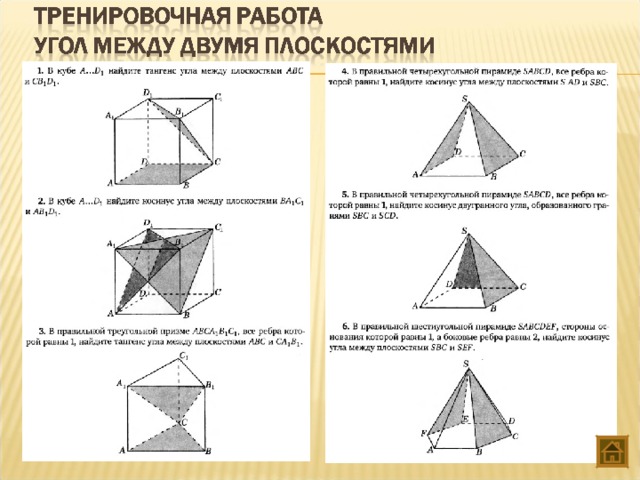
| 5 | Угол между плоскостями | 2 |
| 6 | Расстояние между точками |
2 |
| 7 | Расстояние от точки до плоскости | 2 |
| 8 | Расстояние от точки до прямой | 2 |
| 9 | Расстояние между скрещивающимися прямыми | 2 |
|
| Всего | 16 |
СОДЕРЖАНИЕ ПРОГРАММЫ КУРСА
Тема 1. Метод координат. Повторение основных понятий.
Понятие вектора.Координаты вектора.Угол между векторами.Понятие нормали.Уравнение плоскости.
Тема 2. Введение системы координат
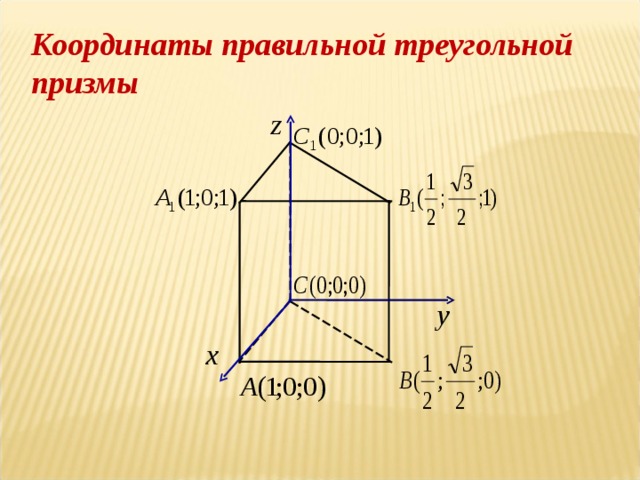
Оптимальный вариант введения системы координат.Призма,пирамида.
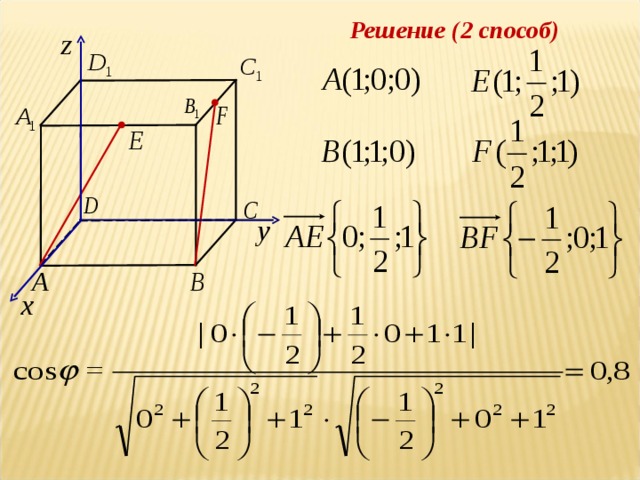
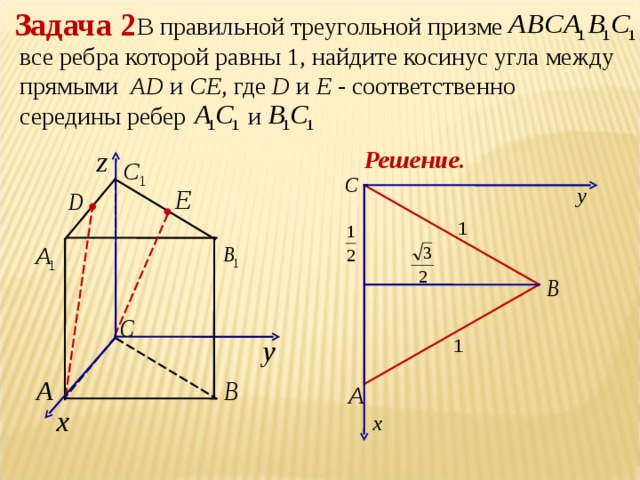
Тема 3. Угол между прямыми
Нахождение угла между прямыми методом координат.
Тема 4. Угол между прямой и плоскостью
Нахождение угла между прямой и плоскостью методом координат
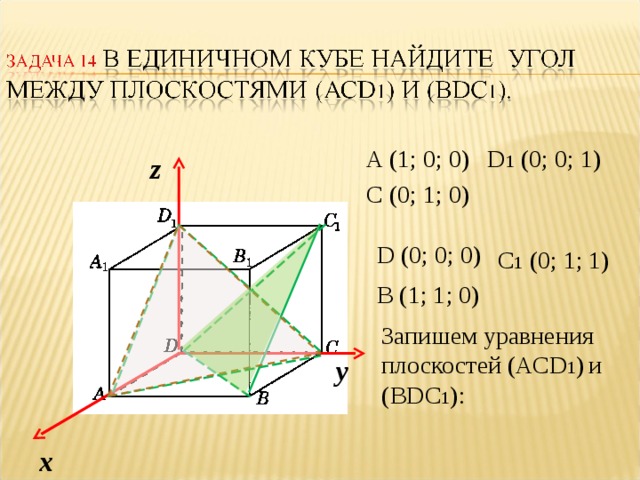
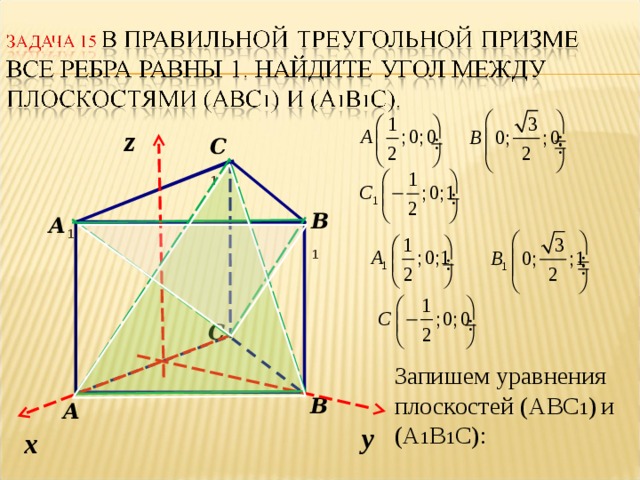
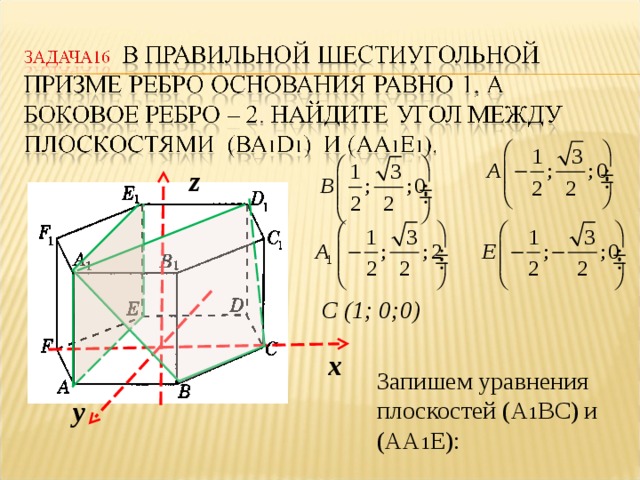
Тема 5. Угол между плоскостями
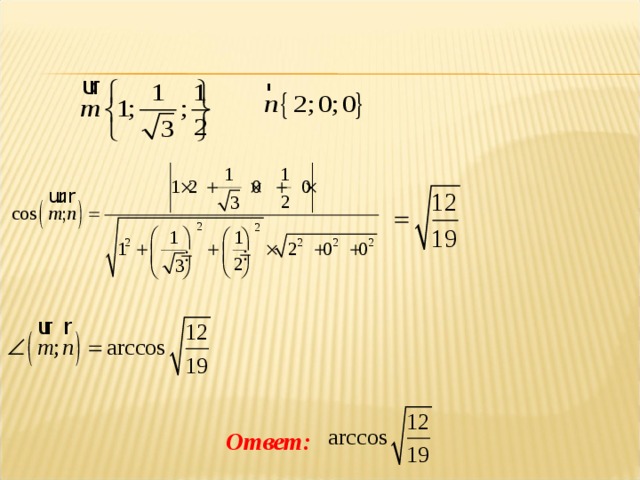
Нахождение угла между плоскостями методом координат
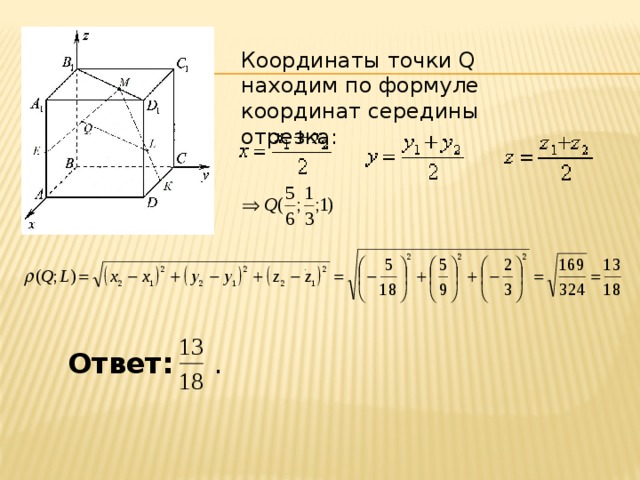
Тема 6.Расстояние между точками
Нахождение расстояний между точками методом координат
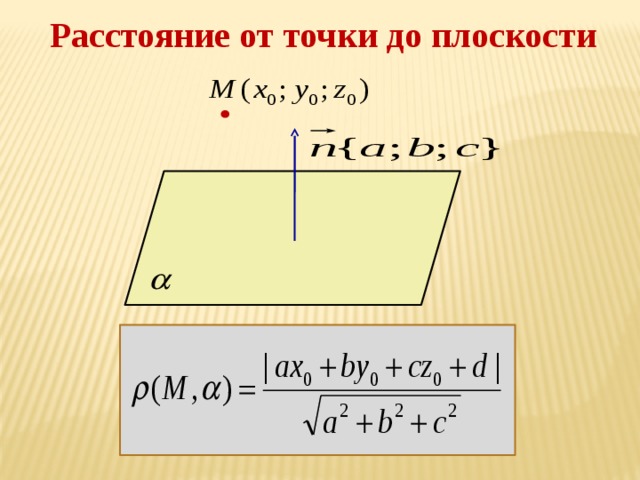
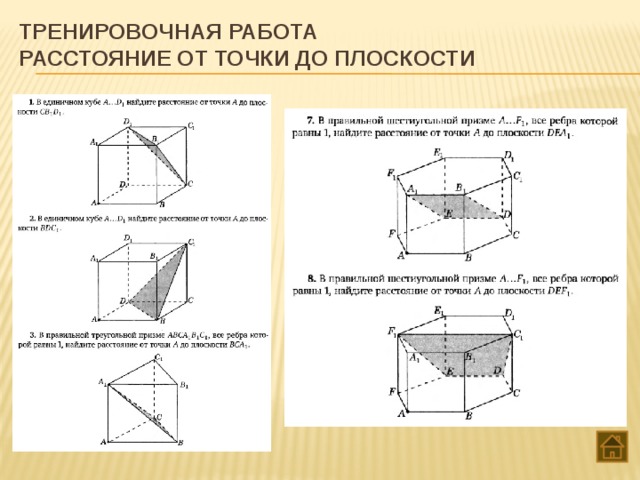
Тема 7. Расстояние от точки до плоскости
Нахождение расстояний от точки до плоскости методом координат
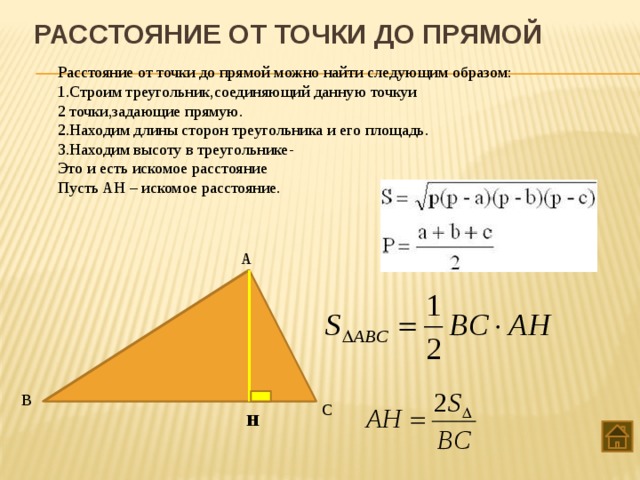
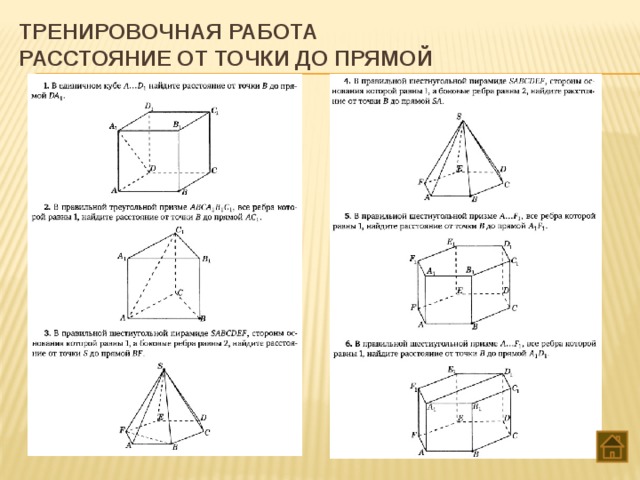
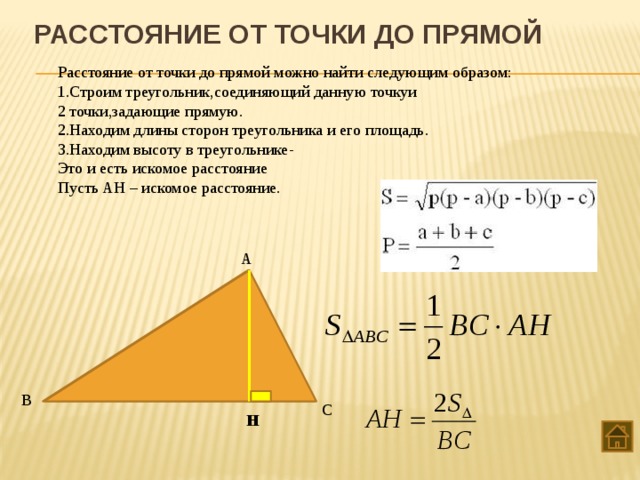
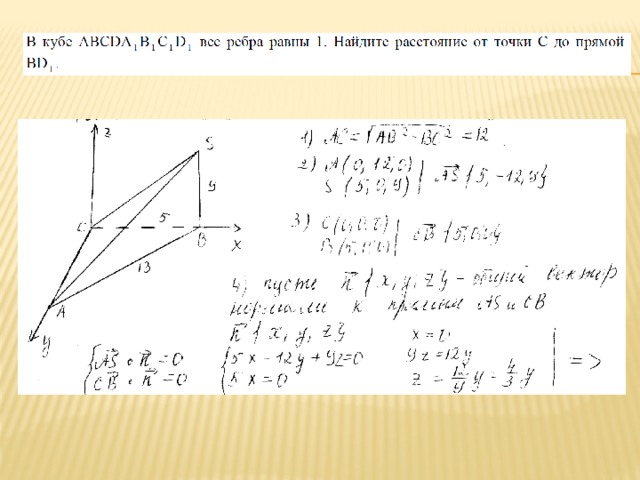
Тема 8. Расстояние от точки до прямой
Нахождение расстояний от точки до прямой методом координат
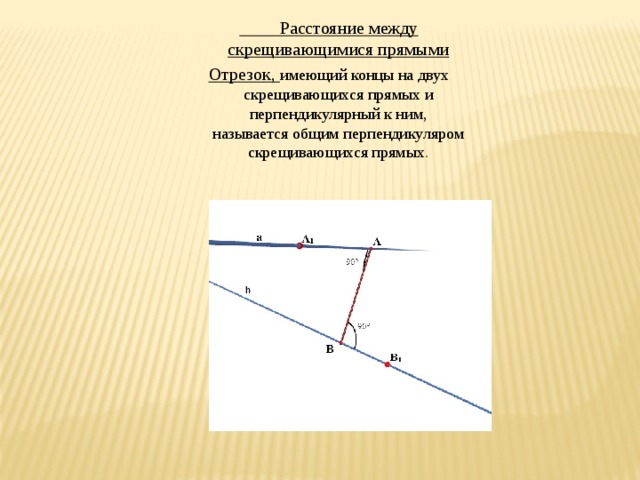
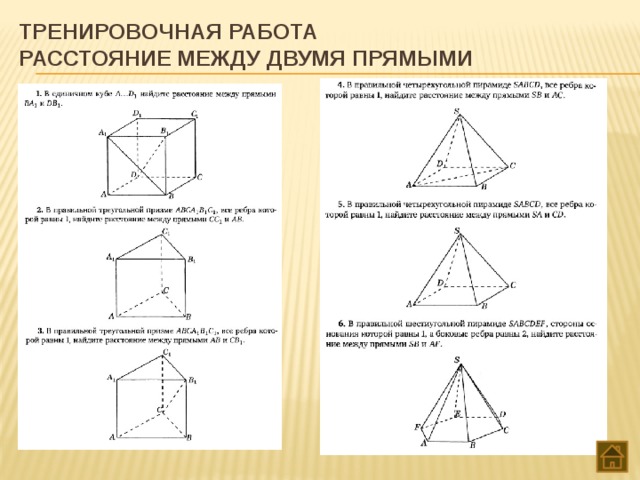
Тема 9. Расстояние между скрещивающимися прямыми
Нахождение расстояний между скрещивающимися прямыми методом координат
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения. МАТЕМАТИКА ЕГЭ 2013 (типовые задания С2)
ЕГЭ 2010.Математика. Задача С2 . Смирнов В.А./Под ред. А.Л.Семенова и И.В.Ященко. М.:МЦНМО, 2010
ЕГЭ 2010. Математика. Универсальные материалы для подготовки учащихся. Авт.-сост. Высоцкий И.Р., Гущин Д.Д. и др. /ФИПИ- М.; Интеллект-Центр, 2010.
Смирнова И.М. ,Смирнов В.А.Расстояния и углы в пространстве(Москва,2009 г.)

 Получите свидетельство
Получите свидетельство Вход
Вход




















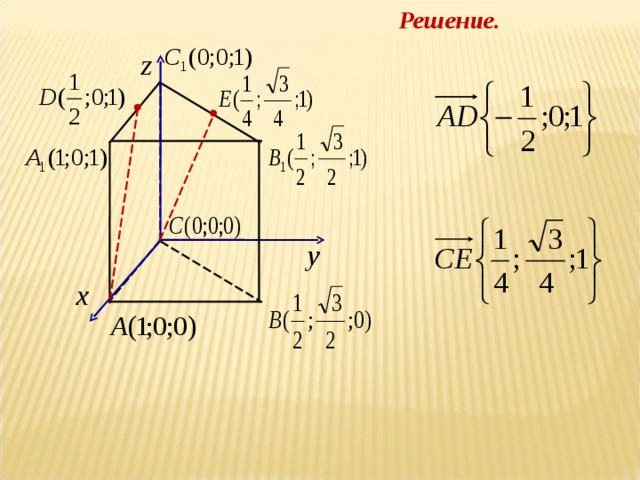

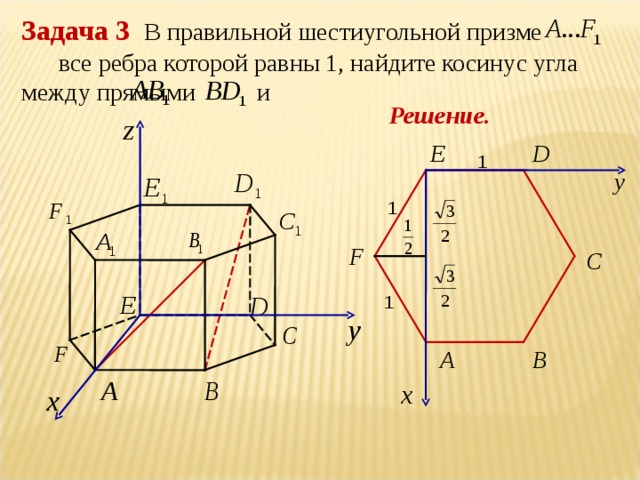
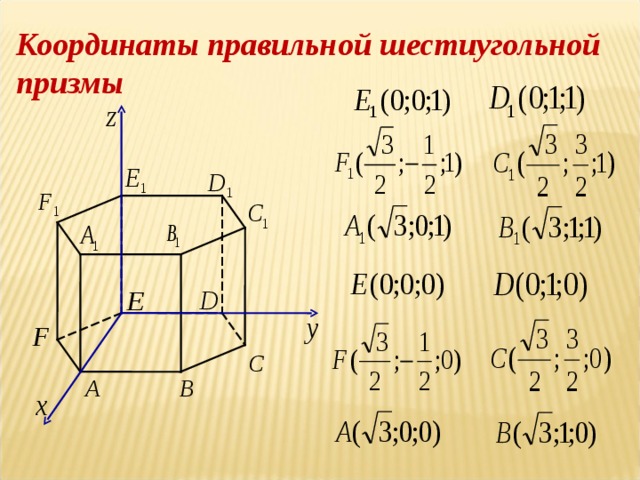
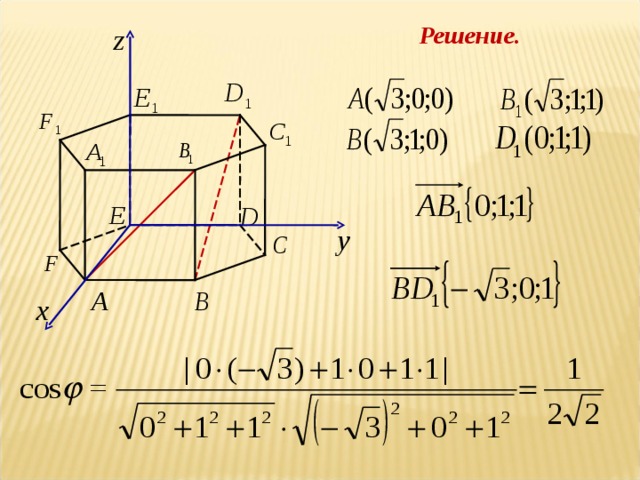
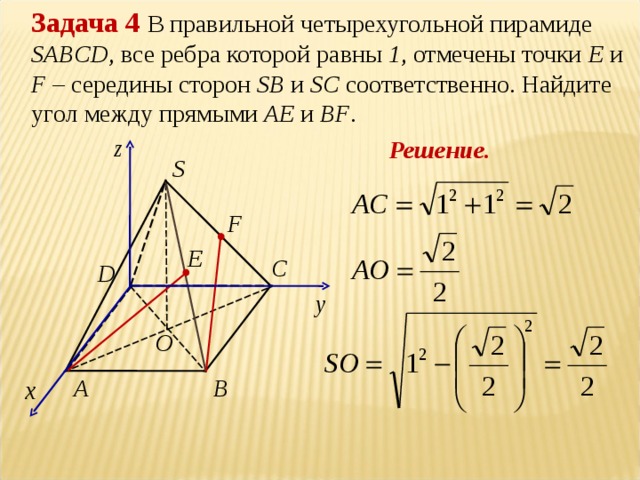
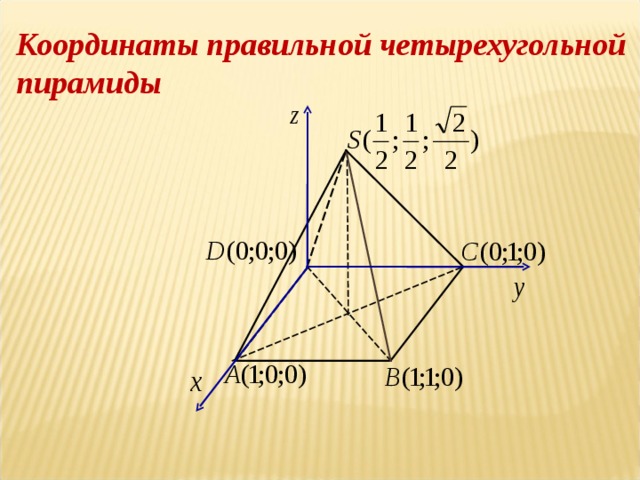
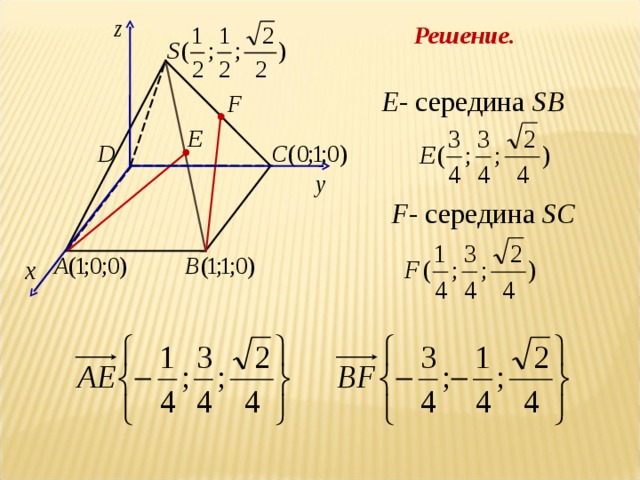
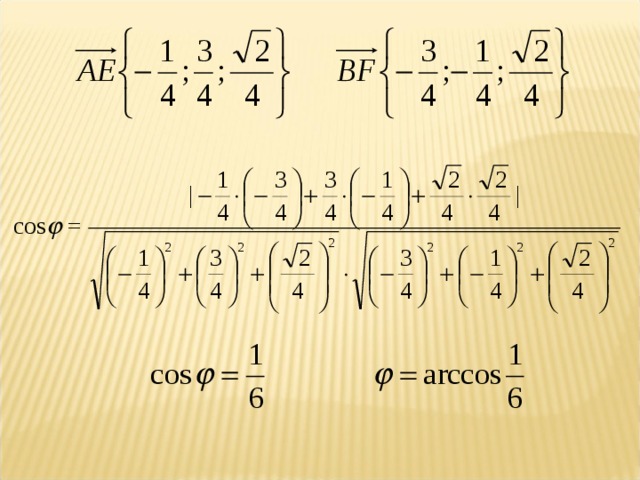

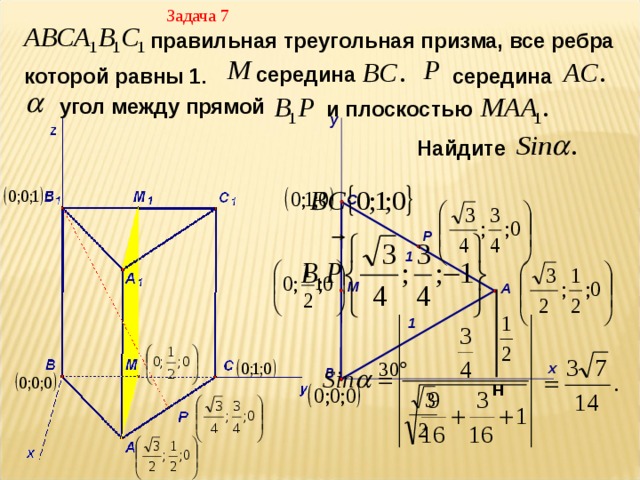
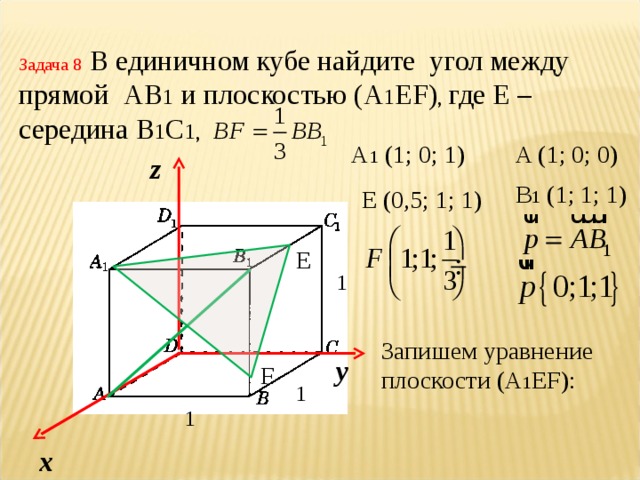


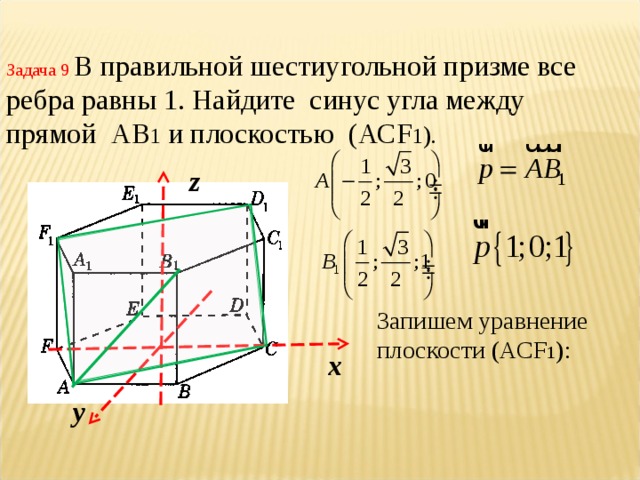


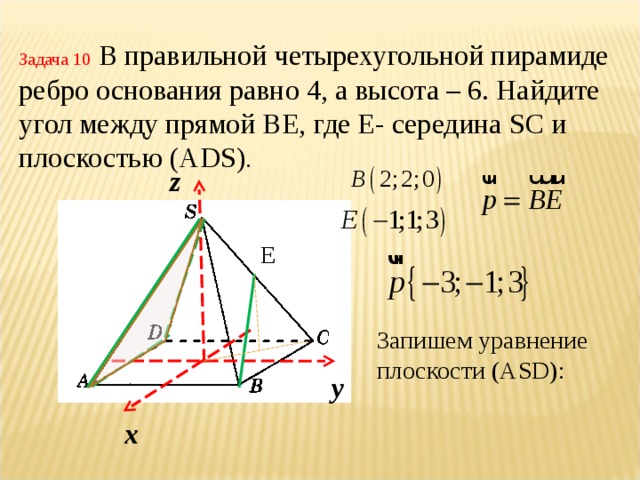



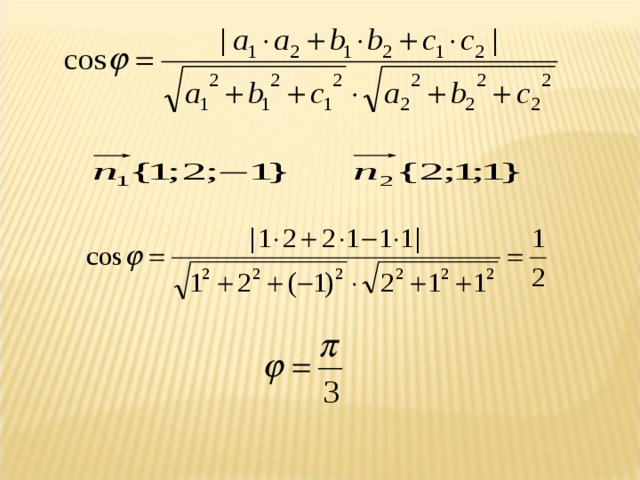





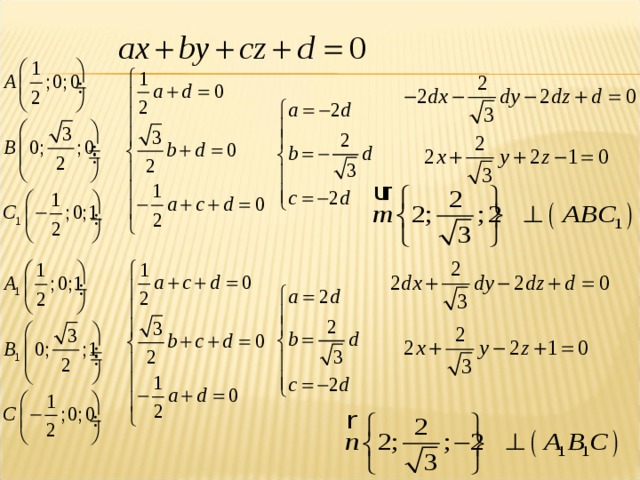

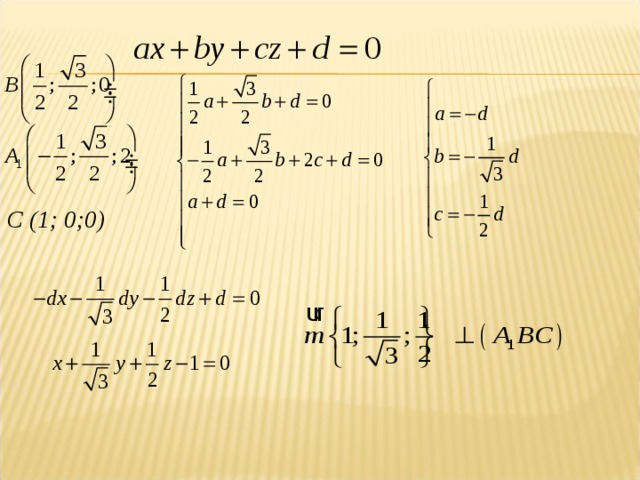
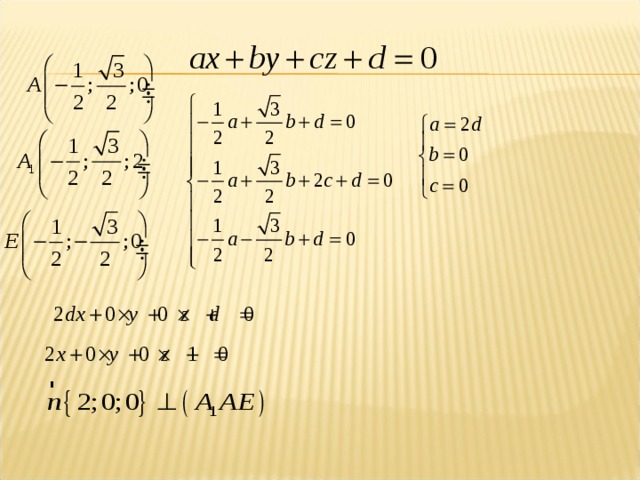


























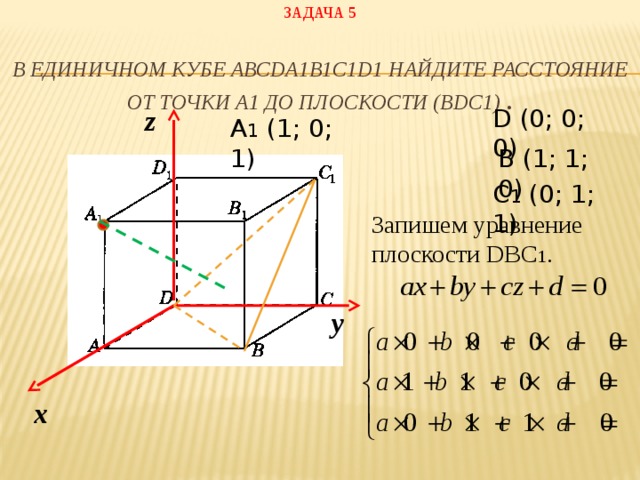

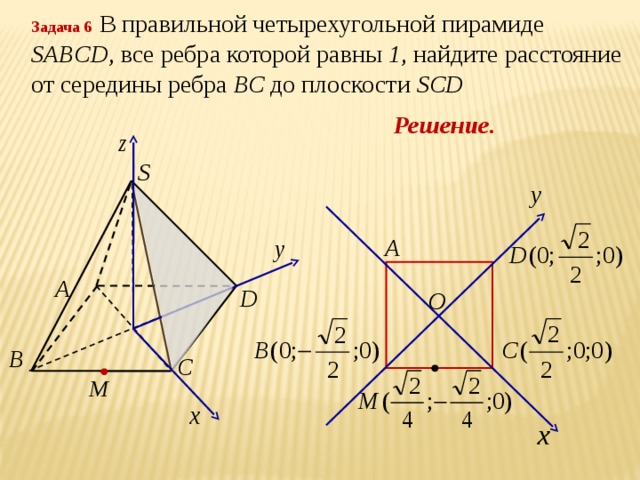
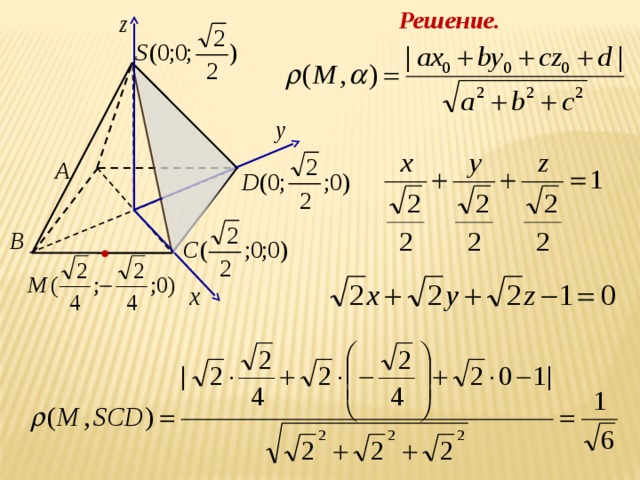
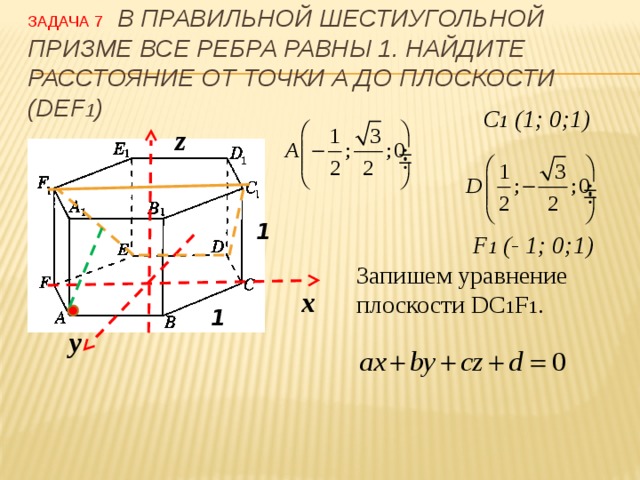
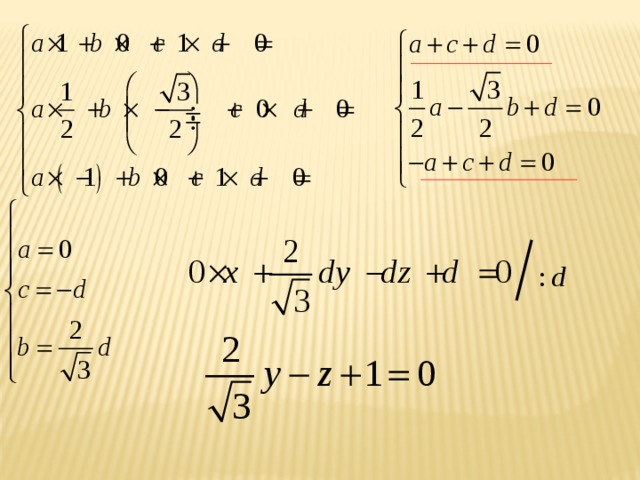




















 Элективный курс по теме " Метод координат" (8.43 MB)
Элективный курс по теме " Метод координат" (8.43 MB)
 0
0 1411
1411 80
80 Нравится
0
Нравится
0


