Декартова система координат в пространстве. Построение точек и вычисление расстояния между ними

Группа

Дата

Дисциплина

Математика

Тема занятия

Декартова система координат в пространстве. Построение точек и вычисление расстояния между ними

Вид занятия

Урок усвоения новых знаний (теоретическое)

образовательные:

Цель занятия

Рассмотреть понятие системы координат и координат точки в пространстве, показать, максимально используя наглядность, что координаты в пространстве вводятся так же легко и естественно, как и координаты на плоскости

развивающие:

- развивать познавательный интерес учащихся, учить их видеть связь между математикой и окружающей жизнью; развивать грамотную математическую речь; развивать логическое мышление, умение самостоятельно работать, навыки взаимоконтроля и самоконтроля, умение говорить и слушать;

воспитательные:

- воспитывать волю и настойчивость для достижения конечных результатов

- воспитание уважительного отношения к одноклассникам

ОК 2 Организовывать собственную деятельность, определять методы решения профессиональных задач, оценивать их эффективность и качество.

ОК 3 Оценивать риски и принимать решения в нестандартных ситуациях

ОК 4 Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.

ОК 5 Использовать информационно-коммуникационные технологии для совершенствования профессиональной деятельности.

ОК 6 Работать в коллективе и команде, взаимодействовать

Показатели оценки

результата

Должны знать

• знать определение и свойства

Должны уметь

• уметь применять при решении примеров полученные ранее знания

Межпредметные

связи

Обеспечивающие

дисциплины

Физика, русский язык

Обеспечиваемые

дисциплины

Физика, химия, черчение, русский язык

Средства

Доска, мел, учебник

обучения

Основная

А.Н. Колмогоров «Алгебра и начала математического анализа 10-11 кл.»

литература

М.И. Башмаков «Математика (СПО)»

№

этапа

Этапы занятия, учебные вопросы,

формы и методы обучения

Временная

регламентация

этапа

1

Организационный этап:

5

ДИДАКТИЧЕСКАЯ ЗАДАЧА – подготовить обучающихся к работе на уроке.

СОДЕРЖАНИЕ – взаимные приветствия, фиксация отсутствующих, проверка внешнего состояния аудитории и готовности обучающихся к занятию, организация внимания.

- Сообщение правил заполнения листа самоанализа:

Критерий оценивания:

2.

Этап проверки домашнего задания

15

ДИДАКТИЧЕСКАЯ ЗАДАЧА – установить правильность и осознанность выполнения домашнего задания всеми обучающимися, установить в ходе проверки обнаруженные пробелы в знаниях, совершенствую при этом знания, умения, навыки.

Содержание: фронтальный опрос, карточки с заданиями

1. Как можно двигаться по прямой?

2. Сколькими координатами может быть задана точка на прямой?

3. Назовите координаты точек на координатной оси?

4. В каком направлении можно двигаться на плоскости?

5. Чем определяются точки на координатной плоскости?

6. Что такое координата?

7. Как задать координатную плоскость?

8. Как называется ось 0Х, 0У?

9. Назовите координаты точек (по графику)

3

Этап подготовки обучающихся к активному и сознательному усвоению материала

10

ДИДАКТИЧЕСКАЯ ЗАДАЧА – организовать и направить на достижение цели познавательную деятельность обучающихся, постановка целей учебной деятельности.

«За всю историю человечества пока не найдено лучшего способа развития интеллектуальных и творческих способностей человека , чем при помощи математики» Владимир Тихомиров, профессор МГУ.

1. Сообщение темы, цели и задач материала

2. Какую тему созвучную с темой нашего урока Вы изучали в школе? Какое ключевое слово определяют эти две темы? (Координаты). 

3. Координаты на плоскости и в пространстве можно вводить бесконечным числом различных способов.

4. Решая геометрическую, физическую, химическую задачу можно использовать различные координатные системы: прямоугольную, полярную, цилиндрическую, сферическую. (Показ моделей кристаллической решётки поваренной соли)В общеобразовательном курсе изучается прямоугольная система координат на плоскости и в пространстве. Иначе её называют Декартовой системой координат по имени французского ученого философа Рене Декарта (1596 – 1650) впервые введшего координаты в геометрию.)

4

Этап усвоения новых знаний

15

ДИДАКТИЧЕСКАЯ ЗАДАЧА – дать обучающимся конкретное представление об изучаемых фактах, явлениях, основной идее изучаемого материала; добиться от обучающихся восприятия, осознания, первичного обобщения и систематизации новых знаний, усвоения обучающимися способов, путей, средств получения знаний, оперирования ими.

Содержание:

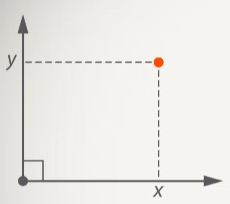
В школе шла о плоскости: у нас были две перпендикулярные оси, и каждую точку плоскости мы задавали с помощью так называемых координат, то есть величин, которые требовалось «пройти» до данной точки от начала координат. (См. Рис. 1.)

Рис. 1. Система координат на плоскости

С помощью координат было удобно решать разные задачи, но мы применяем их и в жизни. Например, в кинотеатре мы ищем свое кресло сначала по ряду, а затем по номеру в ряду. (См. Рис. 2.)

Рис. 2. Место в кинотеатре – модель координатной плоскости

Но мы живем не в двухмерном пространстве, а в трехмерном. Поэтому имеет смысл поговорить об аналоге уже привычной нам системы координат, перенеся ее в пространство.

Рассмотрим такую ситуацию. Предположим, что мы пошли не в кино, а на балет. У нас есть билет, на котором написаны ряд и место. Можем ли мы легко найти свое кресло? Да, если речь о партере. Но ведь мы можем сидеть и выше: в амфитеатре или на любом из ярусов. Поэтому в данном случае мы прибегаем к трем измерениям: сначала по высоте (ярус, амфитеатр или партер), затем уже ряд, а затем место. (См. Рис. 3.)

Рис. 3. Расположение мест в театре как пример трехмерной системы координат

Мы пользуемся координатами и тогда, когда выбираем товары в гипермаркете самообслуживания. Например, мы хотим купить стол и нам дается инструкция, что он находится в  ряду, на  полке снизу, место номер . Мы сначала ищем ряд (первая координата), затем – место (вторая), потом – полку (третья). Можно, разумеется, сначала найти полку, а потом место. Так или иначе, речь идет о трех координатах.

ДИНАМИЧЕСКАЯ ПАУЗА

5

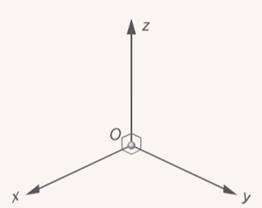
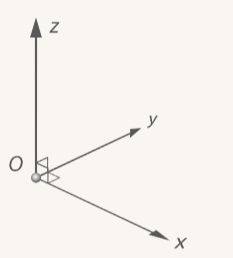
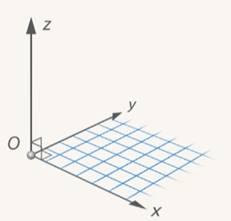
Рассмотрим произвольную точку  пространства. Проведем через нее три попарно перпендикулярные прямые. На каждой из них обозначим направление. Это и будут оси координат – теперь их стало три. Обратите внимание, что ось направлена к нам, ось  вправо, а  – вверх. Порядок здесь важен, так как такие направления образуют так называемую правую тройку. (См. Рис. 4.)

Рис. 4. Оси координат трехмерного пространства

Эту картинку можно поворачивать так, как нам удобно. Например, если мы ее повернем на  против часовой стрелки в плоскости , то получим следующую картинку:  вправо,  – вглубь,  – вверх. (См. Рис. 5.)

Рис. 5. Поворот «тройки» на  против часовой стрелки в плоскости 

Все это допустимые картинки, выбирайте любую из них. Некоторым удобна последняя, ведь она получается естественным образом из плоскостной. (См. Рис. 6.)

Рис. 6. К системе координат на плоскости добавили ось 

Рассмотрим тройку векторов , , , отложенных от одной точки . Эта тройка векторов называется правой, если векторы располагаются так, как расположены соответственно большой, указательный и средний пальцы правой руки. В противном случае тройка называется левой.

На рисунке (См. Рис. 7.) справа изображена правая тройка векторов, а слева – левая. Это также полностью соответствует правилам правой и левой руки из физики.

Рис. 7. Левая и правая тройки

Оси обозначаются  (ось абсцисс),  (ось ординат) и  (ось аппликат). (См. Рис. 8.)

Рис. 8. Названия координатных осей

Соответствующие плоскости – , ,  – координатные плоскости. (См. Рис. 9.) Как и на плоскости, у каждой оси в пространстве есть положительное направление и отрицательное.

Рис. 9. Координатные плоскости

Координаты точки в пространстве определяются аналогично плоскостным. Рассмотрим произвольную точку  и проведем через нее плоскости, параллельные координатным. Эти плоскости пересекут наши оси в точках  (точка пересечения параллельной плоскости с осью ),  (точка пересечения параллельной плоскости с осью ) и  (точка пересечения параллельной плоскости с осью ). (См. Рис. 10.)

Рис. 10. Точки пересечения параллельных плоскостей с осями координат

Тогда абсцисса точки  – это  (в случае если  лежит на положительной полуоси) и , если  – на отрицательной. (См. Рис. 11.)

Рис. 11. Абсцисса точки  в зависимости от расположения точки 

Аналогично определяются ордината и аппликата. Записывают координаты в круглых скобках через точку с запятой: , где , ,  (либо , ,  – в зависимости от расположения на осях координат). Не пишите координаты точки через запятую, чтобы не спутать с десятичными дробями.

У точки могут быть и нулевые координаты, если она лежит в координатной плоскости. Например, если взять точку в плоскости , то ее координаты имеют вид . А точка на оси  имеет координаты . Начало же координат – точка  – имеет координаты . (См. Рис. 12.)

Рис. 12. Точки с нулевыми координатами

20

5

Этап проверки понимания обучающимися материала

5

ДИДАКТИЧЕСКАЯ ЗАДАЧА – установить осмыслили ли обучающиеся связи и отношения фактов, содержание новых понятий, закономерностей, устранить обнаруженные пробелы.

Используя записи в тетради и учебник, назвать основные вопросы и формулы по данной теме

Критерий оценивания:

6

Этап закрепления нового материала

10

ДИДАКТИЧЕСКАЯ ЗАДАЧА – закрепить у обучающихся знания и умения, необходимые для самостоятельной работы по новому материалу.

Учебник Геометрия 10-11 кл Атанасян Л.С.

Критерий оценивания учащихся отвечающих у доски:

Критерий оценивания учащихся решающих на месте:

(выполнив задание, учащийся поднимает руку и показывает решение примера. В соответствии с критерием оценивания получает баллы за работу.)

7

Рефлексия учебной деятельности

3

ДИДАКТИЧЕСКАЯ ЗАДАЧА – формирование у обучающихся умения анализировать результаты своей учебной деятельности.

обсуждение и оценка результатов самостоятельной работы (рефлексия в письменной форме)

8

Этап информации обучающихся о домашнем задании, инструктаж по его выполнению:

7

ДИДАКТИЧЕСКАЯ ЗАДАЧА – подвести итоги и выставить оценки, сообщить обучающимся о домашнем задании, разъяснить методику его выполнения.

И если есть самостоятельная работа, то задания и форма контроля самостоятельной работы

90