Полный комплект
материалов
по геометрии
для 10-го класса (ФГОС)
на весь учебный год


Конечно же, это компьютер и современные технологии.
Так почему бы нам не использовать это на своих уроках?
Тратить минимум собственных сил
на подготовку и объяснения
Быстро и объективно
проверять знания ученика
Наладить дисциплину
на своих уроках
Оргмомент
Проверка домашнего задания
Используются готовые тесты
из этого проекта
Изучение нового материала
Используются видеоуроки
из этого проекта
Практика
Итоги
Тесты помогут вам проверить знания, а видеоуроки объяснят учебный материал. Это значит, вы:
Экономите
20-25 минут
на уроке
Получаете
интерес учащихся
и дисциплину
Делаете объяснения
максимально наглядными
и понятными
Имеете возможность
работать творчески
и разнообразить свои уроки
Здравствуйте. Меня зовут Дмитрий Тарасов. Я учитель, который в течение нескольких лет изучал и внедрял в свою работу современные информационные технологии. Еще в 2008 году я начал делиться накопленным опытом с коллегами в рамках проекта videouroki.net.
Сейчас над ним работает целая команда профессиональных учителей, художников, дизайнеров, программистов и дикторов.
Уже более 5 лет мы разрабатываем видеоуроки, тесты, презентации, электронные тетради и прочие полезные материалы для работы учителей.

Видеоурок —
современный наглядный
инструмент обучения
С помощью видеоурока вы можете показать то, что никогда не сможете показать на доске.
Каждый ученик получит объяснение нового материала в полном объеме без ваших лишних усилий и независимо от вашего самочувствия и настроения.
Видеоуроки помогут вам уверенно заменить отсутствующих коллег или помочь освоить урок своему собственному ребенку.
Содержит 39 видеоуроков, 21 тест и 39 презентаций
Разработан в помощь учителям математики и учащимся 10-го класса.
Ориентирован на учебник: «Геометрия. 10-11 классы» Л. С. Атанясян, cоответствует ФГОС.

*Стоимость может увеличиться уже завтра
Нажмите на кнопку, чтобы заказать проект
Оформляя заказ, вы соглашаетесь
с уcловиями лицензионного
договора

Математика во все века привлекала к себе внимание не только ученых и архитекторов, но и художников, музыкантов. На этом уроке мы окунемся в историю развития геометрии в целом и стереометрии в частности. Рассмотрим основные понятия, которые изучает стереометрия.

Изучение планиметрии мы начинали с аксиом планиметрии. В этом видеофрагменте мы рассмотрим аксиомы стереометрии, рассмотрим практическое применение аксиом стереометрии. В аксиомах стереометрии выражаются основные свойства точек, прямых и плоскостей, которые касаются их взаимного расположения.

У аксиом стереометрии есть несколько очень нужных следствий, которые упрощают решения задач и доказательства теорем. На данном уроке мы рассмотрим эти следствия и решим несколько задач, при решении которых будем использовать сами аксиомы стереометрии и следствия из них.

На этом уроке мы рассмотрим понятие параллельных прямых в пространстве. Дадим их определение. А также докажем теорему единственности прямой, параллельной данной.

В этом уроке мы продолжим рассматривать параллельные прямые в пространстве. А именно, рассмотрим параллельность трех прямых. Докажем лемму о двух параллельных прямых, пересекающих плоскость. А затем с ее помощью докажем теорему о двух прямых, параллельных третьей прямой.
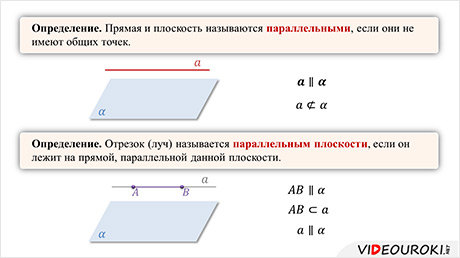
В этом видеофрагменте мы рассмотрим параллельность прямой и плоскости как один из трех возможных вариантов их взаимного расположения в пространстве. Сформулируем и докажем теорему о параллельности прямой и плоскости. А также докажем еще два утверждения, которые часто применяют при решении задач.

На данном уроке мы дадим определение скрещивающихся прямых. Рассмотрим возможные случаи взаимного расположения двух прямых в пространстве. Докажем теорему, которая выражает признак скрещивающихся прямых. А также докажем теорему о том, что через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.

В этом уроке мы введем понятие сонаправленных лучей. Дадим их определение. А затем докажем теорему о равенстве углов с сонаправленными сторонами.

В данном видеофрагменте мы рассмотрим углы между пересекающимися и скрещивающимися прямыми. А также решим несколько задач на нахождение скрещивающихся углов.

На этом уроке мы узнаем, какие плоскости называются параллельными в пространстве. А также сформулируем и докажем теорему, которая выражает признак параллельности плоскостей.

В данном уроке мы рассмотрим некоторые из свойств, которыми обладают две параллельные плоскости в пространстве. А точнее, узнаем, что если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Докажем, что отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. А также докажем свойство о существовании единственной плоскости, параллельной данной плоскости и проходящей через точку вне ее.
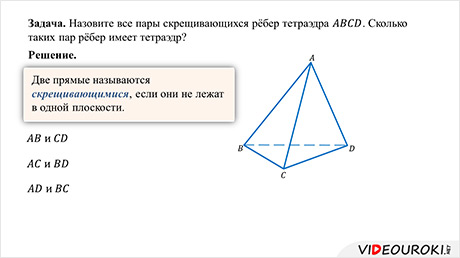
В начале изучения курса «Стереометрии» мы говорили, что все геометрические тела делятся на тела вращения и многогранники. В процессе изучения геометрии в десятом классе мы будем подробно рассматривать с вами свойства тех или иных фигур. В этом видеофрагменте мы познакомимся с такой фигурой, как тетраэдр. Познакомимся с основными элементами тетраэдра. Решим несколько задач по этой теме.
С параллелепипедом мы уже знакомы. Напомним, что в курсе геометрии базовой школы мы определяли параллелепипед как четырехугольную призму, основаниями которой являются параллелограммы. На этом уроке мы дадим немного другое определение параллелограмма. Повторим основные элементы параллелепипеда, решим несколько задач.

Очень часто при решении задач необходимо строить сечение тех или иных пространственных фигур. В этом видеофрагменте мы введем понятие сечения тетраэдра и параллелепипеда. Рассмотрим, какие фигуры могут получиться при сечении тетраэдра и параллелепипеда плоскостью. Разберем задачи на построение сечений тетраэдра и параллелепипеда.

На этом уроке вводится определение перпендикулярных прямых в пространстве. А также доказывается лемма о двух параллельных прямых, перпендикулярных к третьей прямой. Рассматриваются случаи перпендикулярных прямых, которые пересекаются и скрещиваются.
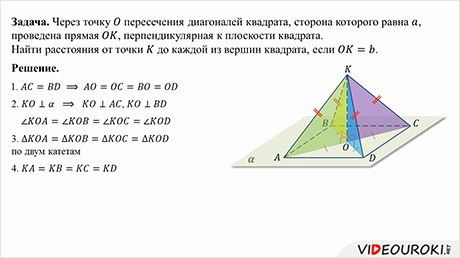
Этот урок знакомит с определением прямой перпендикулярной к плоскости, после чего рассматриваются примеры решения задач с применением этого определения. Кроме того, доказываются прямая и обратная теоремы о параллельных прямых, перпендикулярных к плоскости, которые находят своё применение в решении геометрических задач.
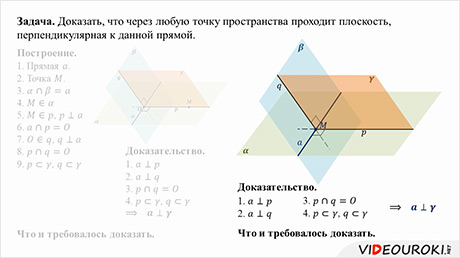
Знать определение прямой перпендикулярной к плоскости зачастую недостаточно для успешного решения задач. Поэтому на этом уроке учащиеся знакомятся с признаком перпендикулярности прямой и плоскости. Пополнив таким образом свой багаж знаний, ученики смогут значительно расширить круг решаемых задач.
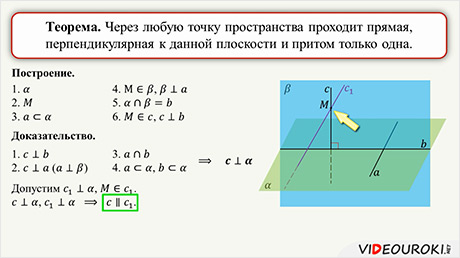
После изучения признака перпендикулярности прямой и плоскости, переходим к знакомству с теоремой о прямой, перпендикулярной к плоскости. После этого урока учащиеся будут владеть всем набором знаний о перпендикулярности прямой и плоскости.
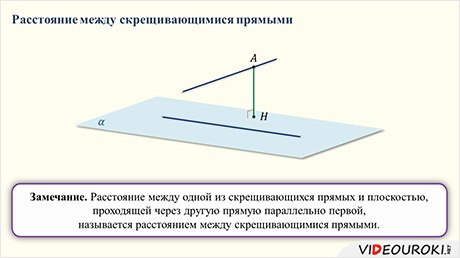
На этом уроке учащиеся узнают, как находить расстояние от точки до плоскости, расстояние между двумя параллельными плоскостями, расстояние между прямой и параллельной ей плоскостью, а также расстояние между скрещивающимися прямыми.
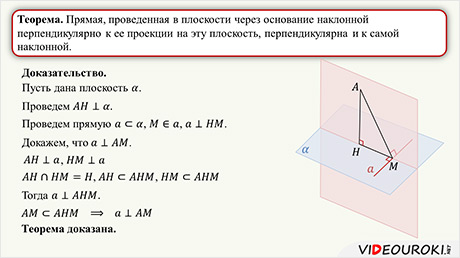
В этом видеофрагменте мы сформулируем теорему о трех перпендикулярах и докажем ее. Сформулируем и докажем обратную ей теорему. А также решим несколько задач на применение теоремы о трех перпендикулярах.
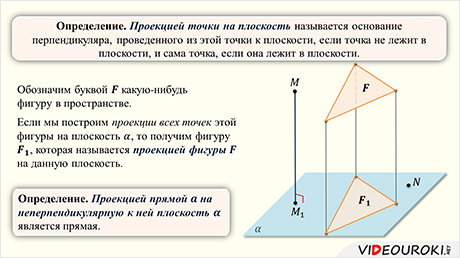
В этом уроке мы введем понятие проекции произвольной фигуры. Дадим определение проекции точки на плоскость. А затем сформулируем представление об угле между прямой и плоскостью.
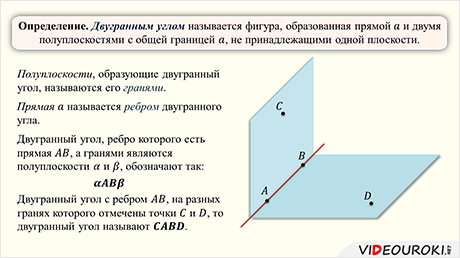
На этом уроке мы познакомимся с таким понятием, как двугранный угол. А также узнаем о том, как определить линейный угол рассматриваемой геометрической фигуры. А также убедимся, что градусной мерой двугранного угла называется градусная мера его линейного угла и что все линейные углы двугранного угла равны между собой.
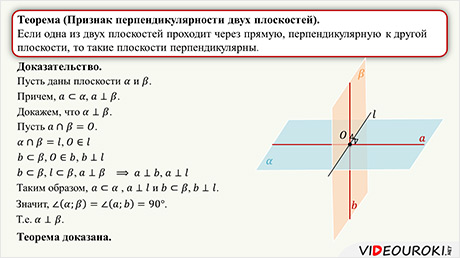
В данном видеофрагменте мы рассмотрим, какие плоскости называются перпендикулярными. Сформулируем и докажем признак перпендикулярности двух плоскостей. А также выведем и докажем некоторые следствия.

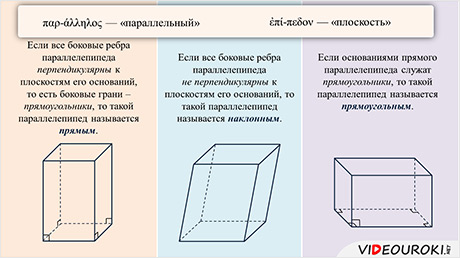
Когда мы изучали тему «Параллелепипед», мы говорили, что если все боковые ребра параллелепипеда перпендикулярны к плоскостям его оснований, т. е. боковые грани – прямоугольники, то такой параллелепипед называется прямым. Если же и основаниями прямого параллелепипеда служат прямоугольники, то такой параллелепипед называется прямоугольным.
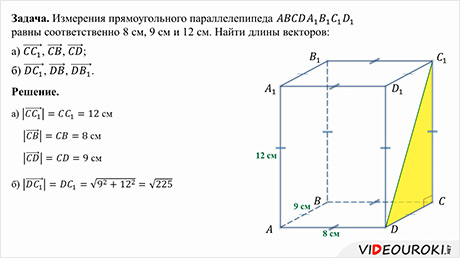
На этом уроке мы познакомимся с прямоугольным параллелепипедом поближе. Введем такое понятие, как «измерения прямоугольного параллелепипеда», рассмотрим свойства прямоугольного параллелепипеда.
Тема видеофрагмента «Понятие многогранника». Начиная изучать стереометрию, мы говорили, что все геометрические тела делятся на два больших класса: тела вращения и многогранники, с некоторыми многогранниками мы с вами уже знакомы.
Этот урок открывает раздел, в котором мы познакомимся с другими многогранниками, но прежде давайте вспомним основные понятия, связанные с многогранниками.
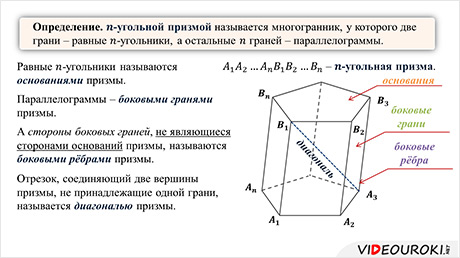
В курсе геометрии базовой школы мы уже знакомились с такими многогранниками, как призмы. Целями нашего урока будут: повторить основные понятия, связанные с призмами; рассмотреть виды призм; вывести формулу для вычисления площади боковой поверхности прямой и наклонной призм.
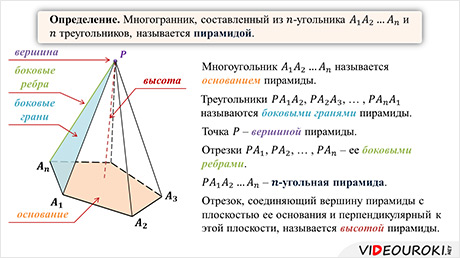
В курсе геометрии базовой школы мы уже знакомились с такими многогранниками, как пирамиды. В этом видеофрагменте мы повторим основные понятия, связанные с пирамидами, рассмотрим правильные пирамиды, их свойства.
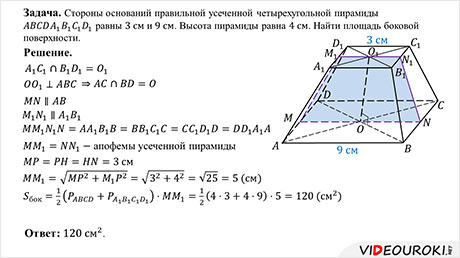
Вокруг нас много примеров усеченных пирамид. Например, вытяжка над кухонной плитой имеет форму усеченной пирамиды, клавиши клавиатуры и другие предметы. В этом видеофрагменте мы подробно рассмотрим такую фигуру, как усеченная пирамида: как она получается, какими свойствами обладает. Отдельно рассмотрим правильную усеченную пирамиду, ее свойства.
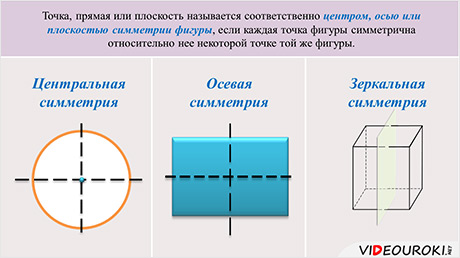
Тема урока «Симметрия в пространстве». Симметрия – один из законов, обеспечивающих гармонию вселенной. Именно о симметрии мы сегодня и поговорим. Мы вспомним, какие фигуры мы называли симметричными относительно прямой и точки. Дадим новые определения таким симметриям. Введем понятие симметрии относительно плоскости.
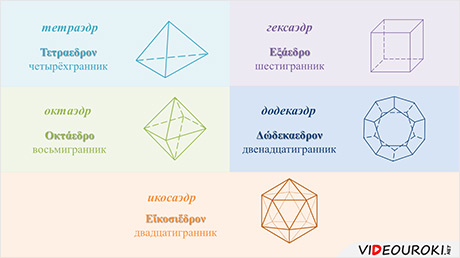
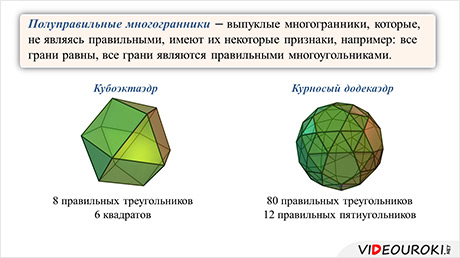
На этом уроке мы познакомимся с понятием правильного многогранника. Выявим, что существуют только пять видов правильных многогранников: тетраэдр, гексаэдр (или куб), октаэдр, икосаэдр и додекаэдр. А также рассмотрим каждый из них.
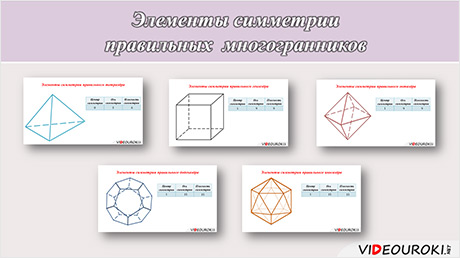
В этом видеофрагменте мы повторим, какие же многогранники называются правильными, рассмотрим элементы симметрии правильных многогранников, попробуем их подсчитать.
Понятие вектора известно ещё из курса планиметрии. Но при изучении стереометрии векторы рассматриваются уже не на плоскости, а в пространстве. Понятие вектора, определение коллинеарных (сонаправленных и противоположно направленных) векторов в пространстве вводится аналогично тому, как это делали на плоскости. В ходе решения задач учащиеся смогут в этом убедиться.
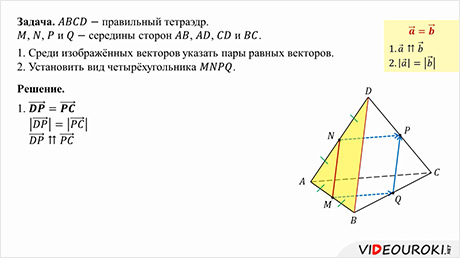
На этом уроке учащиеся вспомнят определение равных векторов на плоскости и сформулируют такое же для векторов в пространстве. При решении задач рассматриваются многочисленные многогранники, которые и помогают усвоению знаний о равных векторах в пространстве.
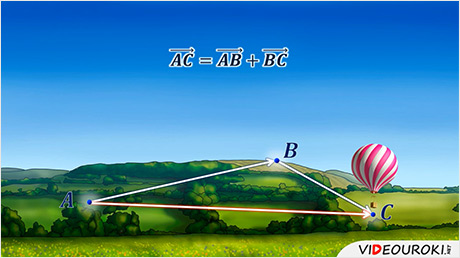
В пространстве сложение и вычитание векторов выполняют в точности так же, как и на плоскости. На этом уроке учащиеся вспомнят правила треугольника и параллелограмма сложения двух векторов, теорему о разности двух векторов, и применят эти знания при решении пространственных задач.
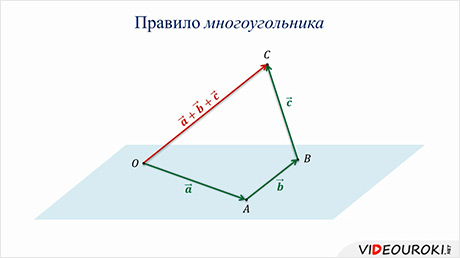
На этом уроке учащиеся впервые увидят отличие векторов в пространстве и на плоскости при построении многоугольника сложения нескольких векторов. В пространстве многоугольник сложения может быть пространственным, то есть не все его вершины лежат в одной плоскости.
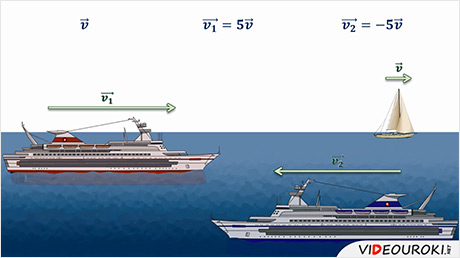
Уже стало привычным, что действия над векторами в пространстве выполняются так же, как и на плоскости (за исключением сложения нескольких векторов). На этом уроке аналогично тому, как это было на плоскости, вводится определение произведения вектора на число.
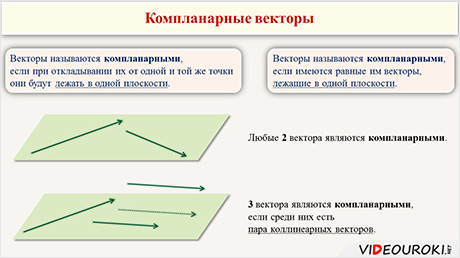
Первое понятие о векторах в пространстве, которого не было на плоскости — компланарность векторов. С определения компланарных векторов и начинаются главные отличия векторов в планиметрии и стереометрии. При рассмотрении примеров решений задач учащиеся усвоят понятие компланарности, что позволит успешно продолжить изучение векторов.
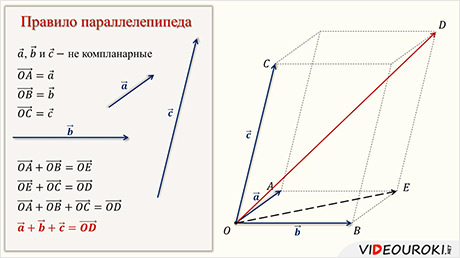
На этом уроке вводится правило параллелепипеда сложения трёх некомпланарных векторов и рассматриваются примеры его применения при решении различных задач.

В ходе этого урока учащиеся узнают, что любой вектор пространства можно разложить по трём некомпланарным векторам. При решении задач они приобретут навык такого разложения и смогут без труда определять его коэффициенты.
Компьютерные тесты — инструмент быстрой и объективной проверки знаний
Компьютерное тестирование поможет вам за 5 минут быстро и объективно проверить знания всех учащихся класса.
Готовые тесты для распечатки помогут вам сэкономить время при подготовке к уроку, если у вас в кабинете нет возможности использовать компьютер.
39 готовых презентаций — помогут вам самостоятельно объяснить учебный материал
Иногда, даже если у вас есть готовый видеоурок, хочется объяснить материал самому. В этом вам помогут презентации.
Эти презентации с готовыми иллюстрациями и определениями вы можете изменять так, как вам нравится, и использовать при своих объяснениях.

Фронтально
с помощью проектора

В компьютерном классе
по сети

На компьютере
или ноутбуке
Оформите заказ до 25.02.2026 и получите онлайн-версию в подарок.
Создавайте классы и добавляйте в них учеников, используя личный кабинет учителя. Раздавайте учащимся видеоуроки и тесты из этого комплекта в их личные кабинеты, сообщив им пароли для входа. Ученики, зайдя в свои кабинеты, выполняют работу, а вы видите все их действия и результаты в деталях, что позволяет вам полностью управлять процессом обучения.
Раздавайте видеоуроки и конспекты из этого комплекта в личные кабинеты учеников как на уроке, так и дистанционно. Ученики приступают к просмотру, а вам остаётся лишь следить за статистикой в реальном времени. Благодаря ей вы будете на 100 % уверены, что ученик смотрел видео, не отвлекаясь на другие дела.
Раздайте тесты из этого комплекта в личные кабинеты ученикам и полностью контролируйте их работу. Используя настройки теста, вы можете ограничить учащимся количество попыток его выполнения и промежуток времени, в который тест будет доступен для выполнения, а также изменить настройку, показывать или нет ошибки и решения по окончании теста. Вся информация о прохождении теста классом собирается в удобную таблицу.
Видеоуроки
Тесты
Презентации
Продуктивные интересные уроки, ваше свободное время, репутация современного учителя, возможность работать творчески, дисциплина на уроке, экономия ваших сил и энергии, наглядное и понятное обучение.

Нажмите сюда, чтобы заказать проект
Оформляя заказ, вы соглашаетесь с уcловиями лицензионного договора

Тема «Многогранники», наравне с темой «Тела вращения», занимает важное место в изучении стереометрии. Основная часть многогранников рассматривается в курсе геометрии 10 класса. Именно поэтому мы собрали все известные нам сведения о многогранниках в одном справочнике.
На поиск нужных формул, определений, свойств тех или иных фигур ученики тратят большое количество времени как на уроках, так и дома. Но теперь Вам и Вашим ученикам не придётся тратить время на поиски нужного материала по теме «Многогранники», перелистывая страницы учебника, – он уже собран в одном документе!
Данный справочный материал пригодится не только на уроках, но и в будущем при подготовке к школьным экзаменам.
Справочник «Многогранники» очень удобно использовать в электронном виде, а также, распечатав материалы справочника, у Вас в руках окажется незаменимый раздаточный материал, который поможет сделать Ваши уроки еще более эффективными.

Для работы с компьютерными тестами вам понадобится специальная программа. Она бесплатна и работает как в Windows, так и в Linux.
Но, для того, чтобы вам не пришлось самостоятельно разбираться во всех тонкостях её работы, мы подарим вам специальный видеокурс, который поможет вам освоить компьютерное тестирование за 5 минут.
Вы не только сможете использовать подготовленные нами тесты из этого проекта, но также научитесь создавать свои собственные и редактировать уже имеющиеся.
Понятно, что при заказе через Интернет всегда есть сомнения в честности того, кто находится по ту
сторону экрана.
В этом случае вы можете полностью нам доверять, потому что:

Я не первый раз заказываю у Вас диски, они о-о-очень помогают мне в работе
Уважаемый Дмитрий! Вы меня благодарите - это Вас надо благодарить за этот титанический труд. Я не первый раз заказываю у Вас диски, они о-очень помогают мне в работе. Вы и сами прекрасно понимаете, как Ваши уроки сокращают всем время на подготовку. Вам спасибо за все и желаю Вам творческих и профессиональных успехов. Удачи!

Даже «тупенькие» что-то воспринимают
Дмитрий, пользуюсь Вашими проектами в полной мере. Есть классы, в которых одно и тоже говори каждый урок, и для них это будет "как в первый раз", очень обидно и жалко свой труд. Поставил урок: "это мы видели в прошлый раз", радует - запомнили! Повторять не надо!. Даже "тупенькие" что-то воспринимают: ведь стыдно, не понять то, о чем говорилось в прошлый урок!
Содержание диска очень понравилось. Хотелось бы еще и 8 класс иметь в таком варианте
Здравствуйте, Дмитрий. Спасибо за оперативность, диск получила достаточно быстро. Содержание диска очень понравилось. хотелось бы еще и 8 класс иметь в таком варианте. ваш труд неоценим особенно для учителей малокомплектных школ, когда помимо основного предмета приходится самостоятельно осваивать дополнительные.

У меня есть все диски которые Вы создали. Это огромная помощь учителю.
Дмитрий, добрый день!Я очень Вам благодарна за все, что вы делаете. У меня есть все диски которые Вы создали. Это огромная помощь учителю. Все очень доступно объяснено. Не представляю, когда Вы все успеваете. Желаю Вам творческих успехов и огромные слова благодарности! СПАСИБО!!!!
Для получения этого проекта нажмите кнопку оформить заказ и введите свои данные для получения материалов. Далее вы можете оплатить свой заказ онлайн или по квитанции и получить ссылку для скачивания комплекта сразу после отслеживания нами оплаты (для электронных систем мгновенно, при оплате по квитанции 1-3 дня).
Да, если вы заказываете материал и делаете его предоплату, то вы дополнительно получите письмо со ссылкой для скачивания электронной версии данного проекта. Оно будет выслано автоматически, сразу после прохождения оплаты.
Все наши разработки на русском языке.
Мы предлагаем свои проекты для учителей, для их персонального использования в работе. Это значит, что вы можете пользоваться ими и установить их материалы и программы на все компьютеры в своем учебном классе. Но ваши коллеги уже должны покупать для своей работы отдельные лицензии.
Также запрещается копировать, тиражировать и распространять этот проект или его части всевозможными способами ни учителям, ни домой ученикам, ни любым иным третьим лицам, т.к. это будет противоречить лицензионному соглашению.
Т.е. на сегодняшний день данная лицензия привязывается к вам как к конкретному человеку.
Эти проекты помогают в обучении и работе учителя, как стиральная
машина при стирке, как микроволновая печь при разогреве,
как автомобиль при перемещении.
Это не просто готовые видеоуроки и тесты, это ваше свободное
время, удобство и комфорт. Закрыв эту страницу, вы вряд ли снова
попадете сюда, а значит рискуете так никогда и не получить
возможность работать и жить по-новому, более свободно, интересно
и продуктивно.

*Стоимость может увеличиться уже завтра
Нажмите сюда, чтобы заказать проект
Оформляя заказ, вы соглашаетесь с уcловиями лицензионного договора
Задать вопрос в службу поддержки
Электронная почта [email protected]
Мы работаем:
в будние дни с 8:00 до 17:00 (МСК)